22.Выводить формулы, использующие понятие определенного интеграла для его геометрических и механических приложений.

Геометрический смысл определенного интеграла. Если f(x) непрерывна и положительна на [a, b], то интеграл

представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f(x) (см. рис. 5.).

Не следует думать, что условие непрерывности функции необходимо для того, чтобы у нее существовал определенный интеграл. Интеграл может существовать и у разрывной функции. Пусть, например, функция f(x), заданная на промежутке [a, b], равна нулю во всех точках этого промежутка, кроме конечного числа точек z₁, z₂, ..., z_N. Составим для f(x) интегральную сумму σ.

Пусть из точек ξ₀, ξ₁, ..., ξ_n-1, входящих в определение σ, p точек совпадают с точками z_i, а остальные отличны от них. Тогда в сумме σ будет лишь p слагаемых, отличных от нуля. Если наибольшее из чисел | f(z_i) | (i = 1, 2, ..., N) есть K, то, очевидно,

| σ | ≤ Kpλ ≤ KNλ,

откуда ясно, что при λ → 0 будет и σ → 0. Таким образом, интеграл

существует и равен нулю.

     Приведем теперь пример функции, не имеющей интеграла. Пусть φ(x) задана на промежутке [0, 1] так:

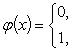
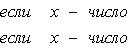
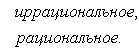
Если мы, составляя сумму σ, за точки ξ_k выберем числа иррациональные, то окажется σ = 0. Если же все ξ_k взять рациональными, то получится σ = 1. Таким образом, за счет одного лишь уменьшения λ нельзя приблизить σ к какому-либо постоянному числу, и интеграл

не существует.

Механический смысл определенного интеграла.

Опираясь на механический смысл неопределенного интеграла по формуле Ньютона-Лейбница соответственно получим:

, (52)

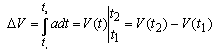(53)

То есть с позиции механики определенный интеграл от скорости прямолинейно движущейся точки есть изменение ее расстояния   от фиксированного положения за известный промежуток времени  , определенный интеграл от ее ускорения есть изменение ее скорости за рассматриваемый промежуток времени 

27.Знать определение предела и непрерывности функции двух переменных

 Предел функции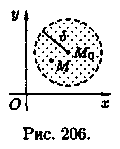

Для функции двух (и большего числа) переменных вводится понятие предела функции и непрерывности, аналогично случаю функции одной переменной. Введем понятие окрестности точки. Множество всех точек М(х;у) плоскости, координаты которых удовлетворяют неравенству называется -окрестностью точки М₀(х₀;у₀). Другими словами, -окрестность точки М_о — это все внутренние точки круга с центром М_о и радиусом 8 (см. рис. 206).

Пусть функция z = ƒ(х; у) определена в некоторой окрестности точки М₀(х₀;у₀), кроме, быть может, самой этой точки. Число А называется пределом функции z = ƒ (х; у) при х → х₀ и у → у₀ (или, что то же самое, при М(х; у) → М₀(х₀; у₀)), если для любого є > 0 существует  > 0 такое, что для всех х ≠ х₀ и у ≠ у₀ и удовлетворяющих неравенству

 выполняется неравенство | ƒ (х; у) — А| < є. Записывают:

Из определения следует, что если предел существует, то он не зависит от пути, по которому М стремится к М_о (число таких направлений бесконечно; для функции одной переменной х → х₀ по двум направлениям: справа и слева!)

Геометрический смысл предела функции двух переменных состоит в следующем. Каково бы ни было число є>0, найдется -окрестность точки M_о(х_о;у_о), что во всех ее точках М(х;у), отличных от М_о, аппликаты соответствующих точек поверхности z=ƒ(х;у) отличаются от числа А по модулю меньше, чем на є.

Пример 43.1. Найти предел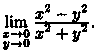

Решение: Будем приближаться к О(0;0) по прямой у=Кх, где К — некоторое число. Тогда

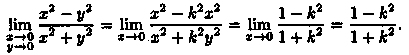
Функция   в точке О(0; 0) предела не имеет, т. к. при разных значенияхК предел функции не одинаков (функция имеет различные предельные значения).

 

Предел функции двух переменных обладает свойствами, аналогичными свойствам предела функции одной переменной (см. п. 17.3). Это означает, что справедливы утверждения: если функции ƒ (М) и g(М) определены на множестве D и имеют в точке М_о этого множества пределы А и В соответственно, то и функции ƒ(М) ± g(M), ƒ(М) • g(М), имеют в точке Мо пределы, которые соответственно равны А ± В, А • В, ^A/_B(В≠0).

 

43.3. Непрерывность функции двух переменных

Функция z = ƒ(х;у) (или ƒ(М)) называется непрерывной в точке М₀(х₀;у₀), если она:

а) определена в этой точке и некоторой ее окрестности,

б) имеет предел

в) этот предел равен значению функции z в точке М_о, т. е.

Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Точки, в которых непрерывность нарушается (не выполняется хотя бы одно из условий непрерывности функции в точке), называются точками разрыва этой функции. Точки разрыва z=ƒ(х;у) могут образовывать целые линии разрыва. Так, функция   имеет линию разрыва у=х.

Можно дать другое, равносильное приведенному выше, определение непрерывности функции z=ƒ(х;у) в точке. Обозначим Δх=х—х_0, Δу=у—у₀, Δz=ƒ(х;у)—ƒ(х₀;у₀). Величины Δх и Δу называются приращениями аргументов х и у, а Δz — полным приращением функции ƒ(х;у) в точке М₀(х₀;у₀).

Функция z = ƒ(х;у) называется непрерывной в точке М₀(х₀;у₀) є D, если выполняется равенство т. е. полное приращение функции в этой точке стремится к нулю, когда приращения ее аргументов х и у стремятся к нулю.

Пользуясь определением непрерывности и теоремами о пределах, можно доказать, что арифметические операции над непрерывными функциями и построение сложной функции из непрерывных функций приводит к непрерывным функциям — подобные теоремы имели место для функций одной переменной (см. п. 19.4).