
- •11.Знать определение простейшей рациональной дроби и уметь представлять правильную рациональную дробь в виде суммы простейших дробей
- •12.Знать определение первообразной и доказывать теорему, что две первообразные одной и той же функции отличаются на постоянную
- •13.Доказывать основные свойства неопределённого интеграла
- •14. Выводить формулы замены переменной и интегрирования по частям для неопределенного интеграла
- •Интегрирование по частям
- •15.Выводить формулы интегрирования простейших рациональных дробей
- •16. Излагать приёмы вычисления интегралов вида:
- •17.Знать определение определенного интеграла. Формулировать теорему существования определенного интеграла.
- •18.Доказывать основные свойства определенного интеграла
- •19. Доказывать теорему о среднем.
- •20.Доказывать теорему о производной определенного интеграла по переменному верхнему пределу и выводить формулу Ньютона–Лейбница
- •21.Выводить формулы замены переменной и интегрирования по частям для определенного интеграла
- •22.Выводить формулы, использующие понятие определенного интеграла для его геометрических и механических приложений.
- •27.Знать определение предела и непрерывности функции двух переменных
- •28.Сформулировать свойства функции, непрерывной в замкнутой ограниченной области
- •29.Знать определение частных производных. Уметь выводить формулы производной сложной функции двух переменных, полной производной, производной неявной функции
- •30.Знать определение дифференцируемости функции, доказывать теоремы о необходимом условии дифференцируемости, о достаточном условии дифференцируемости
- •33. Формула касательной к плоскости и нормали
- •34.Необходимые условия экстремума
- •35. Достаточное условие экстремума
- •35. Достаточное условие экстремума (2 вариант)
- •39. Знать определения криволинейных интегралов первого и второго рода и уметь их вычислять
- •41.Знать формулы Грина
20.Доказывать теорему о производной определенного интеграла по переменному верхнему пределу и выводить формулу Ньютона–Лейбница

Формула Ньютона–Лейбница
Пусть f (x) произвольная непрерывная на отрезке [a, b] функция и пусть F (x) какая-нибудь её первообразная. Разобьём отрезок [a, b] на n частей и составим разность
F ( b ) - F ( a )
значений первообразной на концах интервала [a, b]. Эта разность равна сумме разностей, составленных для каждого отрезка разбиения,
![]()
По теореме Лагранжа о "конечном приращении" имеем
![]() ,
,
поэтому
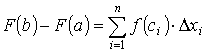 .
.
Это равенство является точным при любом разбиении отрезка [a, b], но оно справедливо лишь при определённом выборе на каждом отрезке разбиения точек
c1 < c2 < … < cn,
которые предписывается теоремой Лагранжа. Если размеры всех отрезков разбиения
[а = х0, x1], [х1, x2],…, [х n - 1, b]
будут становиться всё меньше и меньше, то сумма
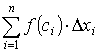
будет являться суммой возрастающего числа стремящихся к нулю слагаемых. Если равенство
верно всегда, то оно верно и в пределе:
 .
.
Полученное равенство замечательно тем, что оно справедливо не только при каком-то частном выборе точек
c1 < c2 < … < cn
по одной на отрезках деления
[а = х0, x1], [х1, x2],…, [х n - 1, b]
как это предписывается теоремой Лагранжа, но при всяком выборе точек ξ 1 < ξ 2, <… < ξ n по одной на отрезках деления [а = х0, x1], [х1, x2],…,[хn - 1, b]:
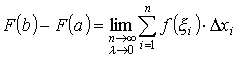 .
.
Последнее соотношение является замечательным правилом суммирования бесконечно малых, открытых Лейбницем и Ньютоном: для отыскания предела суммы бесконечно малых
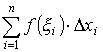 ,
,
когда все отрезки, на которые разбит отрезок [a, b], безгранично умаляются, необходимо выполнить два действия:
1) постараться отыскать конечным образом какую-нибудь первообразную F(х) для функции f (x);
2) найдя первообразную F(х), составить разность F(b) - F(a) её значений на концах основного отрезка [a, b]. Эта разность и есть искомый предел.
Сопоставляя это правило с определением определённого интеграла, получим формулу Ньютона—Лейбница
 .
.
При применении формулы Ньютона-Лейбница несущественно, какой из пределов интегрирования больше: верхний или нижний.
21.Выводить формулы замены переменной и интегрирования по частям для определенного интеграла
Замена переменной в определённом интеграле
Пусть функция φ (t) имеет непрерывную производную на отрезке [α, β], а = φ (α), b = φ (β) и функция f (x) непрерывна в каждой точке x = φ (t), где t [α, β]. Тогда справедливо равенство
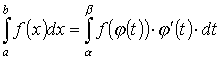
Действительно, пусть F(x) и Ф(t) — некоторые первообразные для функций f ( x) и f (φ (t))·φ ' (t). Доказано, что F (φ (t)) также является первообразной для функции f (φ (t))·φ ' (t). Тогда найдется такое число С, что Ф(t) = F(φ (t)) + C, где t [ α, β]. Поэтому
Ф(β) - Ф(α) = F(φ (β)) + C - (F(φ (α)) + C) = F(b) - F(a).
Использование замены переменной позволяет упростить интеграл, приблизив его к «табличному». При этом в отличие от неопределенного интеграла, в данном случае нет необходимости возвращаться к исходной переменной интегрирования. Достаточно лишь найти пределы интегрирования α и β по новой переменной t как решение относительно переменной t из уравнений φ (t) = a и φ (t) = b.
Формула интегрирования по частям для определённого интеграла.
Если u(x), v(x) -
непрерывно дифференцируемые функции,
то 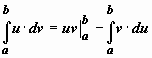 .
Док-во.
Интегрируем равенство
.
Док-во.
Интегрируем равенство ![]() в
пределах от a до b:
в
пределах от a до b: 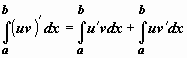 Функция в левом интеграле имеет
первообразную uv,
по формуле Ньютона-Лейбница
Функция в левом интеграле имеет
первообразную uv,
по формуле Ньютона-Лейбница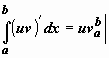 ,
следовательно,
,
следовательно, 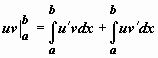 ,
откуда и следует доказываемое равенство.
,
откуда и следует доказываемое равенство.
