
- •11.Знать определение простейшей рациональной дроби и уметь представлять правильную рациональную дробь в виде суммы простейших дробей
- •12.Знать определение первообразной и доказывать теорему, что две первообразные одной и той же функции отличаются на постоянную
- •13.Доказывать основные свойства неопределённого интеграла
- •14. Выводить формулы замены переменной и интегрирования по частям для неопределенного интеграла
- •Интегрирование по частям
- •15.Выводить формулы интегрирования простейших рациональных дробей
- •16. Излагать приёмы вычисления интегралов вида:
- •17.Знать определение определенного интеграла. Формулировать теорему существования определенного интеграла.
- •18.Доказывать основные свойства определенного интеграла
- •19. Доказывать теорему о среднем.
- •20.Доказывать теорему о производной определенного интеграла по переменному верхнему пределу и выводить формулу Ньютона–Лейбница
- •21.Выводить формулы замены переменной и интегрирования по частям для определенного интеграла
- •22.Выводить формулы, использующие понятие определенного интеграла для его геометрических и механических приложений.
- •27.Знать определение предела и непрерывности функции двух переменных
- •28.Сформулировать свойства функции, непрерывной в замкнутой ограниченной области
- •29.Знать определение частных производных. Уметь выводить формулы производной сложной функции двух переменных, полной производной, производной неявной функции
- •30.Знать определение дифференцируемости функции, доказывать теоремы о необходимом условии дифференцируемости, о достаточном условии дифференцируемости
- •33. Формула касательной к плоскости и нормали
- •34.Необходимые условия экстремума
- •35. Достаточное условие экстремума
- •35. Достаточное условие экстремума (2 вариант)
- •39. Знать определения криволинейных интегралов первого и второго рода и уметь их вычислять
- •41.Знать формулы Грина
15.Выводить формулы интегрирования простейших рациональных дробей

Разложение рациональной дроби на сумму простейших дробей.
Запишем рациональную функцию в следующем виде:

Общее число неопределенных коэффициентов Ai , Bi , Ki , Li , Mi , Ni , ... должно быть равно степени знаменателя Q(x). Затем умножим обе части полученного уравнения на знаменатель Q(x) и приравняем коэффициенты при слагаемых с одинаковыми степенями x. В результате мы получим систему линейных уравнений относительно неизвестных коэффициентов Ai , Bi , Ki , Li , Mi , Ni , .... Данная система всегда имеет единственное решение. Описанный алгоритм представляет собой метод неопределенных коэффициентов.
16. Излагать приёмы вычисления интегралов вида:

17.Знать определение определенного интеграла. Формулировать теорему существования определенного интеграла.
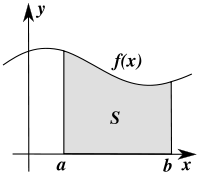
Определение.
Определённый
интеграл  численно
равен площади фигуры, ограниченной осью
абсцисс, прямыми
численно
равен площади фигуры, ограниченной осью
абсцисс, прямыми ![]() и
и ![]() и
графиком функции
и
графиком функции ![]() .
.
Пусть
определена
на ![]() .
Разобьём
на
части с несколькими произвольными
точками
.
Разобьём
на
части с несколькими произвольными
точками ![]() Тогда
говорят, что произведено
разбиение
Тогда
говорят, что произведено
разбиение ![]() отрезка
Далее
выберем произв. точку
отрезка
Далее
выберем произв. точку ![]() ,
, ![]() ,
,
Определённым
интегралом от функции
на
отрезке
называется
предел интегральных сумм при стремлении
ранга разбиения к нулю ![]() ,
если он существует независимо от
разбиения
и
выбора точек
,
если он существует независимо от
разбиения
и
выбора точек ![]() ,
т.е.
,
т.е.

Если существует указанный предел, то функция называется интегрируемой на по Риману.
Теорема существования определённого интеграла.
Если
функция f(x) непрерывна
на отрезке [a,b],
то она интегрируема по этому отрезку.
Примем
это утверждение без доказательства,
поясним только его смысл. Интегрируемость
функции означает существование конечного
предела последовательности интегральных
сумм, т.е. такого числа 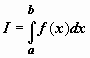 ,
что для любого
,
что для любого ![]() найдётся
такое число
найдётся
такое число ![]() ,
что как только разбиение отрезка
удовлетворяет неравенству
,
что как только разбиение отрезка
удовлетворяет неравенству ![]() ,
то, независимо от выбора точек
,
то, независимо от выбора точек ![]() выполняется
неравенство
выполняется
неравенство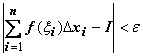 .
Требование непрерывности f(x) достаточно
для интегрируемости, но не является
необходимым. Интегрируемы функции,
имеющие конечное или даже счётное число
точек разрыва на [a,b] при
условии их ограниченности (т.е. все точки
разрыва должны быть точками разрыва
первого рода). Неограниченная функция
не может быть интегрируемой (идея
доказательства этого утверждения:
если f(x) неограничена
на [a,b],
то она неограничена на каком-либо [xi-1
, xi],
т.е. на этом отрезке можно найти такую
точку
,
что слагаемое
.
Требование непрерывности f(x) достаточно
для интегрируемости, но не является
необходимым. Интегрируемы функции,
имеющие конечное или даже счётное число
точек разрыва на [a,b] при
условии их ограниченности (т.е. все точки
разрыва должны быть точками разрыва
первого рода). Неограниченная функция
не может быть интегрируемой (идея
доказательства этого утверждения:
если f(x) неограничена
на [a,b],
то она неограничена на каком-либо [xi-1
, xi],
т.е. на этом отрезке можно найти такую
точку
,
что слагаемое ![]() ,
а следовательно, и вся интегральная
сумма, будет больше любого наперед
заданного числа).
,
а следовательно, и вся интегральная
сумма, будет больше любого наперед
заданного числа).
Обозначения.
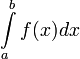
 –
нижний
предел.
–
нижний
предел.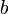 –
верхний
предел.
–
верхний
предел.– подынтегральная функция.
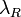 -
длина частичного отрезка.
-
длина частичного отрезка.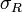 –
интегральная
сумма от функции
на
соответствующей
разбиению
.
–
интегральная
сумма от функции
на
соответствующей
разбиению
.- максимальная длина част. отрезка.
18.Доказывать основные свойства определенного интеграла


19. Доказывать теорему о среднем.
Теорема о среднем.
Если f(x) непрерывна
на отрезке [a,b],
то существует точка ![]() ,
такая что
,
такая что  .
.
![]() Док-во.
Функция, непрерывная на отрезке, принимает
на этом отрезке своё наименьшее m и
наибольшее M значения.
Док-во.
Функция, непрерывная на отрезке, принимает
на этом отрезке своё наименьшее m и
наибольшее M значения.  Тогда
Тогда 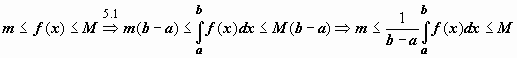 .
Число
.
Число 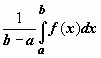 заключено
между минимальным и максимальным
значениями функции на отрезке. Одно из
свойств функции, непрерывной на отрезке,
заключается в том, что эта функция
принимает любое значение, расположенное
между mи M.
Таким образом, существует точка
,
такая что
заключено
между минимальным и максимальным
значениями функции на отрезке. Одно из
свойств функции, непрерывной на отрезке,
заключается в том, что эта функция
принимает любое значение, расположенное
между mи M.
Таким образом, существует точка
,
такая что 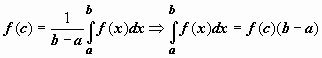 .
Это
свойство имеет простую геометрическую
интерпретацию: если
.
Это
свойство имеет простую геометрическую
интерпретацию: если ![]() непрерывна
на отрезке [a,b],
то существует точка
такая,
что площадь криволинейной трапеции ABCD равна
площади прямоугольника с основанием [a,b] и
высотой f(c) (на
рисунке выделен цветом).
непрерывна
на отрезке [a,b],
то существует точка
такая,
что площадь криволинейной трапеции ABCD равна
площади прямоугольника с основанием [a,b] и
высотой f(c) (на
рисунке выделен цветом).
