Оглавление

11.Знать определение простейшей рациональной дроби и уметь представлять правильную рациональную дробь в виде суммы простейших дробей 1

12.Знать определение первообразной и доказывать теорему, что две первообразные одной и той же функции отличаются на постоянную 2

13.Доказывать основные свойства неопределённого интеграла 3

14. Выводить формулы замены переменной и интегрирования по частям для неопределенного интеграла 4

15.Выводить формулы интегрирования простейших рациональных дробей 6

16. Излагать приёмы вычисления интегралов вида: 7

17.Знать определение определенного интеграла. Формулировать теорему существования определенного интеграла. 8

18.Доказывать основные свойства определенного интеграла 10

19. Доказывать теорему о среднем. 11

20.Доказывать теорему о производной определенного интеграла по переменному верхнему пределу и выводить формулу Ньютона–Лейбница 12

21.Выводить формулы замены переменной и интегрирования по частям для определенного интеграла 14

Замена переменной в определённом интеграле 14

22.Выводить формулы, использующие понятие определенного интеграла для его геометрических и механических приложений. 15

27.Знать определение предела и непрерывности функции двух переменных 17

28.Сформулировать свойства функции, непрерывной в замкнутой ограниченной области 19

29.Знать определение частных производных. Уметь выводить формулы производной сложной функции двух переменных, полной производной, производной неявной функции 20

30.Знать определение дифференцируемости функции, доказывать теоремы о необходимом условии дифференцируемости, о достаточном условии дифференцируемости 25

33. Формула касательной к плоскости и нормали 26

34.Необходимые условия экстремума 28

35. Достаточное условие экстремума 29

35. Достаточное условие экстремума (2 вариант) 29

39. Знать определения криволинейных интегралов первого и второго рода и уметь их вычислять 31

41.Знать формулы Грина 33

11.Знать определение простейшей рациональной дроби и уметь представлять правильную рациональную дробь в виде суммы простейших дробей

Всякую рациональную функцию можно представить в виде рациональной дроби, т. е. в виде отношения двух многочленов:

Если степень числителя ниже степени знаменателя, то дробь называется правильной, в противном случае дробь называется неправильной.

Если дробь неправильная, то, разделив числитель на знаменатель (по правилу деления многочленов), можно представить данную дробь в виде суммы многочлена и некоторой правильной дроби:  , где M(x)-многочлен, а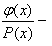  правильная дробь.

Пример: Пусть дана неправильная рациональная дробь.

Тогда  ,так как, при делении уголком получим остаток (4x-6).

Т. к. интегрирование многочленов не представляет принципиальных затруднений, то основная трудность при интегрировании рациональных дробей заключается в интегрировании правильных рациональных дробей.

Можно выделить несколько типов рациональных дробей:

I. Вид:  .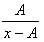

II. Вид: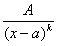   (k-целое положительное число ³2).

III. Вид:  .

IY. Вид:   (k-целое³2).

12.Знать определение первообразной и доказывать теорему, что две первообразные одной и той же функции отличаются на постоянную

Функция F(x) называется первообразной от функции f(x) на отрезке [а,b],если во всех точках этого отрезка выполняется равенство F’(x)=f(x)

Пример: пусть . Тогда первообразная, так как .Функция также первообразная , так как .

Уже из этого примера видно, что у одной функции может быть несколько первообразных. Чем же эти первообразные отличаются друг от друга ?

Теорема .Пусть и две первообразные одной и той же функции .Тогда , где С- постоянная величина (константа).

Доказательство

Действительно, в этом случае и по теореме о постоянстве функции F2(x)-F1(x)=C

Определение 2. Совокупность всех первообразных функции f(x) называется неопределённым интегралом от этой функции и обозначается интеграл f(x)dx.

Функция f(x) называется подинтегральной функцией , а комбинация f(x)dx-подинтегральным выражением.

Пусть F(x) есть какая-то первообразная функции f(x) . Так как две первообразных отличаются только на константу , то

 f(x)dx = F(x)+C

Где С – произвольная константа.

13.Доказывать основные свойства неопределённого интеграла

1. ; –производная неопределенного интеграла равна подынтегральной функции, а его дифференциал–подынтегральному выражению.

Доказательство. Из определения первообразной:

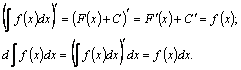
2. – неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого.

Доказательство. Из определения первообразной следует, что функция является первообразной для функции следовательно, является неопределенным интегралом от .

Например,

3. –неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме неопределенных интегралов от этих функций.

Доказательство. Достаточно показать, что совпадают производные левой и правой частей равенства.

–по свойству 1;

.

4. , где k=const–постоянный множитель можно вынести за знак неопределенного интеграла. Доказывается аналогично свойству 3. Из свойств 1 и 2 следует, что дифференцирование и интегрирование являются взаимно обратными действиями.