
- •1. События и их классификация. Классическое определение вероятности
- •2. Элементы комбинаторики: перестановки, сочетания, размещения, правило умножения и правило сложения
- •3. Действия над событиями. Соотношения между событиями
- •4. Теорема сложения вероятностей несовместных событий.
- •5. Теорема сложения вероятностей совместных событий.
- •6. Частота события и ее свойства. Статистическое определение вероятности.
- •7. Условная вероятность. Теорема умножения вероятностей. Вероятность появления хотя бы 1 события
- •8. Формула полной вероятности. Формулы Байеса
- •9. Повторные независимые испытания. Формула Бернулли. Наивероятнейшее число появления события
- •10. Повторные независимые испытания. Формула Пуассона
- •11. Повторные независимые испытания. Локальная и интегральная теорема Лапласа
- •12. Понятие случайной величины и ее функции распределения. Свойства функции распределения
- •13. Дискретные случайные величины. Числовые характеристики (математическое ожидание, дисперсия, среднее квадратическое отклонение, начальные и центральные моменты, асимметрия и эксцесс)
- •14. Биномиальный закон распределения
- •15. Распределение Пуассона
- •16. Непрерывные случайные величины. Плотность распределения. Числовые характеристики (математическое ожидание, дисперсия, среднее квадратическое отклонение)
- •17. Равномерное распределение. Вероятность попадания случайной величины в заданный интервал
- •18. Показательное распределение. Вероятность попадания случайной величины в заданный интервал
- •Характеристики
- •19. Нормальное распределение. Вероятность попадания в заданный интервал нормальной случайной величины. Правило 3-х сигм
- •20. Функции случайных величин
- •21. Понятие системы случайных величин. Закон распределения двумерной случайной величины. Функция распределения двумерной случайной величины
- •22. Понятие о законе больших чисел. Неравенства Маркова и Чебышева
- •23. Теоремы Чебышева и Бернулли. Центральная предельная теорема
- •24. Цепи Маркова. Применение Марковских цепей в экономике
- •25. Выборочный метод. Основные понятия. Полигон и распределения. Эмпирическая функция распределения.
- •26. Оценка параметров по выборке. Понятие несмещённости, состоятельности и эффективности оценки
- •27. Основные характеристики генеральной и выборочной совокупностей
- •28. Связь между характеристиками генеральной и выборочной совокупностей.
- •29. Точечные и интервальные оценки. Доверительная вероятность и доверительный интервал.
- •30. Доверительный интервал для оценки мат.Ожидания нормального распределения
- •31. Понятие корреляционной зависимости. Корреляционная таблица. Линейная корреляция
- •32. Метод наименьших квадратов для определения параметров линейной регрессии
- •33. Статистическая гипотеза. Основные понятия
- •34. Уровень значимости и мощность критерия. Этапы проверки стат.Гипотезы
- •Этапы проверки статистических гипотез
- •35. Проверка гипотезы о значимости выборочного коэффициента корреляции
- •36.Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона
- •37. Основные понятия дисперсионного анализа
22. Понятие о законе больших чисел. Неравенства Маркова и Чебышева
Суть закона больших чисел. Если число случайных величин неограниченно растет, то их среднее арифметическое утрачивает смысл случайной величины и стремится к постоянному числу равному среднему арифметическому их матожиданий.
Для теории вероятности большую роль играют вероятности, которые близки либо к 0, либо к 1. Особую роль при этом играют случайные величины, которые представляют собой сумму большого количества случайных величин.
Последовательность случайных величин 1, 2 и т.д. сходится к по вероятности, если для >0
![]()
Неравенство
Чебышева Вероятность
того, что отклонение случайной величины
X
от ее математического ожидания по
абсолютной величине больше положительного
числа
![]() ,
не больше чем, D(x)/
2.(дисперсия
должна быть ограничена и
,
не больше чем, D(x)/
2.(дисперсия
должна быть ограничена и
![]() )
)
![]() Докажем,
это неравенство для непрерывной случайной
величины с плотностью вероятности P(X)
Докажем,
это неравенство для непрерывной случайной
величины с плотностью вероятности P(X)
![]()
![]()
![]()
![]() Неравенство
Чебышева часто используется для
противоположного события
Неравенство
Чебышева часто используется для
противоположного события
![]()
23. Теоремы Чебышева и Бернулли. Центральная предельная теорема
Если
X1,
X2,…,Xn
– последовательность независимых
случайных величин, имеющих конечные
дисперсии, ограниченные одним и тем же
числом С, то для любого С>0 выполняется
![]()
Доказательство.Введем
в рассмотрение случайную величину –
среднее арифметическое случайных
величин
![]()
Найдем
матожидание
![]()
![]()
И
дисперсию
![]()
Следовательно
– дисперсия конечная. Тогда к
![]() применим неравенство Чебышева
применим неравенство Чебышева
![]()
Переходя
к пределу получим
![]()
А
так как вероятность не может быть больше
1, то предел равен 1.
![]()
Следствием теоремы Чебышева является теорема Бернулли.
Пусть
![]() -
число появления события А в n
испытаниях в схеме Бернулли, и p
– вероятность появления А в одном
испытании. Тогда для любого
справедливо
-
число появления события А в n
испытаниях в схеме Бернулли, и p
– вероятность появления А в одном
испытании. Тогда для любого
справедливо
![]()
![]() -частота
появления события.
-частота
появления события.
Пусть
![]() ,
где
,
где
![]() - число появления события А в i-ом
испытании.
- число появления события А в i-ом
испытании.
Дисперсия любой величины равна произведению pq, так как p+q=1, то p*q не превышает ¼, и следовательно дисперсии всех величин ограничены числом c=1/4
Применим
теорему Чебышева
![]()
так как матожидание равно вероятности наступления события.
Так
как
![]() равна относительной частоте появления
события А (m/n)(каждая
величина
1,
2,
n
при появлении события в соответствующем
испытании равна 1 и поэтому их суму равна
m),
то окончательно получим
.
равна относительной частоте появления
события А (m/n)(каждая
величина
1,
2,
n
при появлении события в соответствующем
испытании равна 1 и поэтому их суму равна
m),
то окончательно получим
.
Пусть
![]() - последовательность независимых
случайных величин. Обозначим через
- последовательность независимых
случайных величин. Обозначим через
![]() их сумму.
их сумму.
Говорят,
что к последовательности
![]() применима
центральная предельная теорема, если
применима
центральная предельная теорема, если
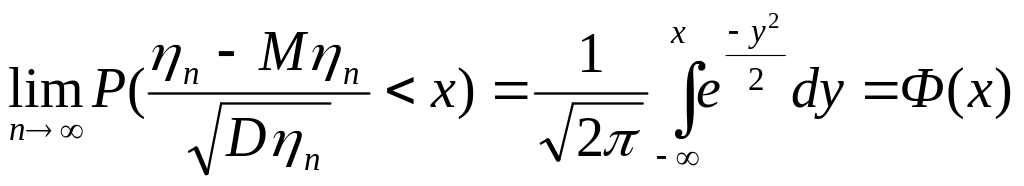
По
определению F(x)=P(![]()
![]()
Суть ЦТП Если число случайных величин неограниченно растет, то их сумма стремится к нормальному распределению независимо от того как распределены слагаемые.
В природе все имеет нормальное распределение.
Частным
случаем ЦПТ является интегральная
теорема Муавра-Лапласса. Если в ней
подставить
![]() ,
а вместо b=x,
то
,
а вместо b=x,
то
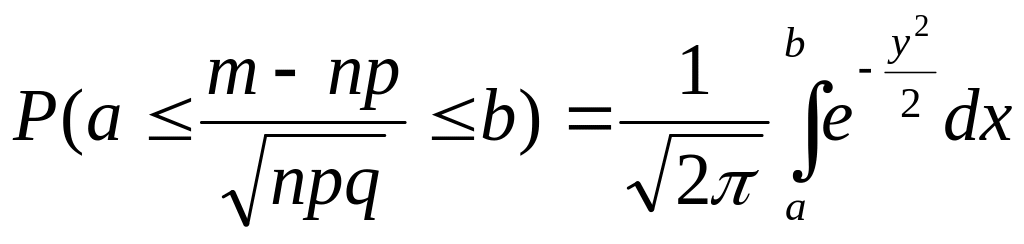
24. Цепи Маркова. Применение Марковских цепей в экономике
Теорема.
Если
сл\в Х примет только неотриц знач и имеет
мат\ожидание, то для любого положительного
числа А верно неравенство:
![]() .
Доказательство
для дискретной сл\в Х: Расположим
значения дискр сл\в Х в порядке возрастания,
из кот часть значений
.
Доказательство
для дискретной сл\в Х: Расположим
значения дискр сл\в Х в порядке возрастания,
из кот часть значений
![]() будет не больше числаА, а др часть
будет не больше числаА, а др часть
![]() будут
больше А, т.е
будут
больше А, т.е
![]()
Запишем
выражение для м\о
M(X):
![]() ,
где
,
где
![]()
-
вер-ти т\ч сл\в Х примет значения
![]() .
Отбрасывая первые k
неотрицательных слагаемых получим:
.
Отбрасывая первые k
неотрицательных слагаемых получим:
![]() .
Заменяя в этом неравенстве значения
меньшим числом, получим неравенство:
.
Заменяя в этом неравенстве значения
меньшим числом, получим неравенство:
![]() или
или
![]() .
Сумма вер-тей в левой части представляет
сумму вер-ей событий
.
Сумма вер-тей в левой части представляет
сумму вер-ей событий
![]() ,
т.е вер-ть соб Х>А. Поэтому
,
т.е вер-ть соб Х>А. Поэтому
![]() .
Т.к события
.
Т.к события
![]() и
и
![]() противоположные,
то заменяя
противоположные,
то заменяя
![]() выражением
выражением
![]() ,
придём к др форме неравенства Маркова:
,
придём к др форме неравенства Маркова:
![]() .
Неравенство
Маркова применимо к любым неотрицательным
сл\в.
.
Неравенство
Маркова применимо к любым неотрицательным
сл\в.
