30. Доверительный интервал для оценки мат.Ожидания нормального распределения

Пусть CВ Х распределена нормально т. е. ген. с-ть – нормально распределенная CВ с переменными: и . Для нормальной СВ Х с переменными  и  имеет место ф-ла вер-ти отклонения нормальной СВ: .

В нашем случае: , =>0, (х)= , СВ Х= . Тогда получаем . Зададим доверительную вероятность , тогда . Это вероятность того, что выборочная характеристика отличается от ген средней по абсолютной величине меньше чем на , тогда имеем: → t_y= . Рассмотрим = - точность оценки (предельная ошибка выборки). Получим интервал: на этом интервале с надежностью(доверит вероятностью)  находится неизвестная вероятная средняя Примечание: если ₀ неизвестна, ее заменяют приближенно исправленной стат дисперсией S

(Если отбор бесповторный, то мера точности  имеет вид: = )

31. Понятие корреляционной зависимости. Корреляционная таблица. Линейная корреляция

Если изменение одной из случайных величин влечет изменение среднего другой случайной величины, то стат.зависимость называют корреляционной. Сами случайные величины, связанные коррреляционной зависимостью, оказываются коррелированными.

Корреляционную зависимость Y от X можно описать с помощью уравнения вида: yx=f(x) (1)

где y_x - условное среднее величины Y, соответствующее значению x величины X, а f(x) некоторая функция. Уравнение (1) называется выборочным уравнением регрессии Y на X. Функцию f(x) называют выборочной регрессией Y на X, а ее график – выборочной линией регрессии Y на X.

Совершенно аналогично выборочным уравнением регрессии X на Y является уравнение: x_y=φ(y)

Пусть величина Х в выборке принимает значения x₁, x₂,....x_m, где количество различающихся между собой значений этой величины, причем в общем случае каждое из них в выборке может повторяться. Пусть величина Y в выборке принимает значения y₁, y₂,....y_k, где k - количество различающихся между собой значений этой величины, причем в общем случае каждое из них в выборке также может повторяться. В этом случае данные заносят в таблицу с учетом частот встречаемости. Такую табл. с группированными данными называют корреляц-ой.

Если две случайные величины Х и Y имеют в отношении друг друга линейные функции регрессии, то говорят, что величины Х и Y связаны линейной корреляционной зависимостью.

32. Метод наименьших квадратов для определения параметров линейной регрессии

Выбрав вид функции регрессии, т.е. вид рассматриваемой модели зависимости Y от Х (или Х от У), напр/, линейную модель y_x=a+bx, необходимо определить конкретные значения коэффиц. модели.

При различных значениях а и b можно построить бесконечное число зависимостей вида y_x=a+bx т.е на координатной плоскости имеется бесконечное количество прямых, нам же необходима такая зависимость, которая соответствует наблюдаемым значениям наилучшим образом. Таким образом, задача сводится к подбору наилучших коэффициентов. Линейную функцию a+bx ищем, исходя лишь из некоторого количества имеющихся наблюдений. Для нахождения функции с наилучшим соответствием наблюдаемым значениям используем метод наименьших квадратов.

Обозначим: Y_i - значение, вычисленное по уравнению Y_i=a+bx_i. y_i - измеренное значение, ε_i=y_i-Y_i - разность между измеренными и вычисленными по уравнению значениям, ε_i=y_i-a-bx_i.

В методе наименьших квадратов требуется, чтобы ε_i, разность между измеренными y_i и вычисленными по уравнению значениям Y_i, была минимальной. Следовательно, находим коэффициенты а и b так, чтобы сумма квадратов отклонений наблюдаемых значений от значений на прямой линии регрессии оказалась наименьшей:

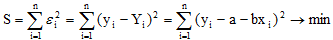
Исследуя на экстремум эту функцию аргументов а и с помощью производных, можно доказать, что функция принимает минимальное значение, если коэффициенты а и b являются решениями системы:

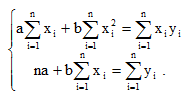
Если разделить обе части нормальных уравнений на n, то получим:

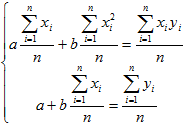
Учитывая, что

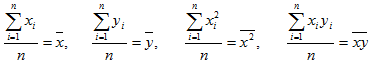
Получим 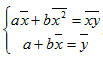, отсюда , подставляя значение a в первое уравнение, получим:

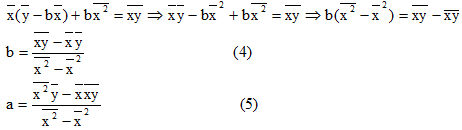
При этом b называют коэффициентом регрессии; a называют свободным членом уравнения регрессии и вычисляют по формуле:

Полученная прямая является оценкой для теоретической линии регрессии. Имеем: