16. Непрерывные случайные величины. Плотность распределения. Числовые характеристики (математическое ожидание, дисперсия, среднее квадратическое отклонение)

Случайная величина называется непрерывной, если для нее существует неотрицательная кусочно-непрерывная функция , удовлетворяющая для любых значений x равенству

   Функция называется плотностью распределения вероятностей, или кратко, плотностью распределения. Если x₁<x₂, то

   Исходя из геометрического смысла интеграла как площади, можно сказать, что вероятность выполнения неравенств равна площади криволинейной трапеции с основанием [x₁,x₂], ограниченной сверху кривой .

 Математическим ожиданием непрерывной случайной величины с плотностью распределения называется число, определяемое равенством

Дисперсия непрерывной случайной величины  определяется равенством

Дисперсия непрерывной случайной величины имеет те же свойства, что и дисперсия дискретной случайной величины. Величина называется среднеквадратическим отклонением.

17. Равномерное распределение. Вероятность попадания случайной величины в заданный интервал

Закон равномерного распределения вероятностей непрерывной случайной величины используется при имитационном моделировании сложных систем на ЭВМ как первоначальная основа для получения всех необходимых статистических моделей. При этом, если специально не оговорен закон распределения случайных чисел, то имеют ввиду равномерное распределение. Распределение вероятностей называют равномерным, если на интервале (a,b), которому принадлежат все возможные значения случайной величины, дифференциальная функция распределения имеет постоянное значение, т. е. f(x) = C. Так как то Отсюда закон равномерного распределения аналитически можно записать так: График дифференциальной функции равномерного распределения вероятностей Интегральную функцию равномерного распределения аналитически можно записать так:

График интегральной функции равномерного распределения вероятностей

18. Показательное распределение. Вероятность попадания случайной величины в заданный интервал

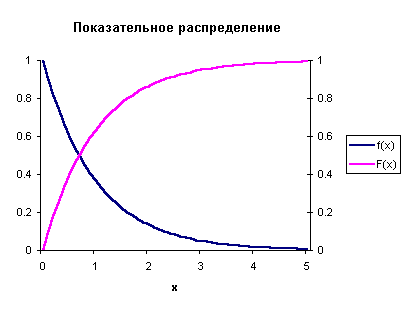
Говорят, что случайная величина X имеет показательное (экспоненциальное) распределение с параметром λ > 0, если она непрерывна, принимает только положительные значения, и имеет плотность распределения f(x) = λe^-λx при 0 < x < ∞.

На следующем рисунке показаны графики плотности (привязан к левой вертикальной оси ординат) и функции (привязан к правой оси ординат) показательного распределения с параметром λ = 1.

Характеристики

Плотность распределения	f(x) = λe-λx
Функция распределения	F(x) = 1 - e-λx
Математическое ожидание	1 / λ
Стандартное отклонение	1 / λ
Дисперсия	1 / λ2
Асимметрия	2
Островершинность	6
Медиана	ln(2) / λ
Мода	0