
- •1. События и их классификация. Классическое определение вероятности
- •2. Элементы комбинаторики: перестановки, сочетания, размещения, правило умножения и правило сложения
- •3. Действия над событиями. Соотношения между событиями
- •4. Теорема сложения вероятностей несовместных событий.
- •5. Теорема сложения вероятностей совместных событий.
- •6. Частота события и ее свойства. Статистическое определение вероятности.
- •7. Условная вероятность. Теорема умножения вероятностей. Вероятность появления хотя бы 1 события
- •8. Формула полной вероятности. Формулы Байеса
- •9. Повторные независимые испытания. Формула Бернулли. Наивероятнейшее число появления события
- •10. Повторные независимые испытания. Формула Пуассона
- •11. Повторные независимые испытания. Локальная и интегральная теорема Лапласа
- •12. Понятие случайной величины и ее функции распределения. Свойства функции распределения
- •13. Дискретные случайные величины. Числовые характеристики (математическое ожидание, дисперсия, среднее квадратическое отклонение, начальные и центральные моменты, асимметрия и эксцесс)
- •14. Биномиальный закон распределения
- •15. Распределение Пуассона
- •16. Непрерывные случайные величины. Плотность распределения. Числовые характеристики (математическое ожидание, дисперсия, среднее квадратическое отклонение)
- •17. Равномерное распределение. Вероятность попадания случайной величины в заданный интервал
- •18. Показательное распределение. Вероятность попадания случайной величины в заданный интервал
- •Характеристики
- •19. Нормальное распределение. Вероятность попадания в заданный интервал нормальной случайной величины. Правило 3-х сигм
- •20. Функции случайных величин
- •21. Понятие системы случайных величин. Закон распределения двумерной случайной величины. Функция распределения двумерной случайной величины
- •22. Понятие о законе больших чисел. Неравенства Маркова и Чебышева
- •23. Теоремы Чебышева и Бернулли. Центральная предельная теорема
- •24. Цепи Маркова. Применение Марковских цепей в экономике
- •25. Выборочный метод. Основные понятия. Полигон и распределения. Эмпирическая функция распределения.
- •26. Оценка параметров по выборке. Понятие несмещённости, состоятельности и эффективности оценки
- •27. Основные характеристики генеральной и выборочной совокупностей
- •28. Связь между характеристиками генеральной и выборочной совокупностей.
- •29. Точечные и интервальные оценки. Доверительная вероятность и доверительный интервал.
- •30. Доверительный интервал для оценки мат.Ожидания нормального распределения
- •31. Понятие корреляционной зависимости. Корреляционная таблица. Линейная корреляция
- •32. Метод наименьших квадратов для определения параметров линейной регрессии
- •33. Статистическая гипотеза. Основные понятия
- •34. Уровень значимости и мощность критерия. Этапы проверки стат.Гипотезы
- •Этапы проверки статистических гипотез
- •35. Проверка гипотезы о значимости выборочного коэффициента корреляции
- •36.Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона
- •37. Основные понятия дисперсионного анализа
7. Условная вероятность. Теорема умножения вероятностей. Вероятность появления хотя бы 1 события
Часто интересует вероятность появления события А, после того, как некоторое событие В произошло. Такую вероятность называют условной и обозначают P(A/B).
Опред 1 Условной вероятностью события А при условии, что событие В уже произошло называется
P(A/B)=![]() ,
P(B)>0
,
P(B)>0
Аналогично, условной вероятностью события B при условии, что событие A уже произошло называется
P(B/A)=![]() ,
P(A)>0
,
P(A)>0
Из
формул следует теорема
умножения:P(AB)=
![]() =
=![]()
Вероятность произведения двух произвольных событий равна произведению вероятности одного из событий на условную вероятность второго, при условии, что первое уже произошло.
Распространим теорему умножения на конечное число событий
P(A1A2Ak)=P(A1)P(A2/A1)*…*P(Ak/A1A2 ,,,Ak-1)
Опред 2 События А и В называются независимыми, если вероятность произведения равна произведению вероятности этих событий.
P(AB)=P(A)P(B)
Для независимых событий условные и безусловные вероятности совпадают. P(A/B)=P(A)
Для конечного числа независимых событий вероятность произведения равна произведению вероятностей. P(A1A2…Ak)=P(A1)P(A2)…P(AK)
Теорема. Вероятность появления хотя бы одного из событий А1 , А2 , ..., Аn , независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
Р (A) = 1 — q1q2 ... qn.
Доказательство
Ч а с т н ы й с л у ч а й. Если события А1 , А2 , ..., Аn имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий
P (A) = l — qn.
8. Формула полной вероятности. Формулы Байеса
Пусть событие А может произойти только с одним из n несовместных событий H1…Hn, образующих полную группу, т.е. Нi * Нj= Ø, i j, Н1+… +Нn=Ω.
События А*Hi и A*Hj являются несовместными.
Применяя теорему умножения к каждому слагаемому получим формулу полной вероятности.
![]()
События H1, H2,…, Hn часто называют гипотезами.
Иногда
интересует как перераспределяется
вероятность гипотез, после того как
событие А произошло
![]()
По
теореме умножения вероятность произведения
этих двух событий равна![]()
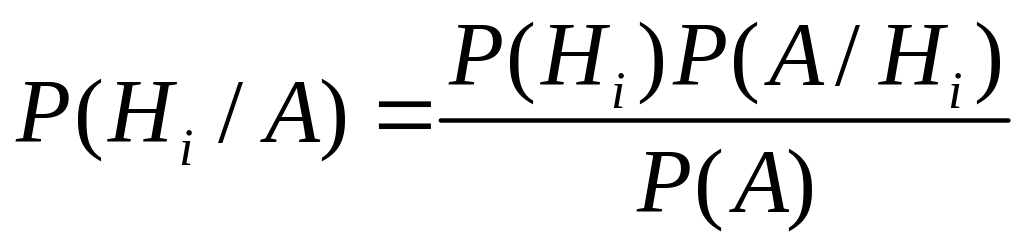
Подставляя в знаменатель формулу полной вероятности получим формулу Байеса:
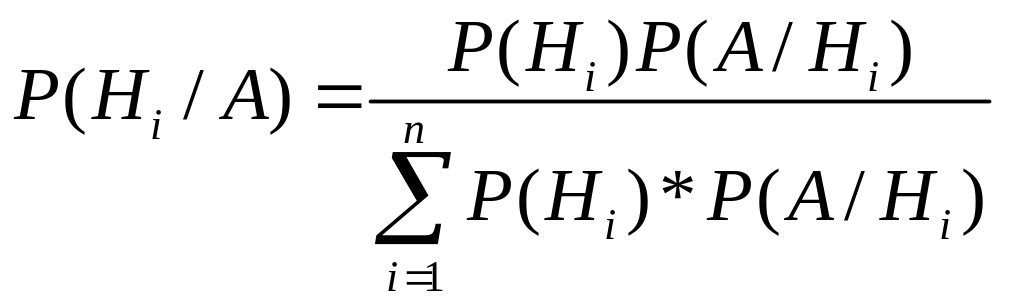
9. Повторные независимые испытания. Формула Бернулли. Наивероятнейшее число появления события
Пусть производится последовательность независимых испытаний, в каждом из которых возможно только 2 исхода. Событие А или появится или не появится. Обозначим вероятность появления события А – p, не появления – q.
Под элементарным событием в схеме Бернулли принимается последовательность наступления или ненаступления события А в n испытаниях
А={1},
![]() ={0}.
Тогда элементарный исход имеет вид
(1,0,…, 1)
={0}.
Тогда элементарный исход имеет вид
(1,0,…, 1)
Найдем вероятность того, что в n испытаниях событие появится ровно m раз.
Для
произвольных m
и n
вероятность одного элементарного исхода
равна pmqn-m
.
Число таких элементарных исходов равно
числу способов разместить m
единиц по n
местам, а это по определению число
сочетаний m
элементов по n.
Получим формулу Бернулли
![]()
Часто
интересует появление события А не ровно
m
раз, а от k1
до k2.

