29. Точечные и интервальные оценки. Доверительная вероятность и доверительный интервал.

Пусть вид распределения изучаемого признака X известен, но неизвестны значения входящего параметра σ. Например, пусть X имеет нормальное распределение и нужно оценить значение параметров.

Статистическая оценка – любая функция выборки.

σ =f(x₁,x₂,…,x_n) σ - стат. оценка.

Точечной оценкой называется оценка, которая дается одним числом.

Для того, чтобы стат. Оценка давала значение приближенное к σ, она должна обладать определенными свойствами.

1. оценка σ называется несмещенной, если ее матожидание = оцениваемому параметру M(σ)=θ.

Это свойство означает отсутствие ошибки одного знака.

Примерами несмещенных оценок являются любые начальные эмпирические моменты для соответствующих теоретических. Покажем это для начальных моментов первого порядка, т.е. покажем, что несмещенной оценкой МО является выборочная средняя. , σ - оценка МО.

Выборочное значение x₁, x₂,…,x_n рассматривается как случайная величина, имеющая одно и то же распределение, тогда обозначим M(x_i )=a, D(x_i )=

M(

Примером смещенной оценки является выборочная дисперсия для теоретической дисперсии

Для того, чтобы получить несмещенную оценку вводится понятие исправленной выборочной дисперсии.

Оценка σ называется состоятельной, если при она стремится по вероятности к оцениваемому параметру.

На основании закона больших чисел можно показать, что среднее значение является состоятельной оценкой для МО

Можно показать, что начальный и центральный эмпирические моменты являются состоятельными оценками соответствующих теоретических моментов.

В частности выборочная дисперсия является состоятельной оценкой теоретической.

При больших объемах выборки нет необходимости вычислять s². Вычислять его надо, если n<30.

Оценка σ называется эффективной, если она имеет наименьшую возможную дисперсию среди всех других оценок, вычисленных по выборке объема n.

Оценка неизвестного параметра, который задается двумя числами (концами интервала) называется интервальной.

Пусть по выборке получена точечная оценка σ неизвестного параметра . Это оценка чем точнее, чем меньше | - σ |.

Пусть | - σ |< , >0.

Методы математической статистики не позволяют на 100% утверждать, что выполняется это неравенство.

P(| - σ |< )= -доверительная вероятность или надежность. выбирается исследователем самостоятельно.

P( - < < + )=

Доверительным называется интервал ( - ; + ), который покрывает неизвестный параметр с заданной надежностью .

- точность оценки.

Замечание: Неверно говорить, что попадает в интервал. Задача состоит в том, чтобы построить такой интервал, который бы заключал в себе .

Доверительные интервалы строятся следующим образом: 1. вычисляется точечная оценка 2. выбирается надежность 3. вычисляется точность оценки

Пусть изучаемый признак Х имеет нормальное распределение и значение параметра известно. Построим по выборке (x₁, x₂,…,x_n) доверительный интервал для оценки а.

Несмещенной и состоятельной оценкой матожидания является выборочная средняя.

Пусть выбрали, найдем

~(пропорционально, или зависит от) N(a, )

Можно показать, что линейная комбинация нормальной случайной величины также имеет нормальное распределение.

M( D(

, т.е.

Чтобы воспользоваться стандартными формулами сделаем для преобразование стандартизации.

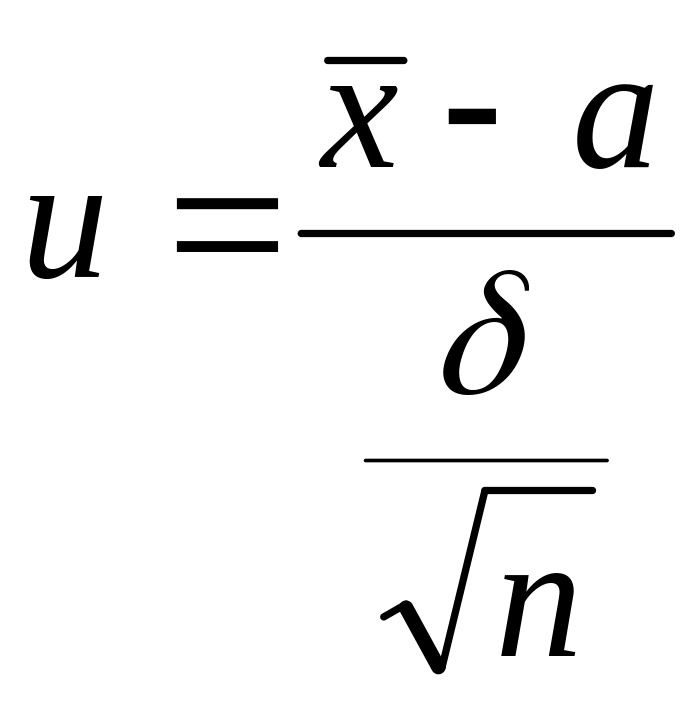
Оценим вероятность P(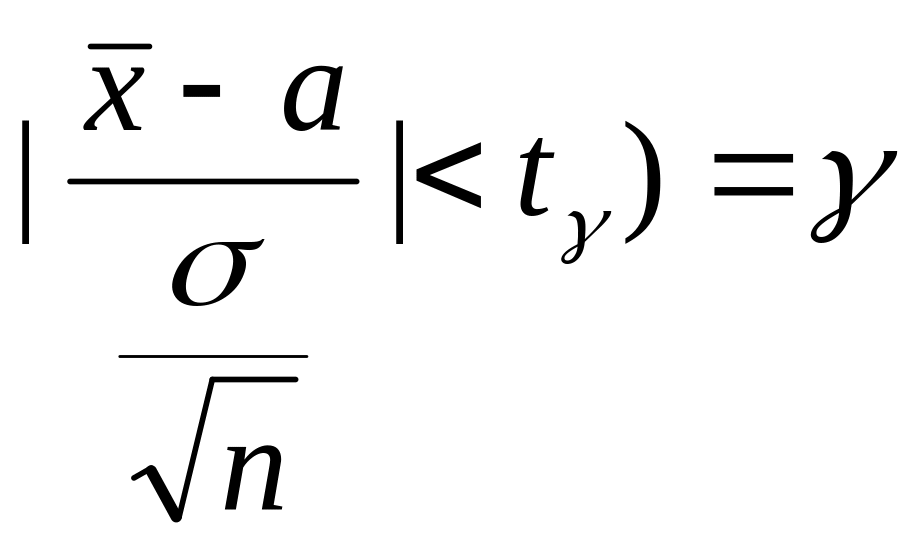

Воспользуемся формулой вероятности заданного отклонения для нормальной случайной величины.

P(

= =

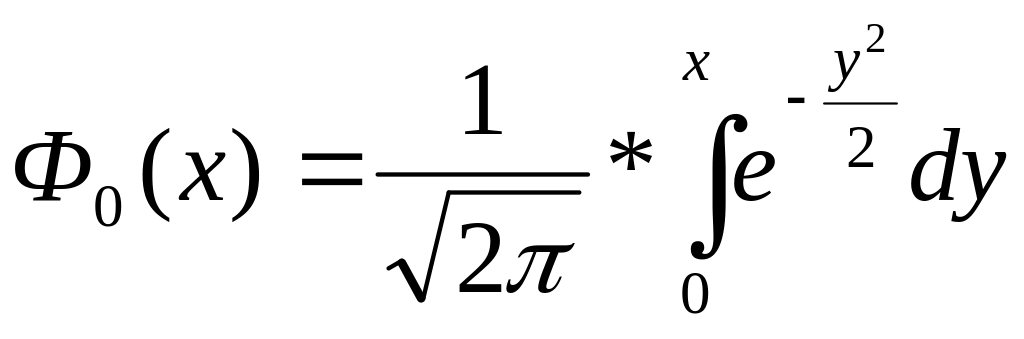
Тогда доверительные интервалы будет иметь вид

Замечание. Пусть требуется определить объем выборки, которая обеспечивает заданную надежность и точность n=

Если n дробное, то его всегда следует округлить до ближайшего целого с избытком