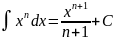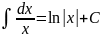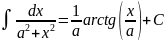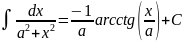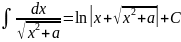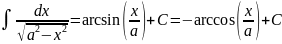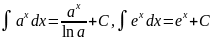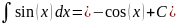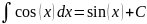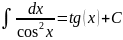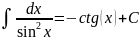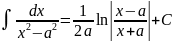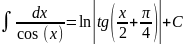Направление выпуклости. Точки перегиба.
График функции имеет выпуклость вверх (вниз) на интервале, если на этом интервале график расположен не выше (не ниже) касательной к графику функции, проведенной в любой точке этого интервала.
Необходимое условие выпуклости вверх (вниз). Если функция у=f(x) в каждой точке интервала (a,b) имеет f’’(x)≤0 (f’’(x)≥0), то график функции на этом интервале имеет выпуклость вверх (вниз).
Необходимое условие точки перегиба. Если в точке график функции имеет точку перегиба, а сама функция имеет вторую производную в окрестности этой точки, то такая производная обращается в ноль.
Достаточное условие точки перегиба. Если функция имеет вторую производную в окрестности точки, и в самоц точке эта производная обращается в ноль, тогда если в указанной окрестности вторая производная имеет разные знаки слева и справа от данной точки, то в этой точке функция имеет перегиб.
Асимптоты.
Прямая L называется асимптотой графика у=f(x), если расстояние от точки M (x,y), лежащей на кривой стремится к нулю при неограниченном удалении этой точки от начала координат (т.е. при стремлении хотя бы одной из координат точки к бесконечности).
Существуют вертикальные, горизонтальные и наклонные асимптоты.
Если
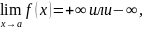 то прямая х=а является вертикальной
асимптотой.
то прямая х=а является вертикальной
асимптотой.
Если
 то
прямая y=b
является горизонтальной асимптотой.
то
прямая y=b
является горизонтальной асимптотой.
Прямая
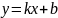 является наклонной асимптотой графика
функции
является наклонной асимптотой графика
функции
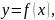 если одновременно существуют пределы:
если одновременно существуют пределы:

Или
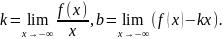
Понятие дифференциал.
Полным приращением функции является:

Дифференциалом
dy
называется главная, линейно относительно
∆x,
часть полного приращения функции.
Следовательно, дифференциал
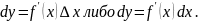
Первообразная функции. Неопределенный интеграл и его свойства.
Функция F(x) называется первообразной по отношению к функции f(x), если функция F(x) дифференцируема и выполняется условие F’(x)=f(x).
Неопределенным интегралом от функции f(x) называется множество всех её первообразных. Неопределенный интеграл обозначается
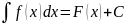
Свойства неопределенного интеграла:
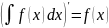
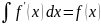
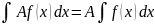
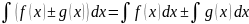
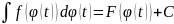
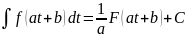 .
.
Таблица интегралов.
Таблица простейших интегралов имеет следующий вид (без дифференциалов).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Основные методы интегрирования.
Существует несколько основных методов интегрирования.
В отдельных случаях можно использовать метод интегрирования по частям:
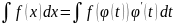
Так же можно использовать формулу интегрирования по частям:
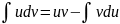
При помощи этих методов некоторые интегралы удается привести к табличному виду и найти их значение.
Рациональные дроби. Простейшие рациональные дроби и их интегрирование.
Выражения
типа
 ,
где
,
где
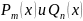 – многочлены n-ой
и m-ой
степени называются рациональной дробью.
Рациональная дробь называется правильной,
если m<n
и неправильной, если m≥n.
Если дробь неправильная, необходимо
путем деления выделить целую часть.
Затем, знаменатель правильной дроби
необходимо разложить на множители,
разделить дробь на несколько дробей, в
знаменателях которых находятся множители
и путем несложных математических
преобразований получить несколько
табличных интегралов.
– многочлены n-ой
и m-ой
степени называются рациональной дробью.
Рациональная дробь называется правильной,
если m<n
и неправильной, если m≥n.
Если дробь неправильная, необходимо
путем деления выделить целую часть.
Затем, знаменатель правильной дроби
необходимо разложить на множители,
разделить дробь на несколько дробей, в
знаменателях которых находятся множители
и путем несложных математических
преобразований получить несколько
табличных интегралов.
Интегрирование рациональных дробей.
См предыдущий вопрос.
Интегрирование простейших иррациональных функций.
Интеграл вида
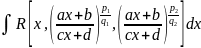
Где
R
– рациональная функция, а
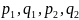 –
целые числа находят при помощи подстановки
–
целые числа находят при помощи подстановки
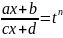 ,
где n
– наименьшее общее кратное
,
где n
– наименьшее общее кратное
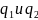 .
.