11.6. Построение гарантированных от риска комбинационных схем

В этом разделе, рассматривается реализация функции

в двух вариантах: а) при помощи элементов И-НЕ и б) при помощи элементов ИЛИ-НЕ. Предположим, что схемы строятся из элементов с максимальным числом входов, равным 3.

П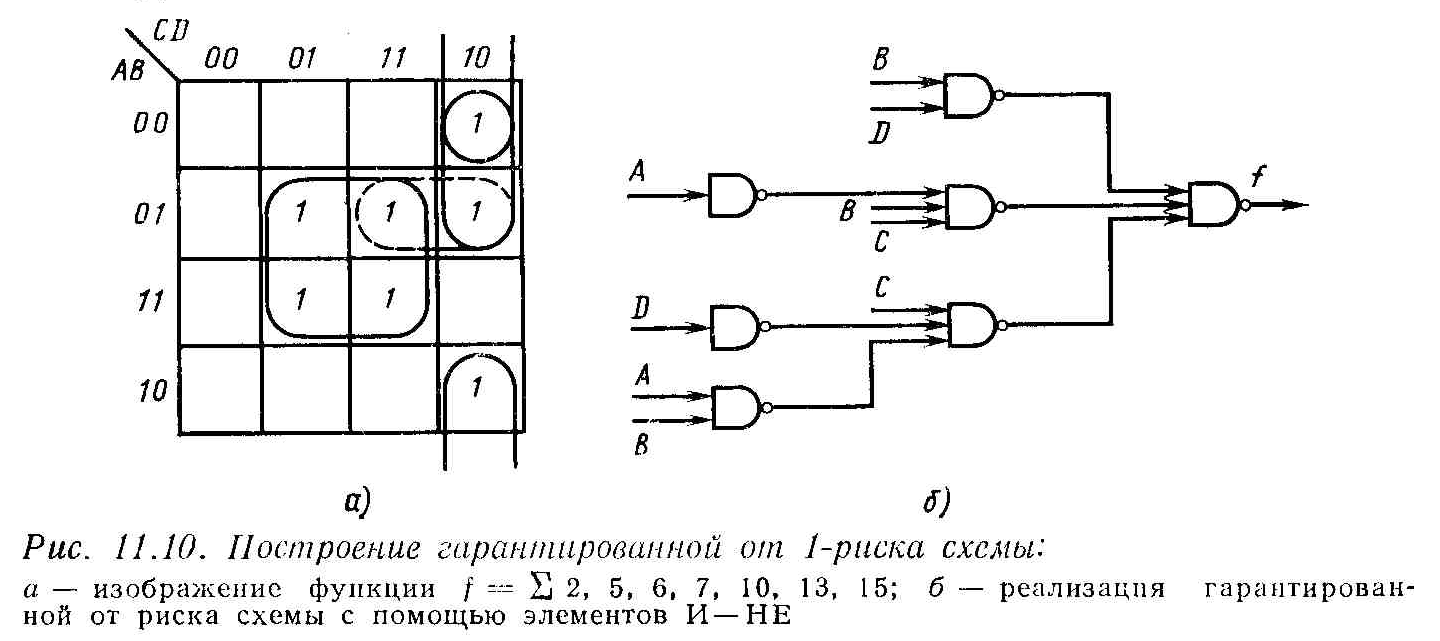 оскольку в первом варианте реализации схемы используются элементы И-НЕ, необходимо получить функцию, гарантированную от статического 1-риска. Сначала следует отразить на карте Карно все те комбинации переменных, при которых функция равна логической «1», как показано на рис. 11.10, а, и упростить их обычным способом. Далее необходимо проверить, нет ли единиц в смежных ячейках, не покрытых одной и той же первичной импликантой. В рассматриваемом случае такими ячейками являются 0111 и 0110 и для устранения непокрытых смежных ячеек добавлена дополнительная первичная импликанта. Единицы, соответствующие дополнительной первичной импликанте, обведены на карте Карно штриховой линией.

Полученная на карте гарантированная от риска функция может быть записана в виде

.

Чтобы удовлетворить условию ограниченности числа входов, это выражение может быть факторизовано, после чего оно примет следующий вид:

.

В результате такой факторизации ситуации риска повторно не возникают. В рассматриваемой задаче риск должен был бы появляться при А = 0, В = 1 и С = 1, а также при изменении D от 1 до 0. При этих условиях факторизованное выражение примет вид

,

т. е. функция удовлетворяет условию устранения риска.

Реализация гарантированной от риска функции с помощью элементов И-НЕ показана на рис. 11.10, б.

Для того чтобы получить гарантированную от риска реализацию данной функции на элементах ИЛИ-НЕ, сначала необходимо изобразить на карте Карно все те комбинации переменных, при которых значение функции равно логическому «0», а затем упростить ее обычным способом. Определенная на нулевых

з 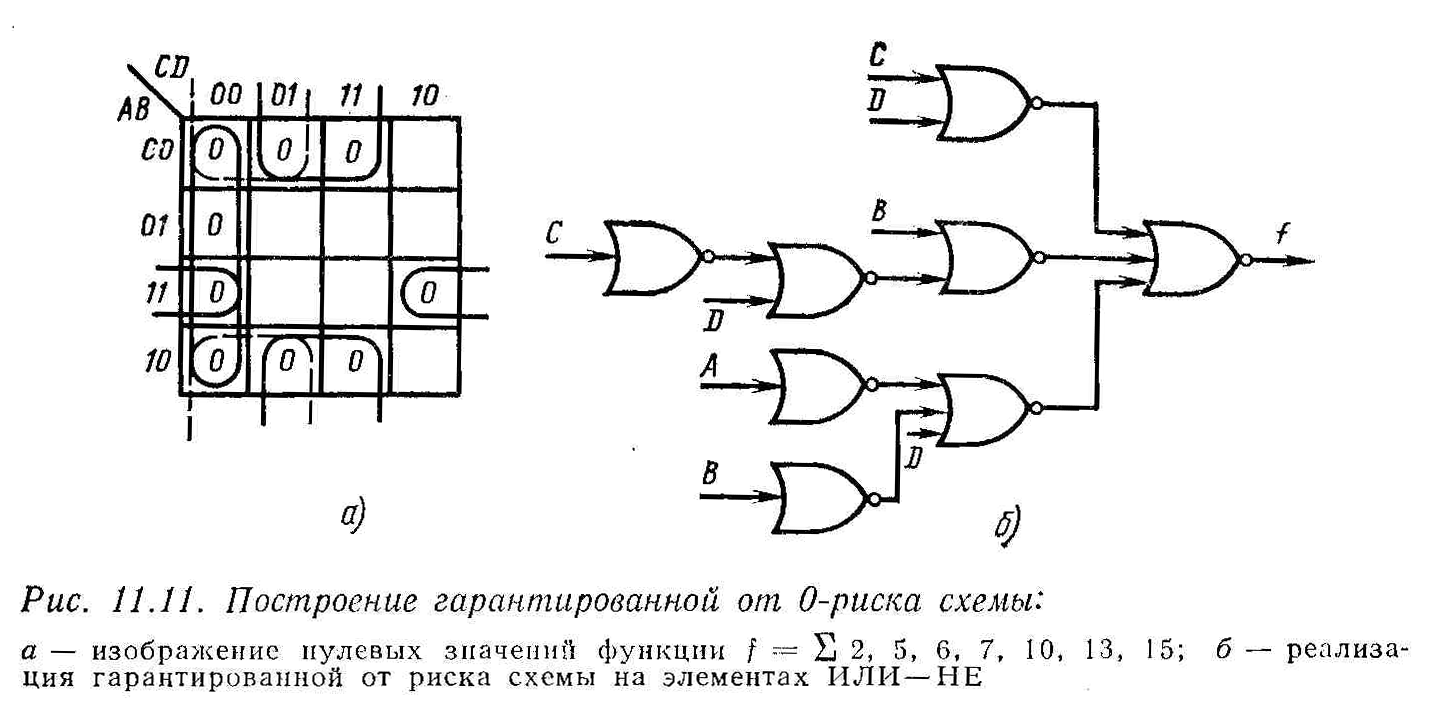начениях функция представляет собой инверсию рассматриваемой функции, и карта Карно с ее изображением получается из карты на рис. 11.10, а при помощи заполнения ее свободных ячеек нулями, как показано на рис. 11.11, а.

Наличие, нулей в смежных ячейках, не покрытых одной и той же первичной импликантой, показывает, что упрощенная функция имеет статический 0-риск, обусловливаемый некоторыми определенными ранее условиями. В этом примере такими смежными ячейками являются: а) 0000 и 0001; б) 1000 и 1001. Присоединение дополнительной первичной импликанты ВС позволяет покрыть эти смежные ячейки и удалить 0-риск. Нули, соответствующие дополнительной первичной импликанты, обведены штриховыми линиями на рис. 11.11, а. Полученная на карте инверсная функция имеет вид

.

В результате факторизации, выполняемой для удовлетворения ограничения на число входов у одного элемента, получаем следующую функцию:

.

Найдем двойственную к ней функцию

и затем ее инверсию

.

Реализация этой гарантированной от риска функции с помощью элементов ИЛИ-НЕ показана на рис. 11.11, б.

11.7. Анализ схем для обнаружения ситуаций риска

На рис. 11.12, а изображена схема на элементах ИЛИ/И, которую следует проверять на наличие какого-либо риска. Так как схема состоит из элементов ИЛИ и И одновременно, в ней может возникать ситуация статического риска как в нуле, так и в единице. Функция для этой схемы имеет вид

,

и она может быть развернута следующим образом:

.

Э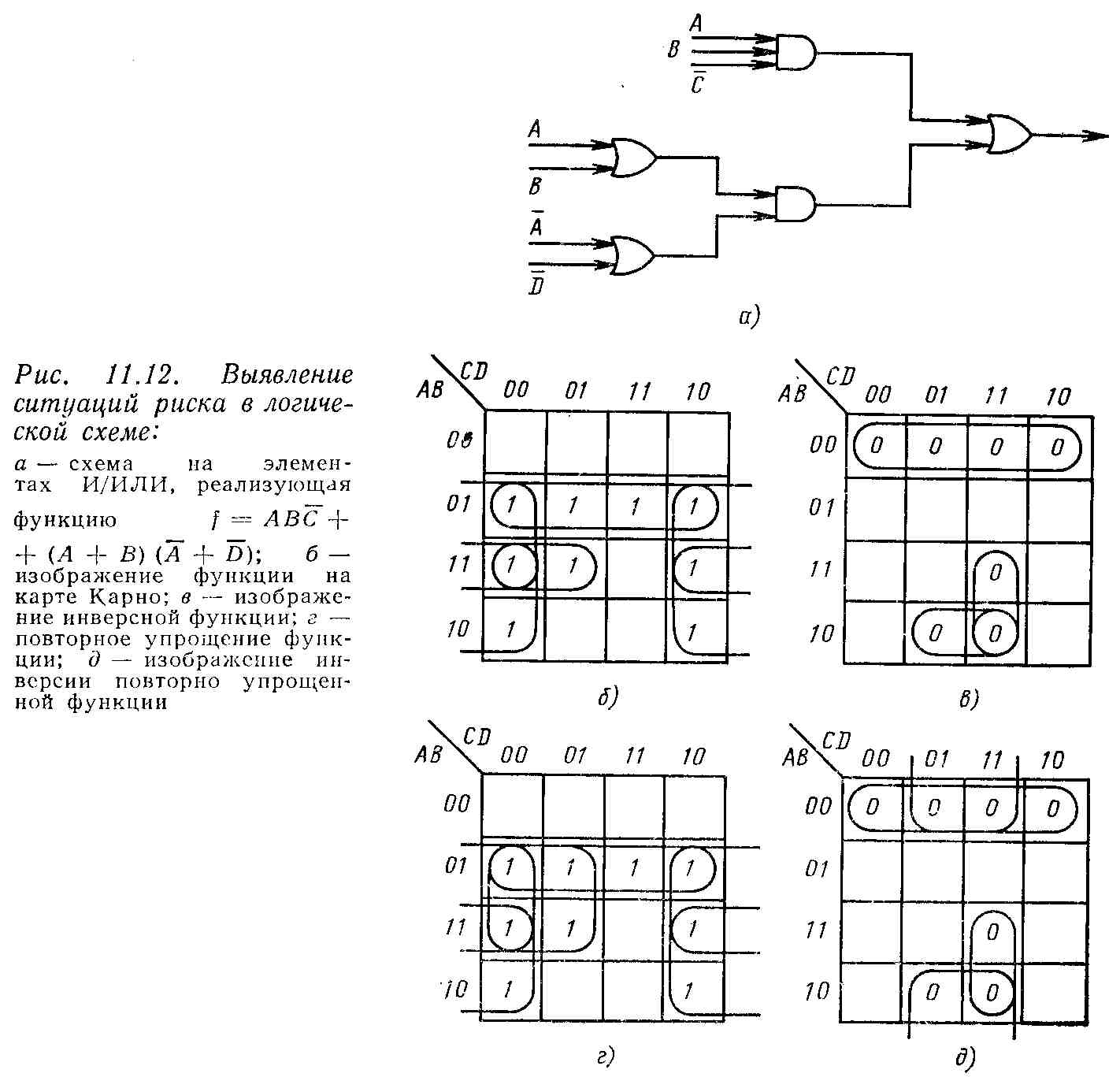 то выражение содержит терм , который при обычных обстоятельствах был бы устранен, так как по законам алгебры логики он равен логическому 0. Однако, поскольку А и в комбинационных схемах могут быть одновременно равны логической «1», они считаются независимыми переменными в приведенном выражении, полная форма которого необходима для демонстрации переходных процессов.

Для того чтобы обнаружить ситуации риска, необходимо при определенных входных условиях рассмотреть, к какой форме сводится развернутое выражение (к или ). Например, если B=0, C = 0 u D = 1,то выражение приводится к . Следовательно, для этих входных условий при изменении А из 0 в 1 появляется статический 0-риск.

При определении временного уравнения схемы некоторыми теоремами алгебры логики нельзя пользоваться. Для преобразования временного уравнения схемы не могут быть применены те правила, в которых используются тождества и . Например, нельзя пользоваться теоремой алгебры логики, согласно которой , поскольку в ней с помощью тождества выражение приводится к форме . Выше в этой главе было показано, что А и могут быть одновременно равны нулю, и в этом случае . Тогда приведенная выше теорема не является справедливой для всех моментов времени.

Если В = 1, С = 0 и D = 1, выражение преобразуется к виду .В этом случае при изменении А от 1 до 0 появляется ситуация статического 1-риска. Следует отметить, что при изменении А от 1 до 0 значение терма и оно может стать равным 1, только когда А изменяется из 0 в 1.

Если В = 1, С = 0 и D = 0, равенство преобразуется к виду . В этом случае f = 1 независимо от значений А и , следовательно, ситуация статического риска не возникает.

Другим способом статический 1-риск может быть обнаружен определением на картах Карно тех комбинаций переменных, при которых значение функции f = 1, как показано на рис. 11.12, б. Анализируя эту карту, можно заметить, что две смежные ячейки 1101 и 0101, отмеченные «1», не покрыты одной и той же первичной импликантой. Включение дополнительной первичной импликанты обеспечит покрытие этих двух ячеек одной и той же первичной импликантой и устранит статический 1-риск.

Для обнаружения статического 0-риска функция должна быть сначала инвертирована и изображена на карте Карно. Рассматриваемая здесь функция имеет вид

.

Определим двойственную к ней функцию

,

затем функцию, инверсную к ней:

и, наконец, используя теорему поглощения, приведем ее к следующему виду:

.

Первые три терма инверсной функции изображены на карте Карно, показанной на рис. 11.12, в. Четвертый (временной) терм не может быть представлен на этой же карте.

На карте Карно для инверсной функции можно видеть, что нули в ячейках 1001 и 1011 являются смежными для нулей в ячейках 0001 и 0011, соответственно, и не покрываются одной и той же первичной импликантой. Статический 0-риск устраняется включением дополнительной первичной импликанты для покрытия этих четырех ячеек. Этот терм следует добавить к инверсной функции, которая затем повторно инвертируется для получения функции в гарантированном от риска виде.

Анализ схемы, приведенной на рис. 11.12, а, показывает, что в ней могут возникать ситуации риска обоих видов. На практике целесообразнее было бы провести преобразование схемы при помощи карты Карно, показанной на рис. 11.12, б, которая для удобства повторена на рис. 11.12, г. На этой карте функция упрощена таким способом, что в результате получилась гарантированная от статического 1-риска функция. Она имеет следующий вид:

.

Теперь осталось только проверить изображение на карте Карно инверсной функции для выявления 0-риска. Инверсная функция имеет вид

.

Она изображена на рис. 11.12, д. Поскольку на этой карте Карно нет смежных нулей, не покрытых одной и той же первичной импликантой, то нет и статического 0-риска, и функция является гарантированной также и от этого типа риска.