11.4. Возникновение ситуаций статического риска в комбинационных схемах

При изменении входных сигналов комбинационной схемы на ее выходе могут возникнуть выбросы. Они появляются из-за того, что на различных путях прохождения сигналов через схему от входа к ее выходу могут возникать различные временные задержки. Например, булева функция вида

может быть реализована с помощью изображенной на рис. 11.5 схемы из элементов И-НЕ. Сигналы через эту схему проходят по двум путям: первый - через элементы g₁, g₂ и g₃ и второй - через g₄ и g₃. Если считать, что все элементы имеют одинаковую временную задержку, равную t_g с, то очевидно, что задержка, возникающая на первом пути, больше задержки на втором.

Н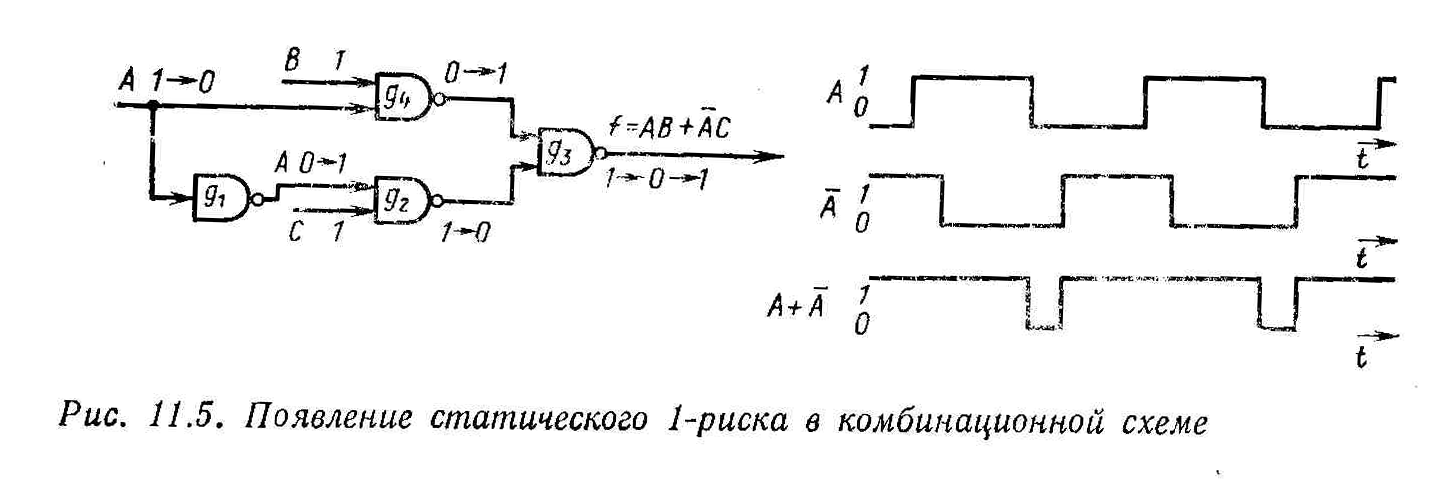 а рис. 11.5 показаны изменения, происходящие в схеме при условии, что В = 1 и С = 1, а А изменяется от 1 до 0. В случае указанного изменения сигнала А выход элемента g₄ изменяется от 0 до 1 и вызывает изменение выхода элемента g₃ от 1 до 0. На другом пути через схему сначала происходит изменение на выходе элемента g₁ от 0 до 1, вследствие которого изменяется выходной сигнал у элемента g₂ от 1 до 0, что приводит к изменению сигнала на выходе элементе g₃ от 0 до 1. Поскольку путь через g₄ и g₃ имеет меньшее время задержки, очевидно, что сигнал, проходящий поэтому пути, попадет на выход схемы раньше сигнала, распространяющегося по пути g₁, g₂, g₃ .

Поскольку было принято, что В = 1 и С = 1, уравнение схемы упрощается до выражения и при этом появляется вероятность возникновения статического 1-риска. Временная диаграмма, изображенная на рис. 11.5, показывает, что в выбранном примере в течение короткого периода времени, следующего за моментом изменения А из 1 в 0, сигналы А и равны одновременно 0 и, следовательно, . Поэтому в начале этого интервале времени сигнал изменяется из 1 в 0, возвращаясь назад, когда изменяется из 0 в 1. Схема генерирует статический 1-риск. На рис. 11.5 показано возникновение отрицательных выбросов. Наличие их подтверждает полученный в результате изучения структуры схемы вывод, заключающийся в том, что последовательность переходов выходного сигнала имеет вид 1  0  1. Функция, двойственная к функции , имеет вид

.

Н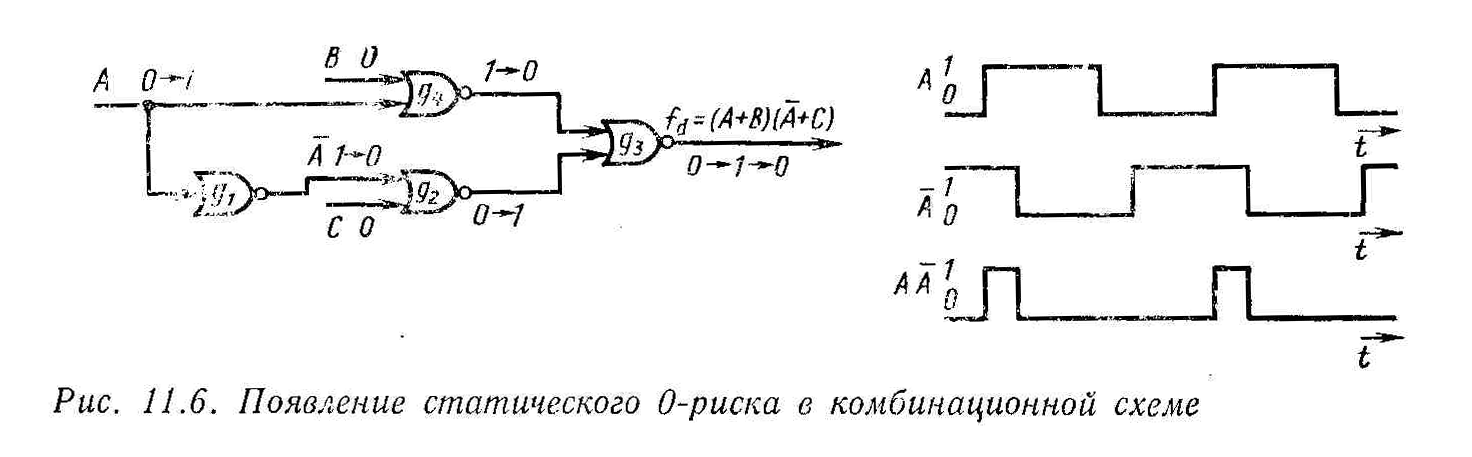 а рис. 11.6 показано, как можно реализовать это равенство с помощью элементов ИЛИ-НЕ. При условии, что В = 0 и С = О уравнение этой схемы упрощается до вида . Если можно выполнить такое упрощение, появляется вероятность статического 0-риска для схемы, реализующей уравнение . Сразу после изменения А из 0 в 1 сигналы А и одновременно равны 1 и, следовательно, . Это значение остается до тех пор, пока сигнал А не станет равным 0 и вновь не восстановится значение равное 0.

Изменения сигналов в схеме также показаны на рис. 11.6 при условии, что В = С = 0, а сигнал А изменяется из 0 в 1. Если все элементы схемы имеют одинаковую временную задержку, равную t_g, то путь g₄, g₃ имеет минимальное время задержки, и изменение А от 0 до 1 достигнет выхода по этому пути быстрее, чем по пути g₁, g₂, g₃, что приведет к изменению на выходе от 0 до 1. Когда то же самое изменение сигнала А попадет на выход схемы по другому пути, то выходной сигнал станет равен 0.