4.2 Создание модели в AnyLogic

Создаем блок-схему модели продуктового магазина из элементов библиотеки Enterprise Library (рисунок 4).

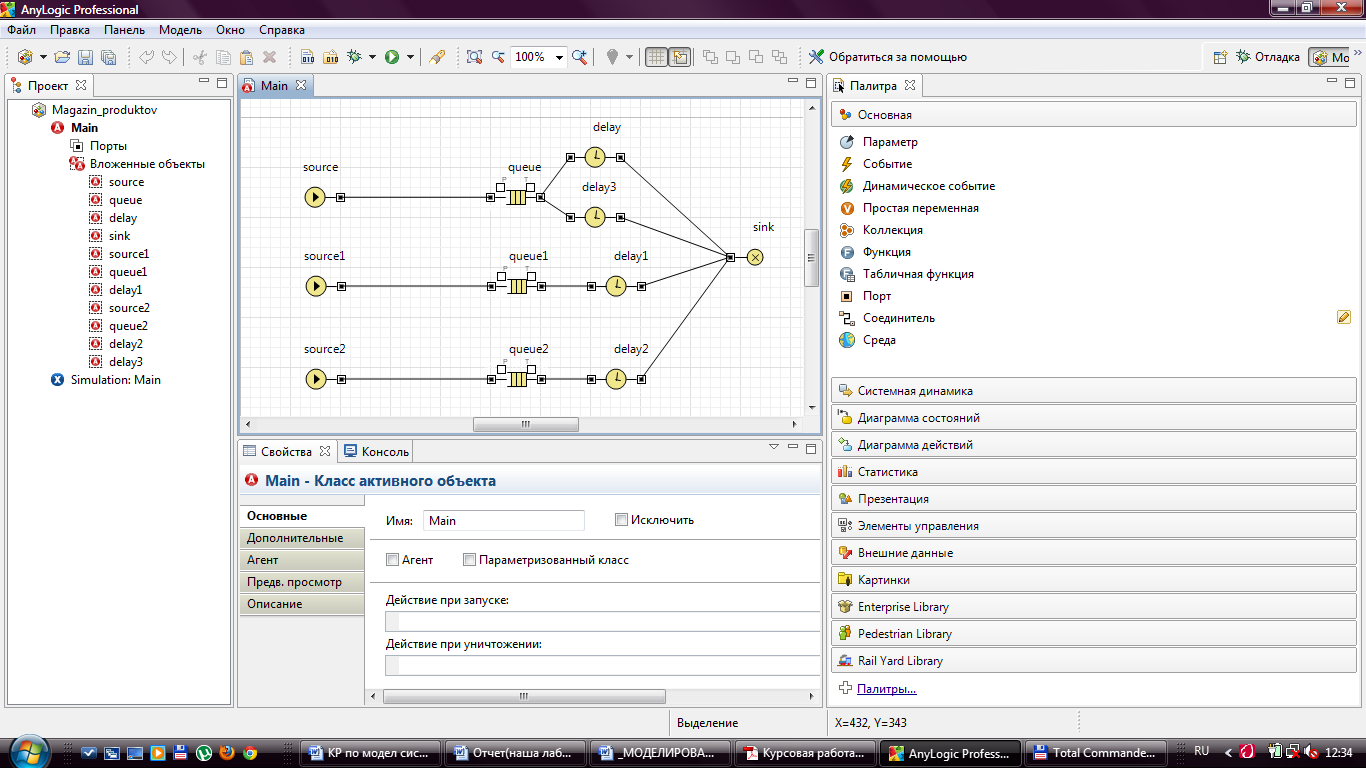
Рисунок 4 - Схема модели магазина в AnyLogic

Объекты Queue моделируют очереди из покупателей, ожидающих обслуживания.

Объект Source.

Представляет собой источник заявок. Обычно используется в качестве начальной точки потока заявок. Генерирует заявки любых подклассов базового класса Entity через случайные промежутки времени. Время генерации может как подчиняться закону распределения, так и определяться заданным нами расписанием. В нашем случае время генерации прихода покупателей в магазин задается экспоненциальном законом распределения с заданным значением математического ожидания. Зададим следующие свойства объектов Source:

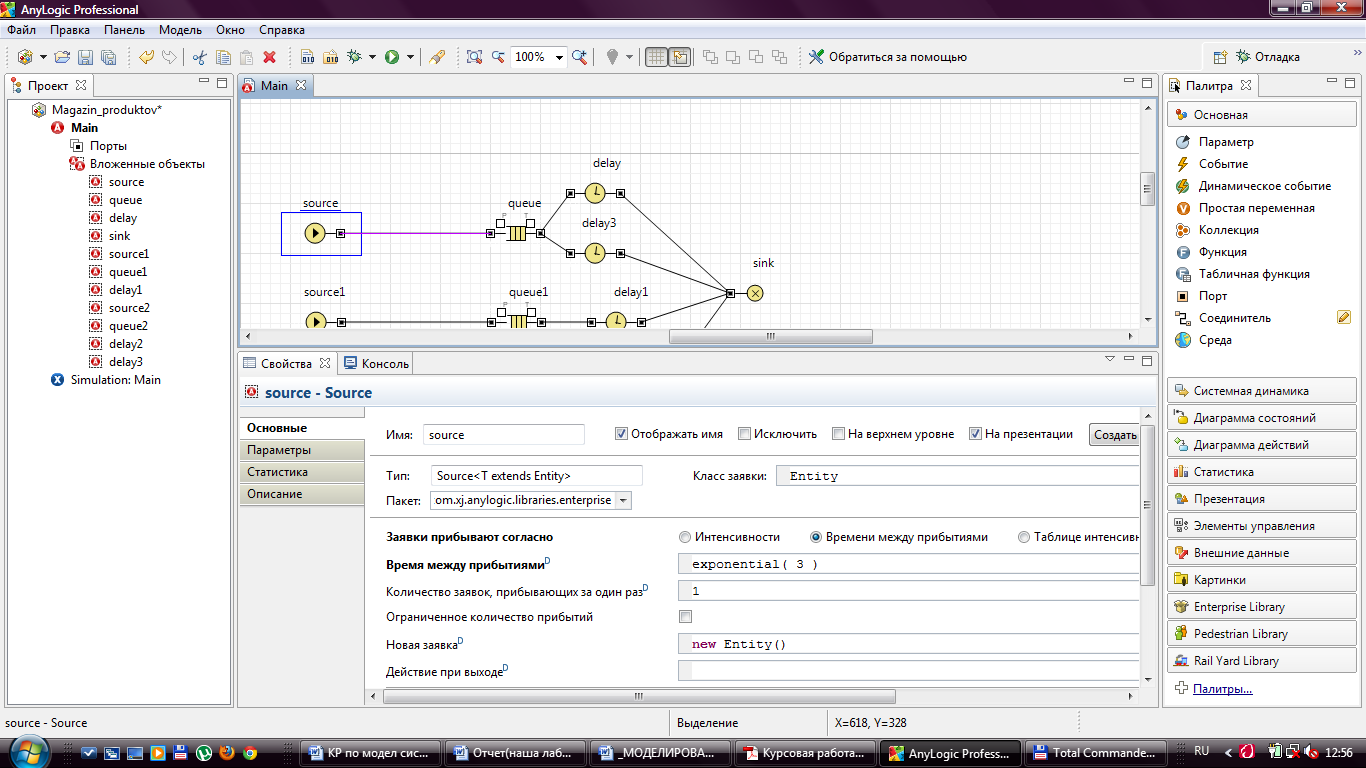
Рисунок 5 - Задание свойств объекта Source

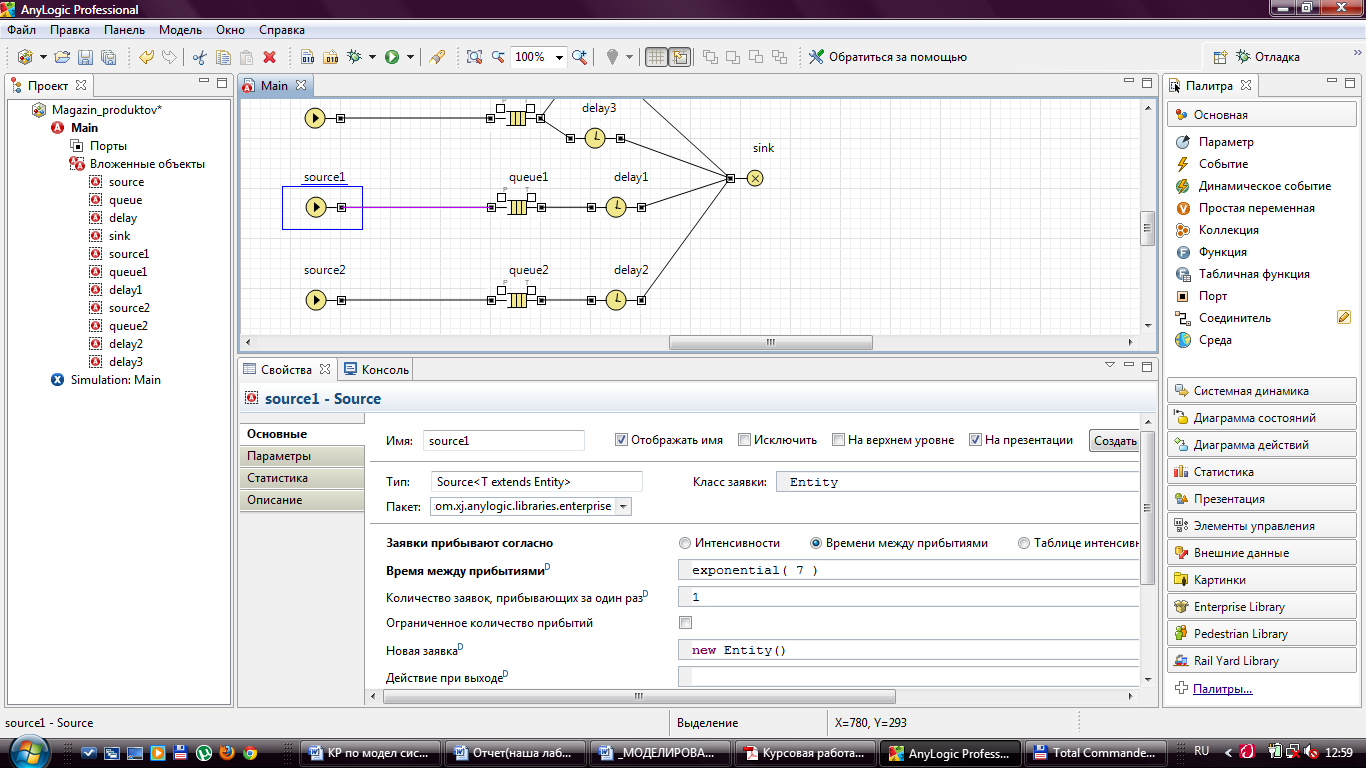
Рисунок 6 - Задание свойств объекта Source1

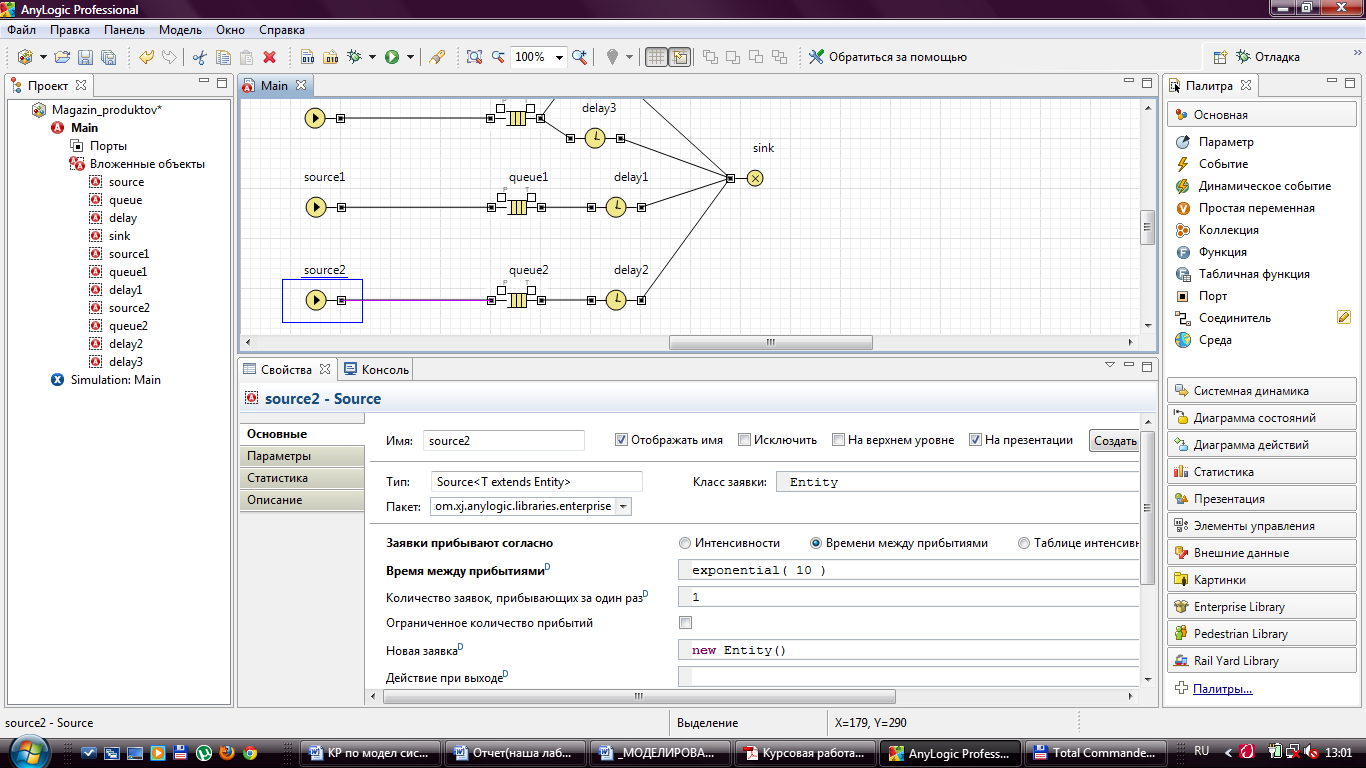
Рисунок 7 - Задание свойств объекта Source2

Объект Delay.

Задерживает заявки на заданное время. Как только время задержки истекает, заявка тут же покидает объект. Если объект Delay занят обслуживанием заявки, то новую заявку он не примет.

В построенной схеме модели магазина объекты Delay и Delay3 – это 2 продавца отдела №1. Объект Delay – это отдел №2. Delay – это отдел №3.

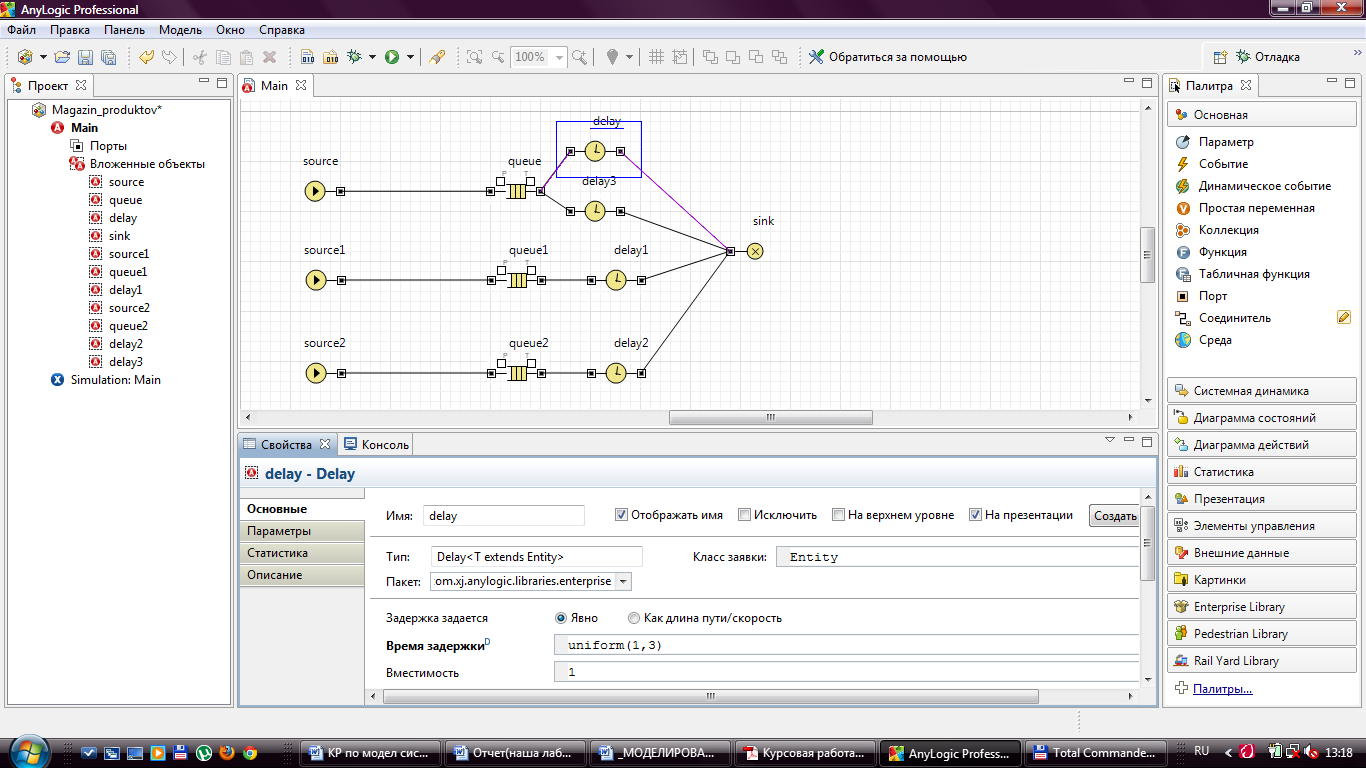
Рисунок 8 - Задание свойств объекта Delay

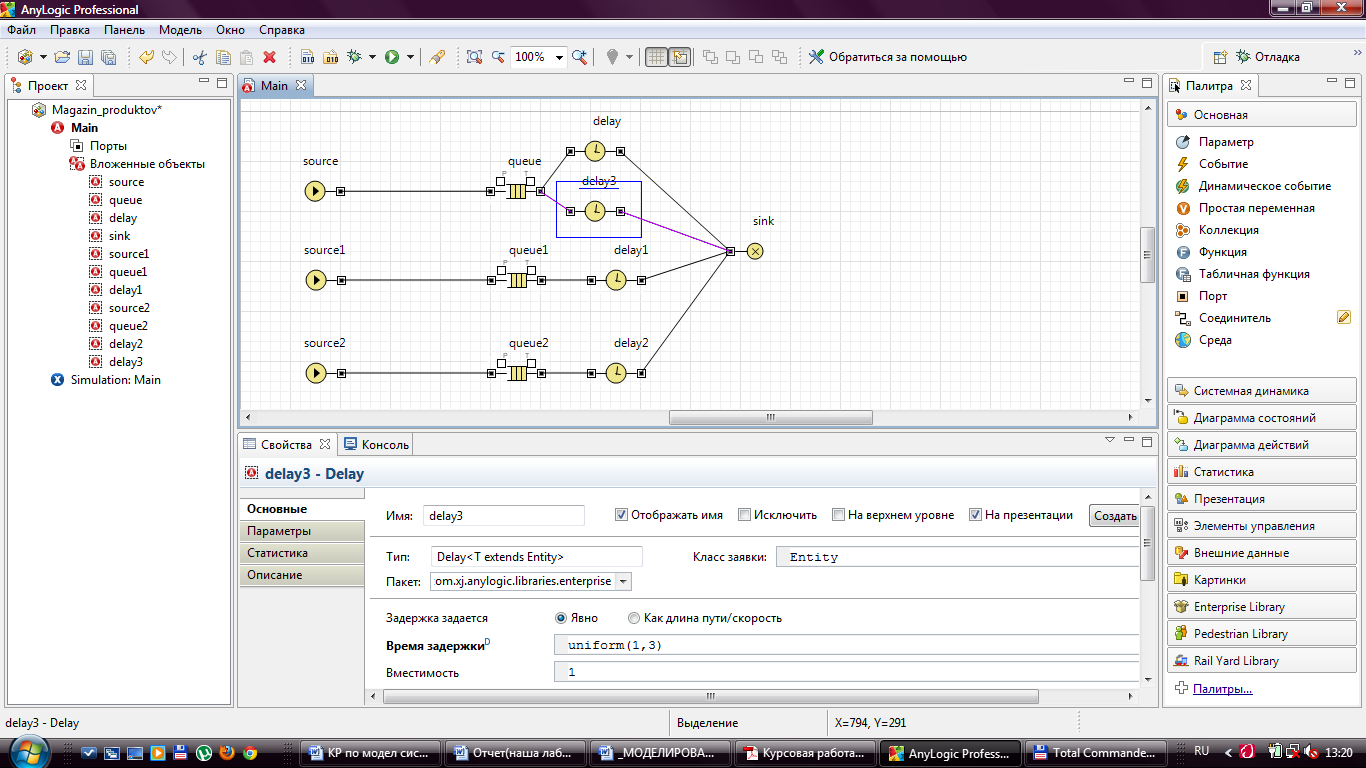
Рисунок 9 - Задание свойств объекта Delay3

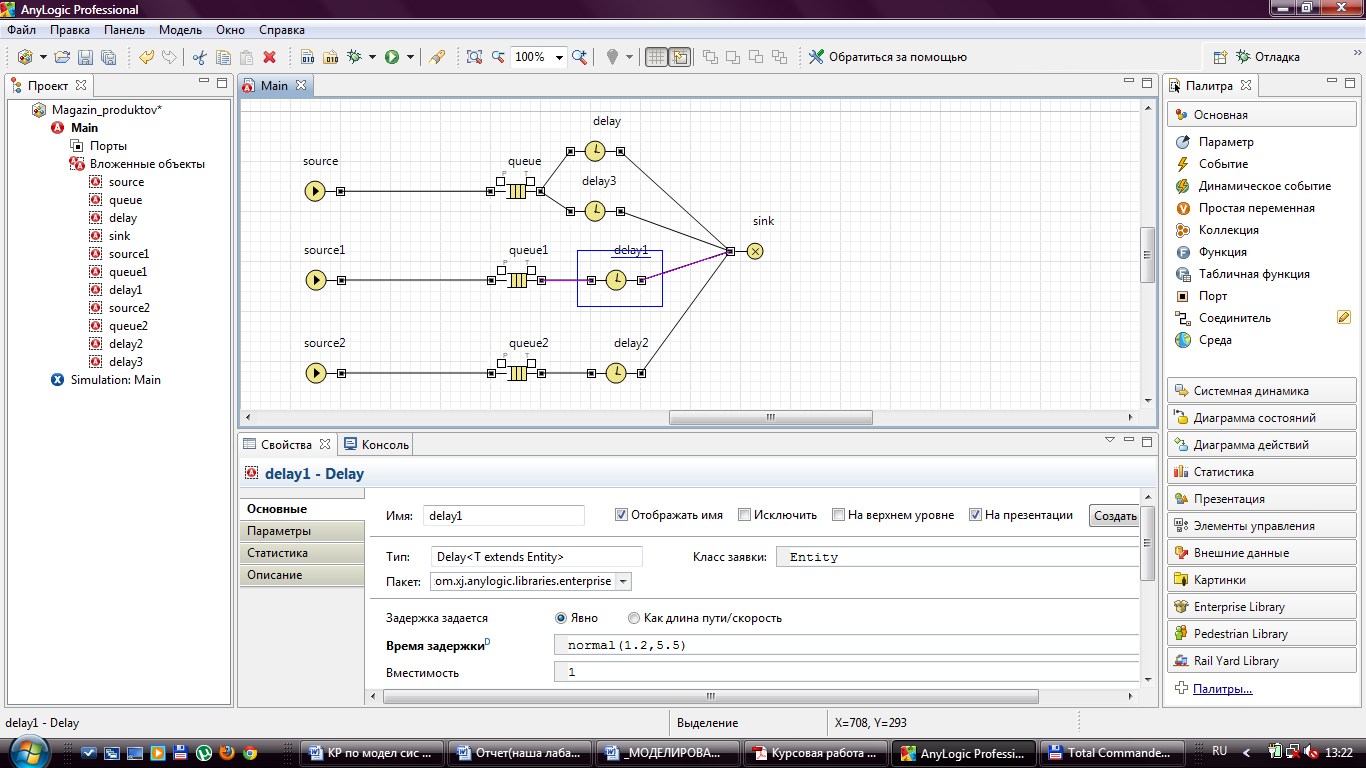
Рисунок 10 - Задание свойств объекта Delay1

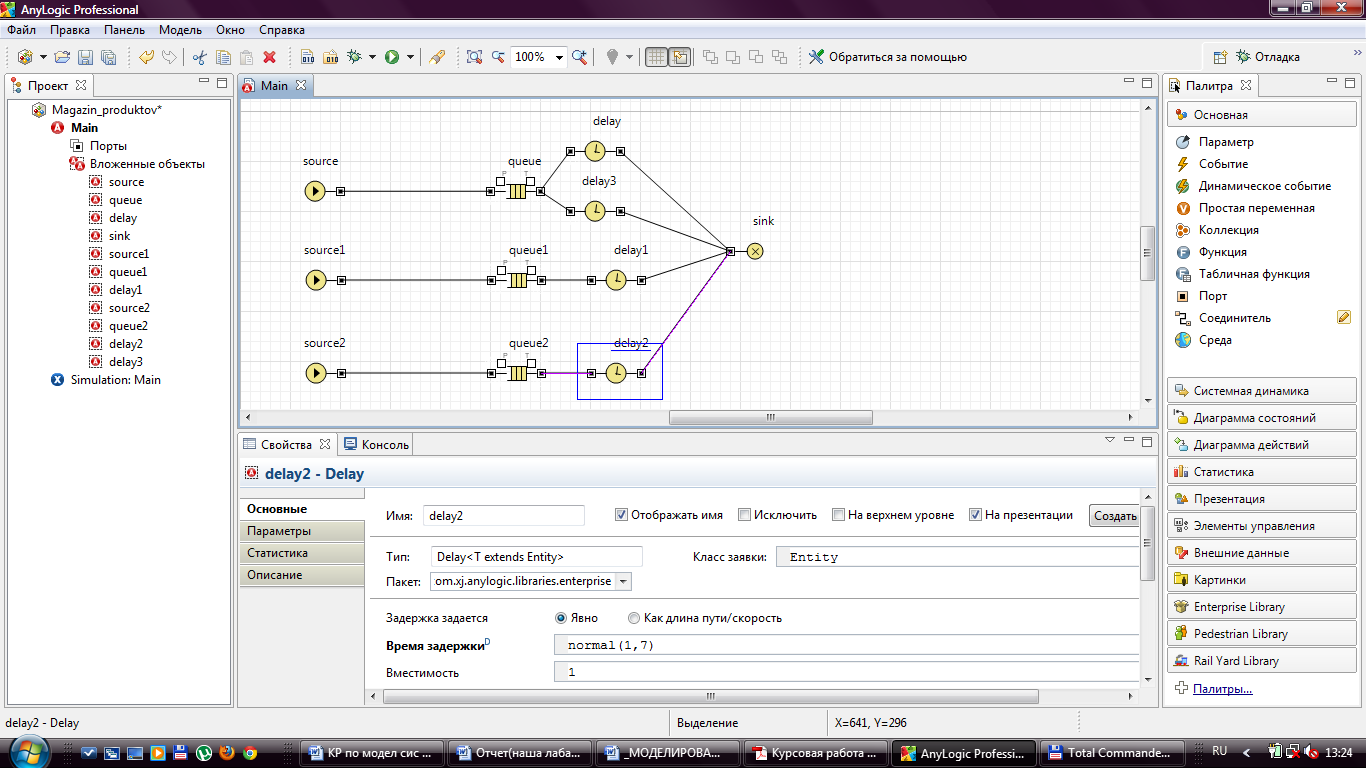
Рисунок 11 - Задание свойств объекта Delay2

Объект Sink.

Уничтожает поступившие заявки. Обычно используется в качестве конечной точки потока заявок.

Состояние модели, полученное в процессе ее работы, показано на рис.12.

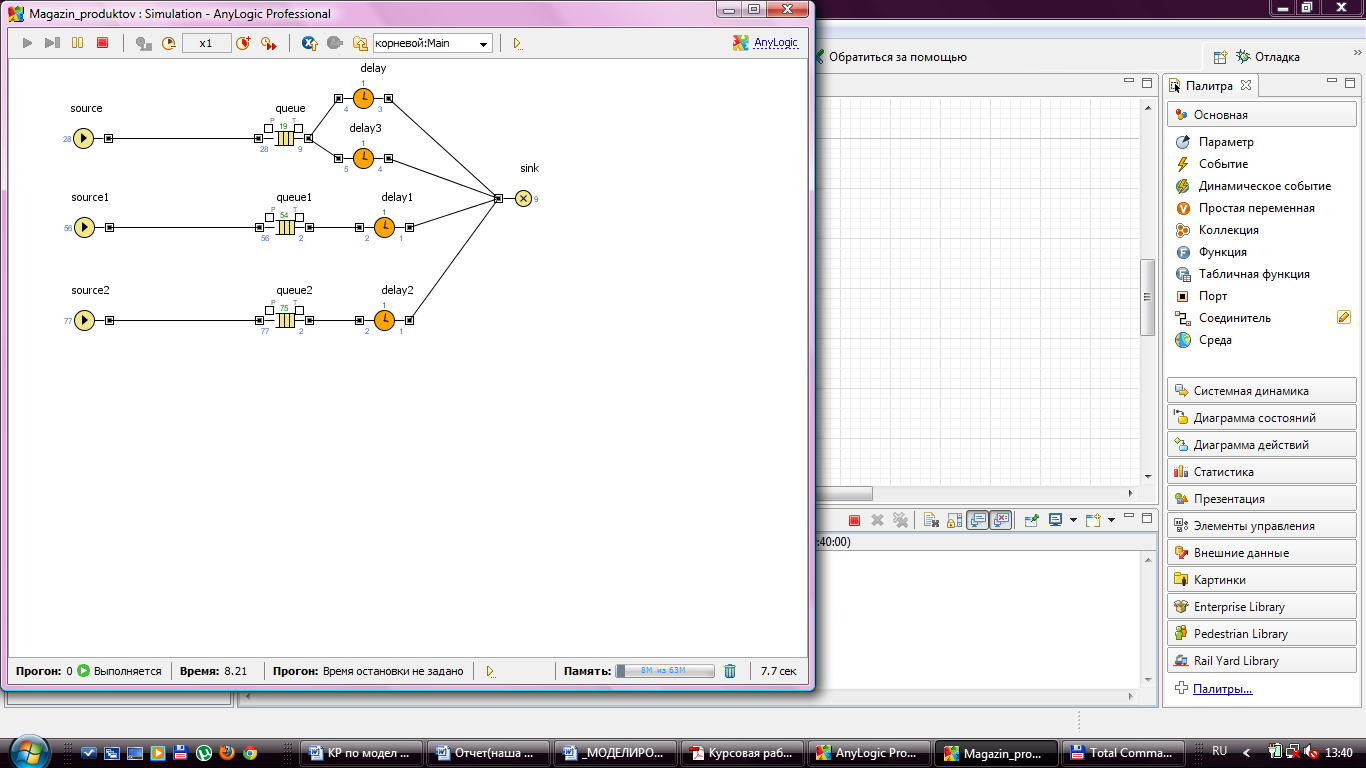
Рисунок 12 - Окно запуска программы

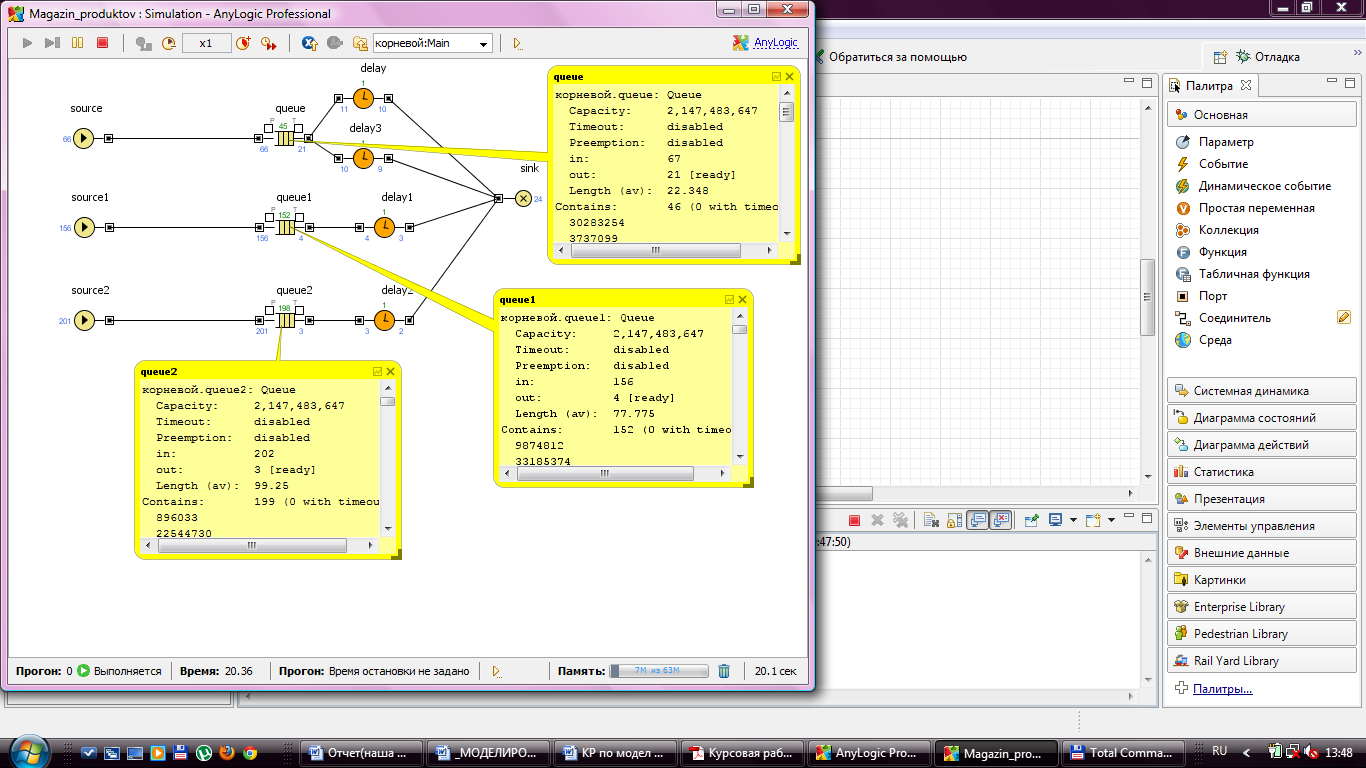
Рисунок 13 - Модель с окнами инспектов

4.3 Результаты вычислительных экспериментов

Для рассматриваемого примера получены статистические данные по загрузке приборов. Результаты проведения 7 испытаний представлены в таблице 4.

Таблица 4 – Зависимость коэффициентов загрузки приборов от объема выборки

№	Объем выборки	RBREAD	RSAUSAGE	RMACARONI
1	50	0,310	0,805	0,499
2	100	0,426	0,711	0,513
3	300	0,445	0,888	0,676
4	600	0,377	0,759	0,738
5	1000	0,346	0,784	0,722
6	4000	0,321	0,745	0,737
7	10000	0,429	0,713	0,685

На основании этих данных построен график зависимости коэффициента загрузки прибора от количества заявок, показанный на рис.14.

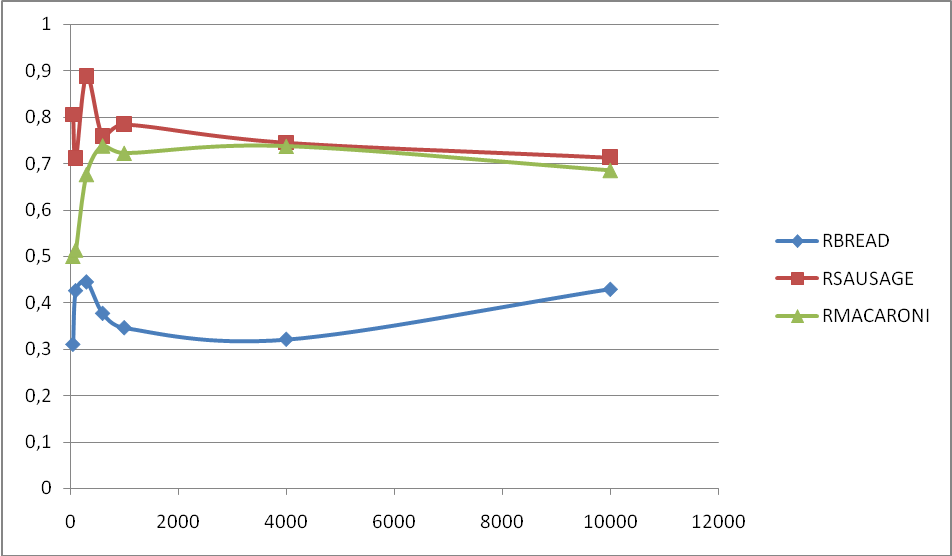
Рисунок 14 - График зависимости коэффициента загрузки прибора

от объема выборки

Сравнив полученные графики (рисунки 2 и 14), увидели, что они приблизительно похожи. Из чего можно сделать вывод о том, что модели составлены правильно.

Заключение

В данной курсовой работе на основе полученного задания были разработаны модели в среде GPSS и в AnyLogic. С моделями были проведены вычислительные эксперименты. На основе этих экспериментов была получены статистические выборки и построен график, который наглядно демонстрирует зависимость коэффициента загрузки от объема выборки.

Выводы, полученные при моделировании системы массового обслуживания, отражают основные особенности функционирования объекта и позволяют качественно и количественно оценить его поведение.

УКАЗАТЬ КОНКРЕТНО ВЫВОДЫ ДЛЯ МАГАЗИНА ( КАК ЗАГРУЖЕНЫ ПРОДАВЦЫ ДЛЯ РАЗНЫХ ОТДЕЛОВ, КАК ДОЛГО ЖДУТ ПОКУПАТЕЛИ, ЧТО МОЖНО СДЕЛАТЬ ДОЛЯ УЛУЧШЕНИЯ КАЧЕСТВА ОБСЛУЖИВАНИЯ ПОКАПАТЕЛЕЙ?