Электрическая цепь с последовательным соединением r, l и c элементов

Рассмотрим общий случай последовательного соединения резистора, катушки индуктивности и конденсатора (Рис.1).

На основании 2-го закона Кирхгофа

(1)

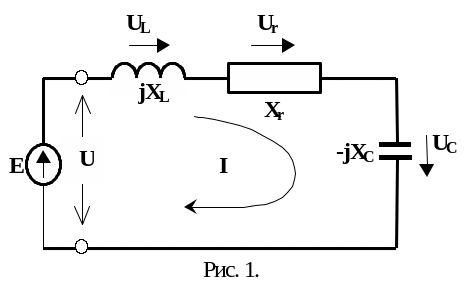
Учитывая закон Ома, имеем

Теперь уравнение (1) можно записать в виде

или

,

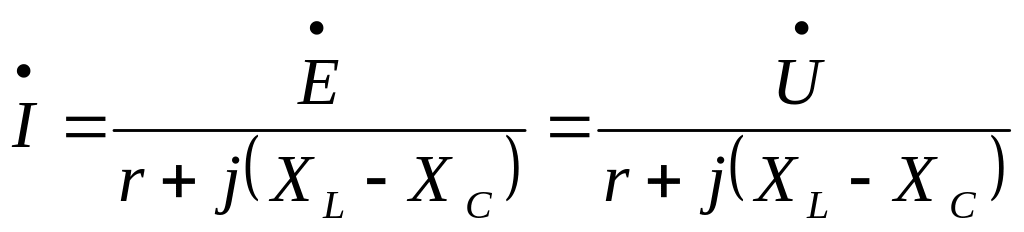где - напряжение между выводами неразветвленной цепи.

Величина называется комплексным сопротивлением неразветвленной цепи.

или ,

где модуль комплексного сопротивления, или полное сопротивление цепи;

- аргумент комплексного числа.

В зависимости от знака величины аргумент комплексного сопротивления может быть либо положительным (индуктивный характер), либо отрицательным (емкостной характер).

РЕЗОНАНС НАПРЯЖЕНИЙ

Режим электрической цепи при последовательном соединении участков с индуктивностью и емкостью, характеризующийся равенством индуктивного и емкостного сопротивлений, называется резонансом напряжений.

Реактивные сопротивления и (Рис. 3) зависят от частоты вынужденных колебаний ω:

.

При резонансе напряжений

Отсюда определяется резонансная частота

Резонанс в цепи можно установить двумя путями: изменением параметров L и С (одного из них или обоих вместе) при постоянной частоте источника или изменением частоты источника энергии при постоянных L и С.

При увеличении частоты увеличивается пропорционально частоте, а уменьшается по закону обратной пропорциональности.

Соответственно полное сопротивление Z цепи при резонансной частоте ω_Р оказывается наименьшим, равным активному сопротивлению r; при частотах ω < ω_Р полное сопротивление увеличивается с уменьшением частоты за счет роста ; при частотах ω > ω_Р полное сопротивление увеличивается с уменьшением частоты за счет роста .

Физическая причина возникновения повышенных напряжений – колебания значительной энергии, запасаемой попеременно в электрическом поле конденсатора и в магнитном поле индуктивного элементов.

Резонанс напряжений может быть опасен в установках сильного тока, где его возникновение специально не предусматривается.

При резонансе напряжений отношение напряжения на катушке индуктивности или конденсатора к напряжению источника равно отношению волнового сопротивления Z_В (характеристическое сопротивление колебательного контура) к активному. Действительно, при резонансе сопротивления реактивных элементов

.

Поэтому

.

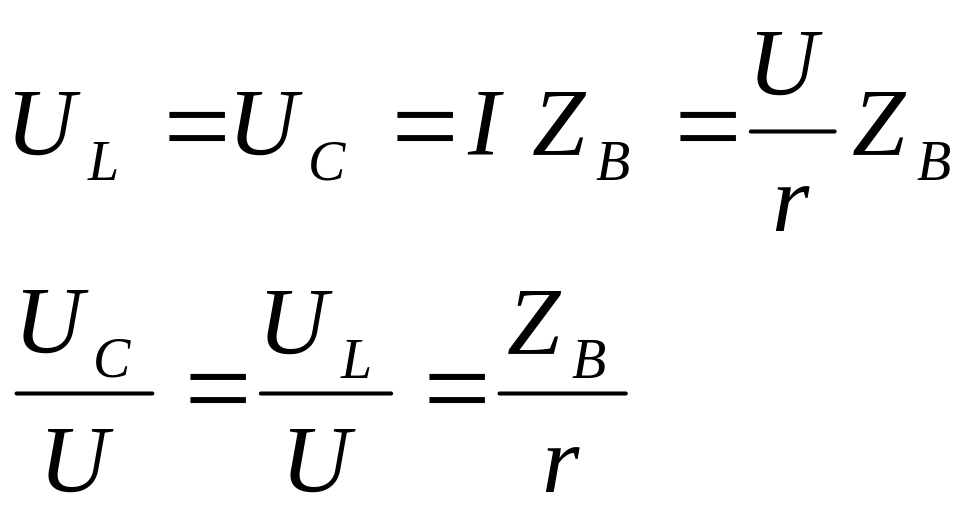Из этого выражения следует, что при Z_В > r напряжение на реактивных элементах больше напряжения питания. Такое превышение может оказаться значительным, если реактивные сопротивления много больше активного, и изоляция катушки или конденсатора может быть пробита.

Резонансные явления широко применяются в радиотехнике. Качество резонансного контура считается тем выше, чем больше отношение , которое получило название добротности контура Q;

.

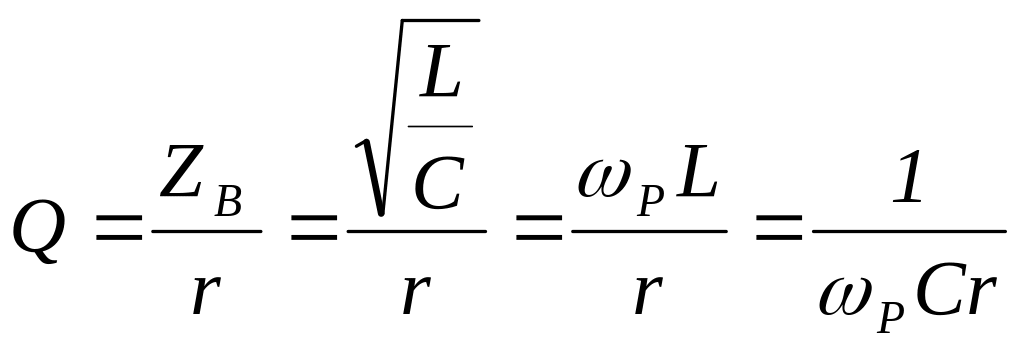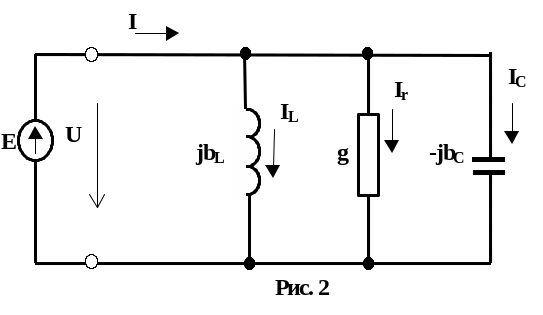
Электрическая цепь с параллельным соединением ветвей

(Лаб. раб.№3, стр. 3-6)

На рис. 1 представлена электрическая цепь с параллельным соединением резистивного, индуктивного и емкостного элементов. Будем считать заданными проводимость резистивного элемента и комплексные проводимости индуктивного - и емкостного элементов. Принципиальной особенностью электрических цепей с параллельным соединением элементов является то, что напряжение на каждом из них одинаковое, т.е. у параллельных ветвей общее напряжение.

(1)

По первому закону Кирхгофа

. (2)

В соответствии с законом Ома комплексные значения токов в ветвях, согласно рис. 2, будут определяться следующим выражением

. (3)

Сумма комплексных проводимостей всех параллельных ветвей в выражении (2) равна комплексной проводимости данной цепи

. (4)

В показательной форме комплексная проводимость равна

, (5)

где - модуль, а - аргумент комплексной проводимости цепи.

В тригонометрической форме

. (6)

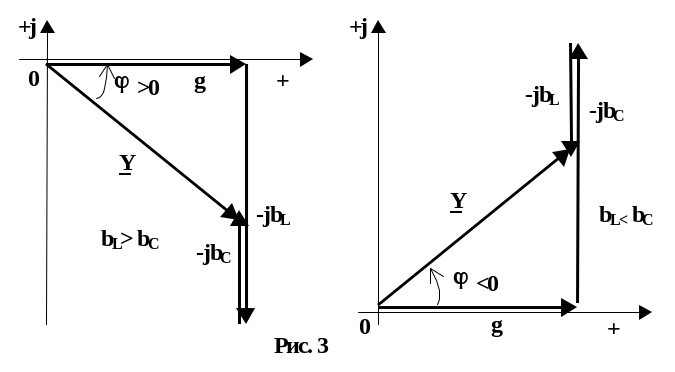
На комплексной плоскости слагаемые комплексной проводимости цепи изображены в виде векторов для двух случаев и (Рис. 3).

В первом случае комплексная проводимость цепи имеет индуктивный характер, во втором - емкостной.

Подставив значение комплексной проводимости в показательной форме (5) во (2), получим комплексное значение тока в виде

(7)

Из (7) следует, что действующее значение тока в неразветвленной части цепи

.

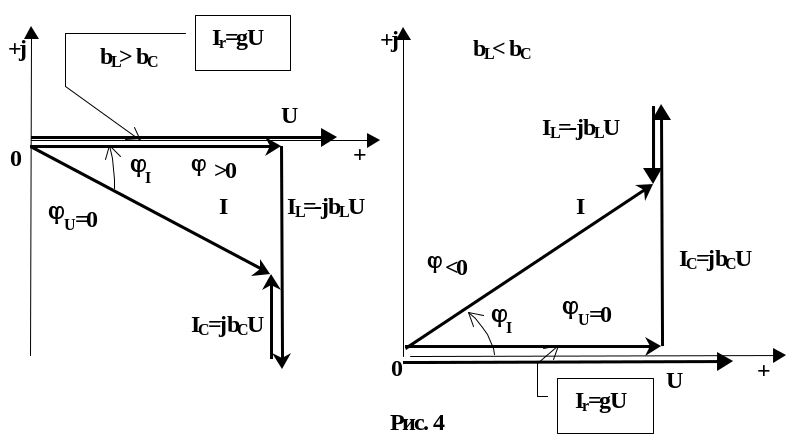
На комплексной плоскости представлены векторные диаграммы напряжения и токов для двух случаев и (Рис. 4) при одинаковом напряжении .

Если комплексная проводимость цепи имеет индуктивный характер, то общий ток (в неразветвленной части цепи) отстает по фазе от напряжения.

Комплексная мощность анализируемой цепи

.

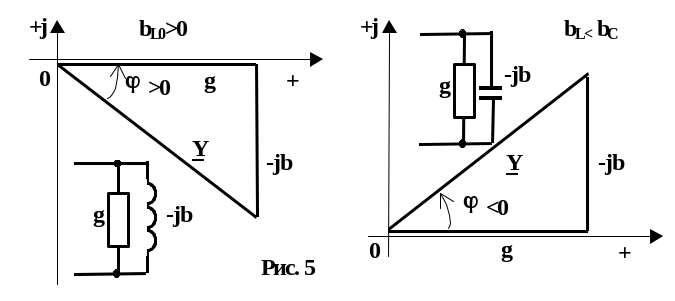
Если электрическая цепь содержит несколько резистивных, индуктивных и емкостных элементов, включенных параллельно, то комплексная проводимость

(8)

где g - активная проводимость цепи; b - реактивная проводимость цепи.

Выражению (8) соответствуют треугольники проводимостей на комплексной плоскости (Рис. 5).