
- •Вопрос 1. Определение двойных и повторных пределов. Теорема о связи между двойными и повторными пределами.
- •Вопрос 2. Определение непрерывности по совокупности и в отдельности по каждому переменному. Теорема о связи непрерывности по совокупности и по отдельной переменной.
- •Вопрос 3. Определение частной производной. Определение дифференцируемой функции и градиента. Теорема о непрерывности дифференцируемой функции.
- •Вопрос 4. Теорема о необходимом условии дифференцируемости функции. Следствие (связь с градиентом)
made by gr.417 at Radiophysical faculty, NNSU (2004) (c)http://rf-nnsu.narod.ru
Вопрос 1. Определение двойных и повторных пределов. Теорема о связи между двойными и повторными пределами.
Определение.
Пусть
![]() - функция двух независимых переменных,
- функция двух независимых переменных,
![]() и точка
и точка
![]() - предельная точка множества
- предельная точка множества
![]() ,
тогда 1) В смысле метрики пространства
,
тогда 1) В смысле метрики пространства
![]() ,
,
![]() при
при
![]() - это двойной предел, 2) Если при
- это двойной предел, 2) Если при
![]() существует
существует
![]() и существует
и существует
![]() ,
то предел
,
то предел
![]() называется повторным пределом. Аналогично
предел
называется повторным пределом. Аналогично
предел
![]() .
.
Теорема (о связи
между двойным и повторным пределом).
Пусть для
выполнены условия: 1)
![]() ,
,
![]() - предельная точка множества
.
2) При
- предельная точка множества
.
2) При
![]() существует конечный предел
существует конечный предел
![]() ,
тогда существует повторный предел
и он равен двойному. Доказательство.
Пусть для определенности предел двойной
существует и он конечный
,
тогда существует повторный предел
и он равен двойному. Доказательство.
Пусть для определенности предел двойной
существует и он конечный
![]()
![]() .
.
![]() ,
,
![]() ,
,
![]() - очевидно, что неравенство выполняется
если одновременно
- очевидно, что неравенство выполняется
если одновременно
![]() и
и
![]() .
.
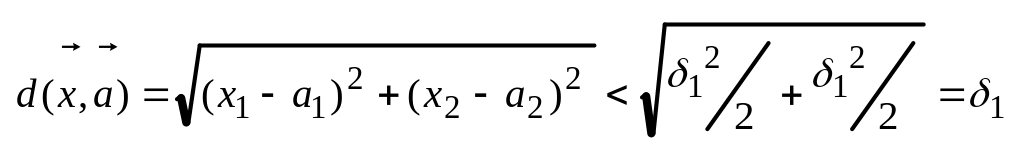 .
Из того, что существует конечный предел
при
.
Из того, что существует конечный предел
при
![]() .
Выберем
.
Выберем
![]() .
Составим разность
.
Составим разность
![]() ,
тогда
,
тогда
![]() .
.
Вопрос 2. Определение непрерывности по совокупности и в отдельности по каждому переменному. Теорема о связи непрерывности по совокупности и по отдельной переменной.
Определение.
Пусть функция
![]() ,
тогда 1) Функция
,
тогда 1) Функция
![]() непрерывная в точке
непрерывная в точке
![]() называется непрерывной по совокупности
переменных в этой точке если
называется непрерывной по совокупности
переменных в этой точке если
![]() .
2) Функция
непрерывная в точке
называется непрерывной по переменной
.
2) Функция
непрерывная в точке
называется непрерывной по переменной
![]() в этой точке если
в этой точке если
![]() .
Другими словами функция
.
Другими словами функция
![]() непрерывна по переменной
в точке
непрерывна по переменной
в точке
![]() если она непрерывна по этой переменной
как функция одной переменной при
фиксированных других переменных, равных
координатам.
если она непрерывна по этой переменной
как функция одной переменной при
фиксированных других переменных, равных
координатам.
Теорема (о связи
непрерывности по совокупности и в
отдельности по каждой переменной).
Пусть
![]() непрерывна в
непрерывна в
![]() по совокупности переменных, то она
непрерывна в этой точке в частности по
каждой переменной; обратное утверждение
в общем случае неверно, т.е. существует
функция непрерывная в
по каждой переменной, но разрывная по
совокупности переменных. Доказательство.
Пусть
непрерывна в точке
,
т.е.
по совокупности переменных, то она
непрерывна в этой точке в частности по
каждой переменной; обратное утверждение
в общем случае неверно, т.е. существует
функция непрерывная в
по каждой переменной, но разрывная по
совокупности переменных. Доказательство.
Пусть
непрерывна в точке
,
т.е.
![]() ,
положим
,
положим
![]() ,
тогда с учетом того, что
,
тогда с учетом того, что
![]() и |Δf(x0)|=Δif(x0)
имеем
.
Второе докажем при помощи примера.
,
.
и |Δf(x0)|=Δif(x0)
имеем
.
Второе докажем при помощи примера.
,
.
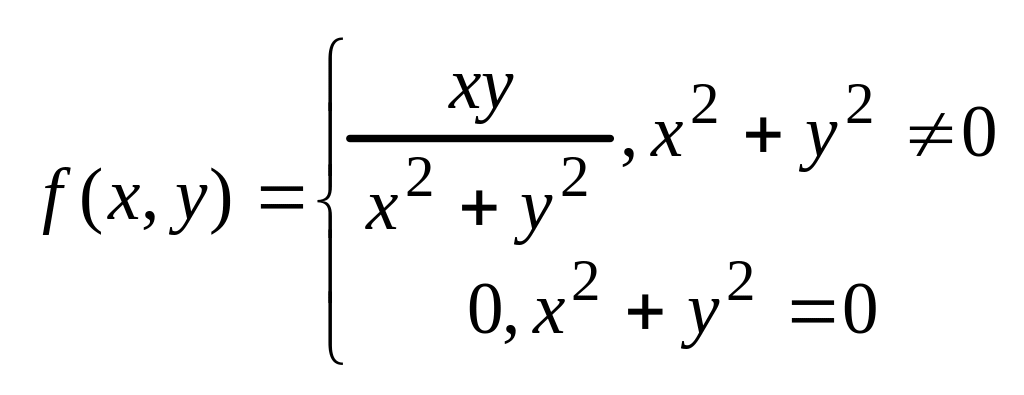 данная функция непрерывна в точке (0,0)
в отдельности по каждой переменной:
данная функция непрерывна в точке (0,0)
в отдельности по каждой переменной:
![]() - непрерывна,
- непрерывна,
![]() - непрерывна.
- непрерывна.
![]() при
при
![]() равен
равен
![]() - функция не непрерывна, т.к. предел не
равен значению функции в этой точке.
- функция не непрерывна, т.к. предел не
равен значению функции в этой точке.
Вопрос 3. Определение частной производной. Определение дифференцируемой функции и градиента. Теорема о непрерывности дифференцируемой функции.
Определение:
Пусть функция
![]() - функция k
переменных
- функция k
переменных
![]() ;
;
![]() ,
положим
,
положим
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
если предел этого отношения существует,
то его называют частной производной
функции
в точке
,
если предел этого отношения существует,
то его называют частной производной
функции
в точке
![]() .
.
![]()
![]() .
.
Определение.
Пусть функция
- функция k
переменных дифференцируема в точке
если ее полное приращение в этой точке
можно представить в виде:
![]() ,
,
![]() ;
;
![]() ,
где
,
где
![]() при
при
![]() .
.
![]() - градиент функции
в точке
(обозначается
- градиент функции
в точке
(обозначается
![]() ).
).
Теорема (о
непрерывности дифференцируемой функции).
Пусть
дифференцируема в
![]() ,
тогда эта функция непрерывна в этой
точке, обратное утверждение не верно.
Доказательство.
1) Пусть
дифференцируема в
,
,
тогда эта функция непрерывна в этой
точке, обратное утверждение не верно.
Доказательство.
1) Пусть
дифференцируема в
,
![]() ,
,
![]() ,
,
![]() .
.
![]()
![]() ,
непрерывна в
.
2)
,
непрерывна в
.
2)
![]() непрерывна
в
непрерывна
в
![]() ,
но не дифференцируема в этой точке, т.к.
ее приращ-е Δ
,
но не дифференцируема в этой точке, т.к.
ее приращ-е Δ![]() не м. быть записано в виде
не м. быть записано в виде
![]()
