2. 3. Дифференцирование функций, заданных параметрически

Если функция задана параметрически двумя уравнениями , , , то ее производные вычисляются по формулам:

, .

Примечание. Производные по аргументу иногда, следуя Исааку Ньютону, обозначают точками наверху: , , . В этих обозначениях формулы, по которым находятся производные параметрически заданной функции, принимают вид:

, .

Пример3. Найти и , если функция задана параметрически:

.

Решение. Последовательно находим: , ; ;

; , .

2. 4. Дифференцирование неявных функций

Говорят, что уравнение задает неявно функцию , на интервале , если для всех выполняется равенство .

Для вычисления производной функции следует продифференцировать по x тождество , помня, что есть функция от , а затем полученное уравнение разрешить относительно .

Пример 4. Найти значение в точке для функции, заданной неявно уравнением .

Решение. Продифференцируем обе части уравнения по (не забываем, что зависит от ):

, ,

, .

2. 5. Правило Лопиталя

1. При раскрытии неопределенностей кроме классических методов вычисления пределов, рассмотренных ранее, во многих случаях можно пользоваться правилом Лопиталя - Бернулли:

если или и существует предел отношения их производных , то .

Это правило справедливо и в случае .

Пример 5. .

Пример 6. .

Здесь мы дважды применили правило Лопиталя и воспользовались первым замечательным пределом.

Пример 7. .

2. При раскрытии неопределенностей для применения правила Лопиталя, данное выражение надо преобразовать в отношение двух функций (в неопределенность или ).

Пример 8. .

Пример 9.

.

3. При раскрытии неопределенностей ; ; рекомендуется найти предварительно предел логарифма искомой функции.

Пример 10. .

Решение. Введем обозначение , тогда .

.

Так как .

2. 6. Исследование функции и построение ее графика

Для построения графика функции сначала проводим элементарное исследование: находим область определения, асимптоты, выясняем некоторые особенности функции (если они имеются), т. е. точки пересечения с осями координат, симметрия, периодичность. Затем, используя первую производную, находим интервалы монотонности, экстремумы, а по второй производной — интервалы выпуклости, точки перегиба.

Рекомендуется исследование сопровождать последовательным построением графика функции.

Пример 1. построить график функции .

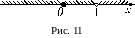Решение. 1. Область определения данной функции представляет собой множество (см. рис. 11).

2. Пределы функции в точках разрыва и на концах области определения (данная функция имеет одну точку разрыва):

; ; .

3. Асимптоты. Если , то прямая — вертикальная асимптота. В нашем случае вертикальная асимптота имеет уравнение . Прямая является наклонной асимптотой, если существуют конечные пределы

и .

Так как ; , то наклонная асимптота имеет уравнение .

Если , то — горизонтальная асимптота.

4. Точки пересечения графика с осями координат дают: во-первых, нули функции (чтобы их найти, необходимо решить уравнение ) и, во-вторых, значение , если . Так как для данной функции , то график проходит через точку О .

5. Симметрия. Функция – четная, если ; ее график симметричен относительно оси . Функция – нечетная, если ; ее график симметричен относительно начала координат. В нашем случае

; ,

т. е. и , следовательно, симметрии относительно осей координат у графика нет.

6. Периодичность. Если для некоторого числа выполняется равенство для всех , то функция – периодическая с периодом . Очевидно, наша функция не является периодической.

7. Находим первую производную: .

8. Находим критические точки ( т. е. точки, в которых или

не существует), отмечаем их на области определения функции (см. рис. 12) - получаем интервалы знакопостоянства производной :

.

В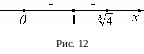 сюду в области определения первая производная существует.

9. Промежутки монотонности. Определяем знак производной в каждом интервале. Там, где , функция возрастает ( ); а там, где ,

о на убывает ( ).

Результаты исследования сводим в табл. 1

Таблица 1

		0	(0; 1)	1
	+	0	–		–	0	+

10. Экстремальные значения (если они есть):

.

11. Вторая производная: .

12. Интервалы знакопостоянства второй производной. Находим точки, в которых или не существует, отмечаем их на области определения функции (см. рис. 13). Получим интервалы знакопостоянства .

, .

Вторая производная существует для всех .

13. Промежутки выпуклости и вогнутости. Определяем знак производной в каждом интервале. Кривая является вогнутой при тех значениях аргумента , при которых (в окрестности точки вогнутости график располагается над касательной к нему в этой точке; в таблице интервал вогнутости будем обозначать символом ). Кривая в точке является выпуклой, если в этой точке (в этой точке график располагается под касательной и выпуклостью вверх ). Результаты сводим в табл. 2.

Таблица 2

				0		1
	+	0	–	0	–		+
		т. п.

14. Точки перегиба. Находим значение ,

тем самым определяем точку — точку перегиба. Касательная к графику в точке помогает уточнить, в каком направлении проходит в этой точке график. Поэтому полезно вычислить угловой коэффициент этой касательной: и провести в точке такую часть касательной (обычно около 1 сантиметра), которая делает ясным прохождение кривой в окрестности точки перегиба (см. рис. 14).

15. Строим график (если необходимо, находим несколько дополнительных точек).

Пример 2. Построить график функции .

Р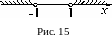 ешение. 1. Область определения данной функции представляет собой множество (см. рис. 15).

Функция определена и непрерывна вне отрезка .

2. ; , так как .

3. и — вертикальные асимптоты; — горизонтальная асимптота.

4. график не пересекает ось ; :

; ; , так как .

5. 6. нет.

7-10. для всех . Следовательно, функция возрастает на интервалах и .

11-14. ; имеет знак тот же, что и аргумент :

– выпуклость вниз, т. е. вогнутость ;

– выпуклость вверх . Точек перегиба нет.

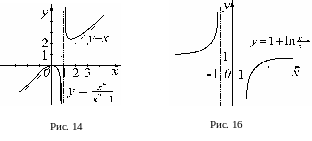15. Строим график (см. рис.16).

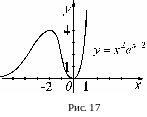Пример 3. Построить график функции .

Решение. Очевидно, , , для всех . Точек разрыва и вертикальных асимптот нет.

, так как ; , так как . Неопределенность раскрываем, дважды применив правило Лопиталя (см. 2.5.): — горизонтальная асимптота при .

Находим первую производную: . Ищем критические точки: , .

				0
	+	0	–	0	+

; ;

; ;

; .

	+	0	–	0	+
		т. п.		т. п.

; ;

; .

Найдем дополнительно значение функции при :

и построим ее график (см. рис.17).