5.4.1. Сферические волны, линза и зонная пластинка, элементы плоской оптики

Сферические волны являются решени1ем уравнений Максвелла вида:

, , где + для сходящейся, – для расходящейся. В параксиальном приближении . Отбрасывая все, что не зависит от x и y получим – распределение амплитуды сферической волны в плоскости на расст. z от центра.

Построим транспарант, преобразующий плоскую волну в сферическую. Профиль требуемого транспаранта: . Таким транспарантом является линза, у которой профиль имеет вид парабалоида. Функция пропускания будет иметь вид: – не зависит от типа линзы (вогнутая, выгнутая). Раскладываем на составляющие:

. В точке 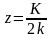формируется сходящаяся волна, в зеркальной (отн. транспаранта) точке – расходящаяся. Такой транспарант называется синусоидальной зонной пластинкой.

Призма – представляет собой прозрачную пластинку переменной толщины. Преобразует плоскую нормально падающую волну в плоскую наклонную. Линза –преобразует плоскую нормально падающую волну в сферическую. Синусоидальная дифракционная решетка – представляет собой амплитудный транспарант с коэффициентом пропускания в диапазоне 0…1. Формирует из плоской волны три (1 плоскую и 2 наклонные). Синусоидальная зонная пластинка – формирует из плоской волны три (1 плоскую и 2 сферические). Прямоугольная дифракционная решетка – представляет собой амплитудный транспарант с коэффициентом пропускания либо 0 либо 1. Может быть получена путем замены соs на функцию . Формирует из плоской нормально падающей волны бесконечное семейство пар плоских наклонных волн. Прямоугольная зонная пластина – формирует из плоской норм. падающей волны бесконечное семейство пар сферических волн с центрами симметр. относ. пластины.

Элементы плоской оптики

Рассм, транспарант, фокусирующий волну в вершины квадрата со стороной 2D на расстоянии z от транспаранта.

, ,

,

5.4.2. Следовательно, нужен транспарант с функцией пропускания в виде суммы этих 4-х выражений: . Он не будет полностью амплитудным. Произведем замену exp на cos.

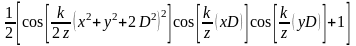(пронормировали, чтобы не превышал 1). Полученный транспарант формирует 4 сх-ся, 4 расх-ся и 1 плоскую волну.

Задача: создать транспорант, фокусирование пл. волну в бесконечно тонкое кольцо радиуса R на расстоянии z от трансп. Переходим в полярную сист корд.:

, , , . Этот элемент кольца должен создавать сфер. волну, опр. в плоскости транспаранта:

Чтобы физически реализовать транспарант, заменим exp на cos:

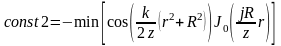
Можно построить любое заданное изображение. Такие транспаранты – элементы плоской оптики. Недостатком таких транспарантов являются побочные волны.

5.5. Дифракция некогерентного излучения: 2 //-ые щели на расст. 2a друг от друга. Угловой спектр: Интенсивность: _. Оптич. спектр равном-ый и заним. полосу: , тогда интен-сть Картина пропад. начин. с угла (2е число - период, 3е - число видим. периодов). Пусть тот же транспарант освещ-ся монохр- им светом под углом _. Падающ. волна под углом создаёт картину 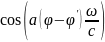, по всем углам: _. Т.о. дифр. картина исчез., IF щели транспаранта раздв. на расст. IF то предель. расст. между щелями 50 мкм. IF 6*10^-6=>8 см. Этот факт - в основе звездных интерферометров. Дифракция на взвеси частиц: Диф-ция на стохастич. наборе кругл. непересек-ся непрозр. экранах разн. диаметра. Р/м 1 непрозр. экран. Замена прозр. частей на непрозр. в целом не меняет дифракц. картины. Ф-ция транс.: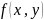 Дифр. Картина опрд.: F(v_x ,v_y), спектр заменяет с.о.:1- - F(v_x ,v_y) К видим. части спектра будет относ-ся ярк. точка (пр-п Бабинэ). Суммар. дифр. картина больш. числа кругл. непрозрачн. экранов, сдви-ых кажд. на x_n y_n, приведёт к: _. В кажд. т. картины - Σ комплекс. величин по модулю =1 Такая Σ имеет случ. фазу. Интенс-ть имеет вид: _. IF транспарант сост. из кругов разн. радиуса с распр-ем N(R), то распр-е интенсивн. измеренное: 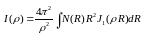Спекл-структура когерентного излучения: Р/м дифракц. когер. э.м. излуч. на стохаст. транспаранте. ··· Ф-я автокорел. явл. Фурье-образом исх. картины. Рассм-ая картина - CПЕКЛ стр-ры рассеян. излуч-я. Она возник. при рассеян. когер. излуч-ия на экране. Картина склад-ся из огром. числа точек. Эти интерф-ные картины предст. собой синусоиды. Чем > размер стохаст. транспаранта, тем < миним. период состав-щих картину синусоид. IF степ. когер-ти будет не достат. высока, то интep-ция на парах элем-ов с большими дистанциями будет с равномер. засветкой. Спекл может наблю-ся при высок. когер-ти излучения.

5.6.Линзы как Фурье-процессор. Линзы 1цу превр-ют в экспоненту: , L-фокус.расст.линзы. Разберем процесс формир. изображ. Пусть изобр-ние располож. перед линзой. В задн. плоск. получим изобр-ие. Далее это изобр-е будет распр-ся в прос-тве и на расст. z oт линзы будет иметь вид

на_расст. z=L: IF изобр-е отстоит от линзы на расст. d. В плоскости 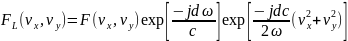Если d=L, то изобр-е в задн. фокаль. плоск. в точн. совп. со спектром изобр-я в передн. фокаль. плоск.

Пример 1:Пусть на линзу падает плоск. наклон. волна с углами , 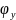. В перед. фокаль. плоск. изобр-е известно:

а изобр-е в задн. фокаль. плоск.

Пример 2: обр. задача: ;

–изобр-е соот.пл. волне.

Рассм-м процесс форм. изображ. объективом.Телескоп.В этом случ. сущест. удалён. объект, и он созд. в плоск. линзы некот. распр-е ампл-ды поля.

т.е. получили переверн. и масшт-ное изоб-ние.

Форм-ние линзой изоб-я:Пусть перед линзой на расстоянии а находится ярк. т. с координатами х0 и у0. и эта т. создает сфер. расх-ся волну. И в плоскости линзы это волна может быть представлена в виде После преобразования линзой Т.о. за линз. сф. волна сх-ся в т. с коор-ми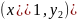 и отстоящ. от линз. на расст: . При налич. апертуры домнож. на ф-ю Тогда изоб-е Дифрaк-ые пределы объектива: р/м об-в с фокус. расст. L и круг-й апертурой R. На расст. D от плоск. создаст в плоск. линзы изобр. . Т.к. линза – ограниченная апертурой R, то надо домнож. на ф. апертуры W(x,y). В задн. фокаль. плоск. линзы будет сфор-но изобр. в виде спектра Получ.изобр. в зад. фокал. плоск. Это означ. что детали не будут разл-ся, т.е. они размоются. Это опред. угл-ю разр-ю спос-ть объектива .

5.7.Пространственная фильтрация. Св-ва линзы- уник-ые. Нет анал-ых систем, при прохожд. ч/з котор. сигнала, на вых. набл-ся его спектр. Эт св-во линзы позвол. строить класс систем, облад-их уникальными св-ми. Структура: 2 линзы располож. т.о., что их оптич. оси совп., а задн. фок. пл-ть 1й л. накл-ся на перед. фок. плоскость 2й. Мы перех. от сист. с 1й линзой к сист. с 2я линз. Будем рассм. изобр. f(x,y) в перед. фок. пл. 1й линзы. Л. это изобр. преобр. и в зад. фок. пл. Далее 2я л. преобр. это изобр. и в ее зад. фок. пл. - спектр.

Т.е. сист. перевер. исх. изобр. в зад. фок. пл. можно постав. ампл. транспарант. И тогда изобр. домнож-ся на ф. этого транс-та. и в зад. ф. пл. появ-ся уже отф-ное изобр.

Cист. явл. изопланарной. Особ-ть системы - можно легко менять имп.хар-ку. Такую с. будем назыв. простр. фильт-м (оr оптический процессор).Перед. фок. пл. системы – 1я фок. пл. 1й л., зад. фок. пл. – зад. фок. пл. 2й л. Простейш.простр. фильтры Поместим в средн. фок. пл. опт. проц. маленьк. непрозр. пятнышко на опт. оси. Т.е фильтр долж. вырез. 0ю простр. частоту- пост. составл. изобр-я. Для изобр-й, предст-х чёрн.детали малой площ., на абс. белом фоне фильтр раб. как уст-во обращ. к контрасту. IF тёмн.пятно на трансп. сделать частич.пропуск. свет, то ф. будет частич. пропуск. пост. состав-ю. И наоб., IF транспарант имеет вид кругл. прозр.пятна , то исчезнут мелк.детали изобр-я. IF менять диам. тёмн.пятна, то получ.фильтр высок.частот. IF трансп. овальный, то контр-сть по верт. и гориз. будет разным. Можно сдел. пятн. красным. То ф. будет размаз. красн. детали изобр-я. Пусть тр-ант 2мерн. решетка идеал.точек. Данный ф. мультиплиц-ет исх.изобр.

М-д Свили(оптич.неодн-ти)Прим.простр. ф, трансп. кот. предст. пласт-ку, прозр. с 1й стор. и непрозр. с другой. .

. IF все коэф-ты опустить, то преобр. фильтра: . Ф.осущест-ет преоб. Гильб. по х.

Пусть изоб. предст. прозрач. квадрат со ст-ной а. Этот квадрат даёт фаз. сдвиг φ. За пределами квадрата резуль-щее изобр. нулевое.

Особ-ти этого примера: 1)Вых. изобр. по форме не совп. со входным. 2) М-д неспособ. различ. полож. от отриц. сдвиг фаз. Метод темного поля.Суть м.- удаление пост. состав-щей. Транспарант предст.собой прозр. экран с тёмн. пятн. в ц.. Вых. изобр. предст. собой прозр. фронт и на нём есть небольшие фаз. объекты. Площ. маленькая и можно учит., что пост. состав-щая изобр.=1, после вычит. пост. состав. изобр. будет иметь вид .

Т.о. форма фазовых объектов сохр-тся. Этот м. имеет недостаток – не чувствителен к знаку.

Эти методы не способны защитить линейное фаза-амплитудное преобр-ние.