
- •5.1.1. Задачи, методы и основные подходы Фурье-оптики, плоские волны в параксиальном приближении, угловой спектр.
- •5.1.2. Плоские волны в параксиальном приближении. Угловой спектр
- •5.2. Двумерное преобразование Фурье точки, линии решетки линий, мультиплицированного отверстия.
- •5.3.1. Дифракция Френеля, дифракционные решетки, синусоидальная решетка, фазовые транспаранты.
- •5.4.1. Сферические волны, линза и зонная пластинка, элементы плоской оптики
- •5.8. Восстановление размытых изображений.
5.1.1. Задачи, методы и основные подходы Фурье-оптики, плоские волны в параксиальном приближении, угловой спектр.
О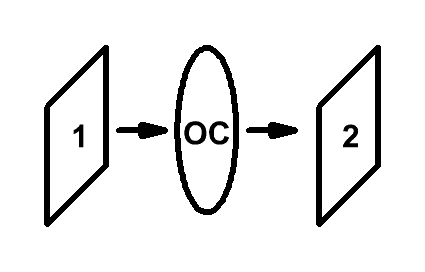 сновная
задача – обработка изображения оптической
системой (ОС). 1) Распространение ЭМИ от
1-й плоскости до ОС; 2) Преобразование в
ОС; 3) Распространение ЭМИ от ОС до 2-й
плоскости. Задачам дифракции и связанным
с ним проблемам посвящена Фурье-оптика
(ФО)..
сновная
задача – обработка изображения оптической
системой (ОС). 1) Распространение ЭМИ от
1-й плоскости до ОС; 2) Преобразование в
ОС; 3) Распространение ЭМИ от ОС до 2-й
плоскости. Задачам дифракции и связанным
с ним проблемам посвящена Фурье-оптика
(ФО)..
Распространение ЭМВ. Рассмотрим пустое пространство без свободных зарядов. Запишем ур-я Максвелла системе СГС:
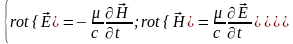 .
Отсюда
.
Отсюда
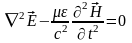 ,
,
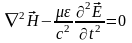 – волновые уравнения, решения ищутся
в виде:
– волновые уравнения, решения ищутся
в виде:
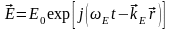 ,
,
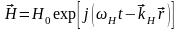 ,
,
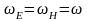 – частота;
– частота;
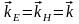 – волновой вектор.
– волновой вектор.
 .
.
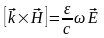 ,
,
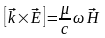 .
Получим плоскую ЭМВ
.
Получим плоскую ЭМВ
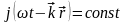 .
Любая ЭМВ является суперпозицией плоских
волн.
.
Любая ЭМВ является суперпозицией плоских
волн.
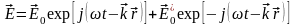 Пусть
Пусть
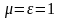 ,
рассматриваем только
,
рассматриваем только
 ,
так как
,
так как
 из
него выводится. Основные подходы,
используемые в Фурье-оптике: 1) рассм.
только линейные системы. Алгоритм:
произвольная волна -> суперпозиция
элементарных волн -> суперпозиция
реакции. 2) исп. параксиальное приближение
(углы
из
него выводится. Основные подходы,
используемые в Фурье-оптике: 1) рассм.
только линейные системы. Алгоритм:
произвольная волна -> суперпозиция
элементарных волн -> суперпозиция
реакции. 2) исп. параксиальное приближение
(углы
 ).
).
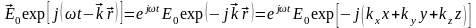
В параксиальном
приближении
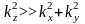 ,
,
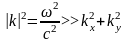 ,
,
 .
ЭМВ в параксиальном приближении:
.
ЭМВ в параксиальном приближении:
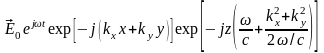 .
В качестве элементарных сигналов выберем
.
В качестве элементарных сигналов выберем
 -функции
-функции
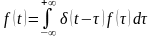 .
Так как система линейна
.
Так как система линейна
 .
.
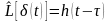 – импульсная характеристика. Инвариантность
относительно сдвига времени:
– импульсная характеристика. Инвариантность
относительно сдвига времени:
 .
.
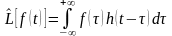 – свертка. Изображение должно выражаться
через входное изображение
– свертка. Изображение должно выражаться
через входное изображение
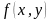 и импульсную характеристику ОС:
и импульсную характеристику ОС:
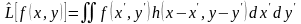 .
Это возможно при условии
.
Это возможно при условии
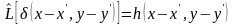 – условие изопланарности системы.
– условие изопланарности системы.
5.1.2. Плоские волны в параксиальном приближении. Угловой спектр
Рассмотрим плоскую ЭМВ, распр-ся под малым углом вдоль z.
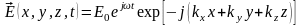 .
Направление распространения волны
можно определить через два угла
относительно оси z:
.
Направление распространения волны
можно определить через два угла
относительно оси z:
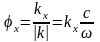 ,
,
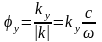 .
В плоскости z=0
эта волна будет создавать поле:
.
В плоскости z=0
эта волна будет создавать поле:
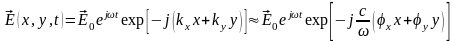
Не учитываем
зависимость от времени.
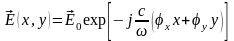 .
Запишем спектр изображения:
.
Запишем спектр изображения:
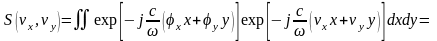
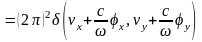 ,
те. спектр представляет собой дельта
функцию, сосредоточенную в точке с
коорд.:
,
те. спектр представляет собой дельта
функцию, сосредоточенную в точке с
коорд.:
 .
Плоская ЭМВ, направление распространения
которой определяется
.
Плоская ЭМВ, направление распространения
которой определяется
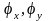 создает
в плоскости z=0
изображение, спектр которого представляет
собой дельта функцию, сосредоточенную
в точке с указанными выше координатами.
Это – основа ФО. Фурье-спектр изображения
соотв. угловому спектру создающего его
излучения. Т.о., для нахождения углового
спектра необх. и дост. Вычислить 2-хмерное
ПФ распределения амплитуды ЭМИ.
создает
в плоскости z=0
изображение, спектр которого представляет
собой дельта функцию, сосредоточенную
в точке с указанными выше координатами.
Это – основа ФО. Фурье-спектр изображения
соотв. угловому спектру создающего его
излучения. Т.о., для нахождения углового
спектра необх. и дост. Вычислить 2-хмерное
ПФ распределения амплитуды ЭМИ.
5.2. Двумерное преобразование Фурье точки, линии решетки линий, мультиплицированного отверстия.
Прямое ПФ:
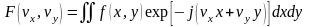
Обратное ПФ:
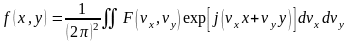
Свойства 2-хмерного ПФ:
1) Линейность прямого и обратно ПФ:
 ,
,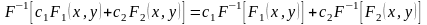
2) Сдвиг:
 :
:

3) Масштабирование
 :
:
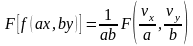
4) Свертка:

5) Произведение

Примеры двумерных ПФ. Точка, линия.
ФО двумерной ф-ции есть угловой спектр плоской нормально падающей волны, дифрагировавшей на транспаранте, соответствующим данной ф-ции.
1) Точка:
 :
:

2) Линия:
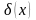 :
:
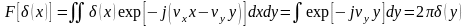
Дифракция на бесконечно тонкой вертикальной щели дает бесконечно тонкую горизонтальную линию.
3) двухмерная
решетка линий:
 .
.

4) Мультиплицированное отверстие. Задача – найти ФО мультиплицированного транспаранта, построенного математическим размножением.
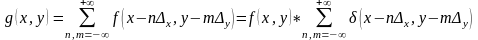
Теорема о свертке:
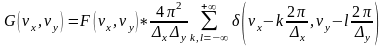 .
.
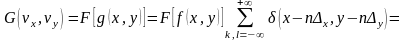
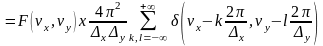
Т.е. исходный спектр оказывается промодулированным исходной решеткой точек.
