Санкт-Петербургский Государственный Политехнический Университет
Радиофизический факультет
Отчет по лабораторной работе №1
« Экспериментальное исследование численных методов решения систем линейных алгебраических уравнений »
Выполнили студенты гр. 2096/2
Проверил: Степанов E. А.
Санкт-Петербург
2012 год
Цель работы.
Изучение прямых и итерационных методов решения систем алгебраических уравнений с позиций точности получаемых решений и сходимости итерационных процессов
Сравнить между собой естественное и стандартное числа обусловленности матрицы, а также - точное значение стандартного числа обусловленности с его оценкой, вычисленной процедурой DECOMP.
(Таблица составлена для матриц порядка 8)
-
№
µ 1
µ 2
cond
1
2.305E+0002
3.310E+0002
7.913E+0001
3
2.196E+0001
4.021E+0001
2.231E+0001
4
5.560E+0000
1.796E+0001
1.318E+0001
5
1.500E+0010
1.389E+0010
2.446E+0010
6
3.679Е+0015
3.824Е+0018
8.447E+0018
7
2.654E+0012
7.096E+0013
4.816E+0013
8
7.754E+0007
1.425E+0008
9.246E+0007
10
9.881E+0008
3,462E+0009
2.581E+0009
11
1.147E+0013
2.496E+0014
5.763E+0013
12
2.487E+0014
4.882E+0016
4.102E+0016
13
1.270Е+0007
3.311Е+0007
2.879E+0007
Гистограмма для хорошо обусловленных матриц
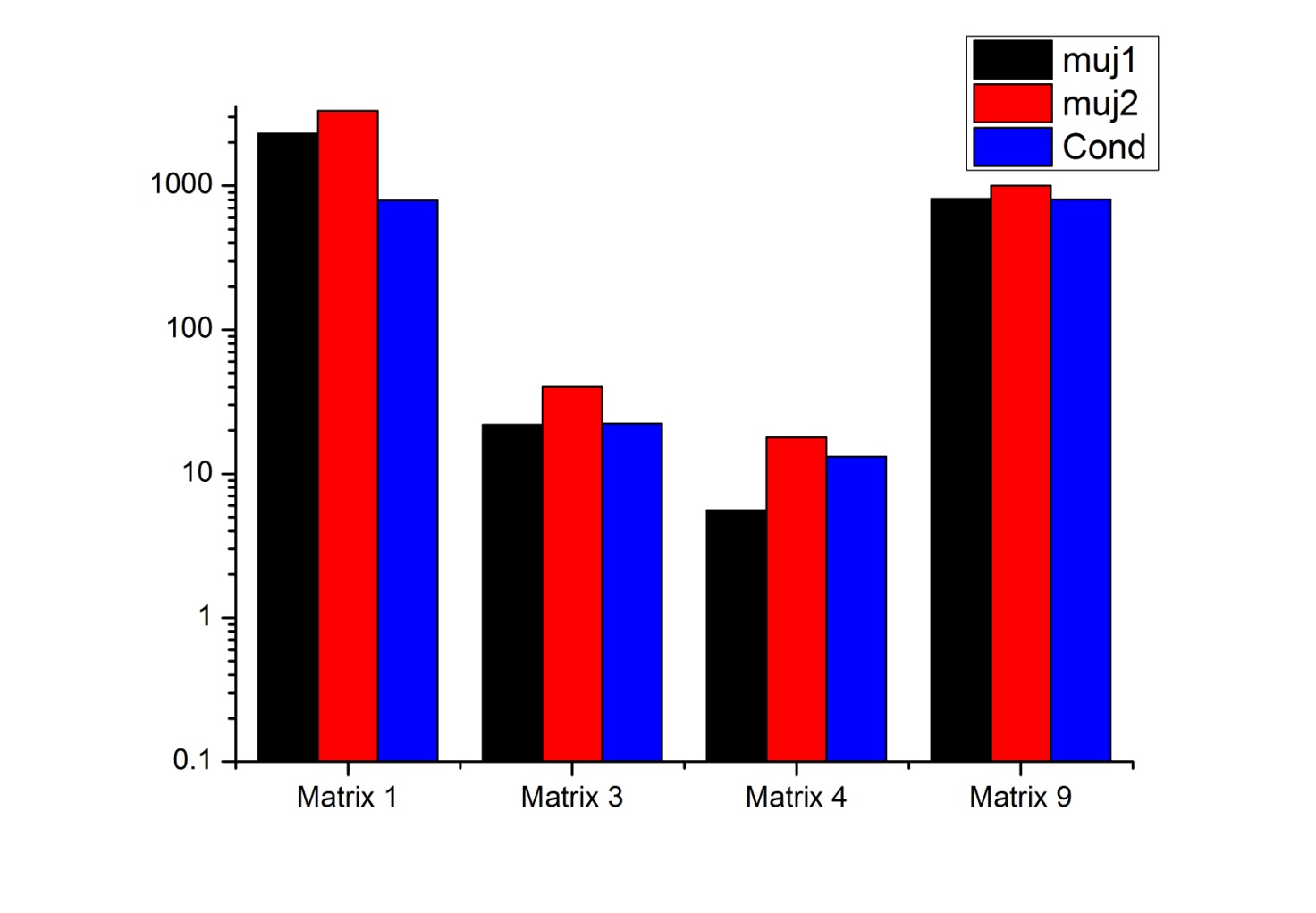
Гистограмма для плохо обусловленных матриц
Как следует из таблицы, стандартное число обусловленности (µ2) в большинстве случаев больше, чем естественное число обусловленности (µ1) или оценочное значение стандартного числа(Cond). Т.о. стандартное число обусловленности дает завышенную оценку возможной ошибки вычисления. Но так как вычисление µ1, а стало быть и возможной ошибки решения, можно сделать только после отыскания самого решения, то эффективнее использовать значение cond, отыскание которого требует малого количества дополнительных операций и дает довольно точное значение числа обусловленности.
Оценить точность решений, получаемых методом исключения Гаусса для систем с одинаково хорошо обусловленными матрицами порядка от 3 до 15; провести анализ точности, как функции порядка матрицы; сравнить фактически получаемую ошибку с ее оценками.
-
№
порядок
COND
Real Error
ErrEst(cond)
3
3
4.074E+0000
8.084E-0013
3.63E-0012
8
2.231E+0001
8.084E-0012
2.39E-0011
13
5.036E+0001
4.933E-0011
2.25E-0010
15
6.394E+0001
2.147E-0011
1.56E-0010
4
3
3.541E+0001
3.234E-0011
3.34E-0011
8
1.318E+0001
2.425E-0012
2.16E-0011
13
4.555E+0001
5.861E-0012
6.35E-0011
15
2.750E+0002
8.075E-0011
1.27E-0009
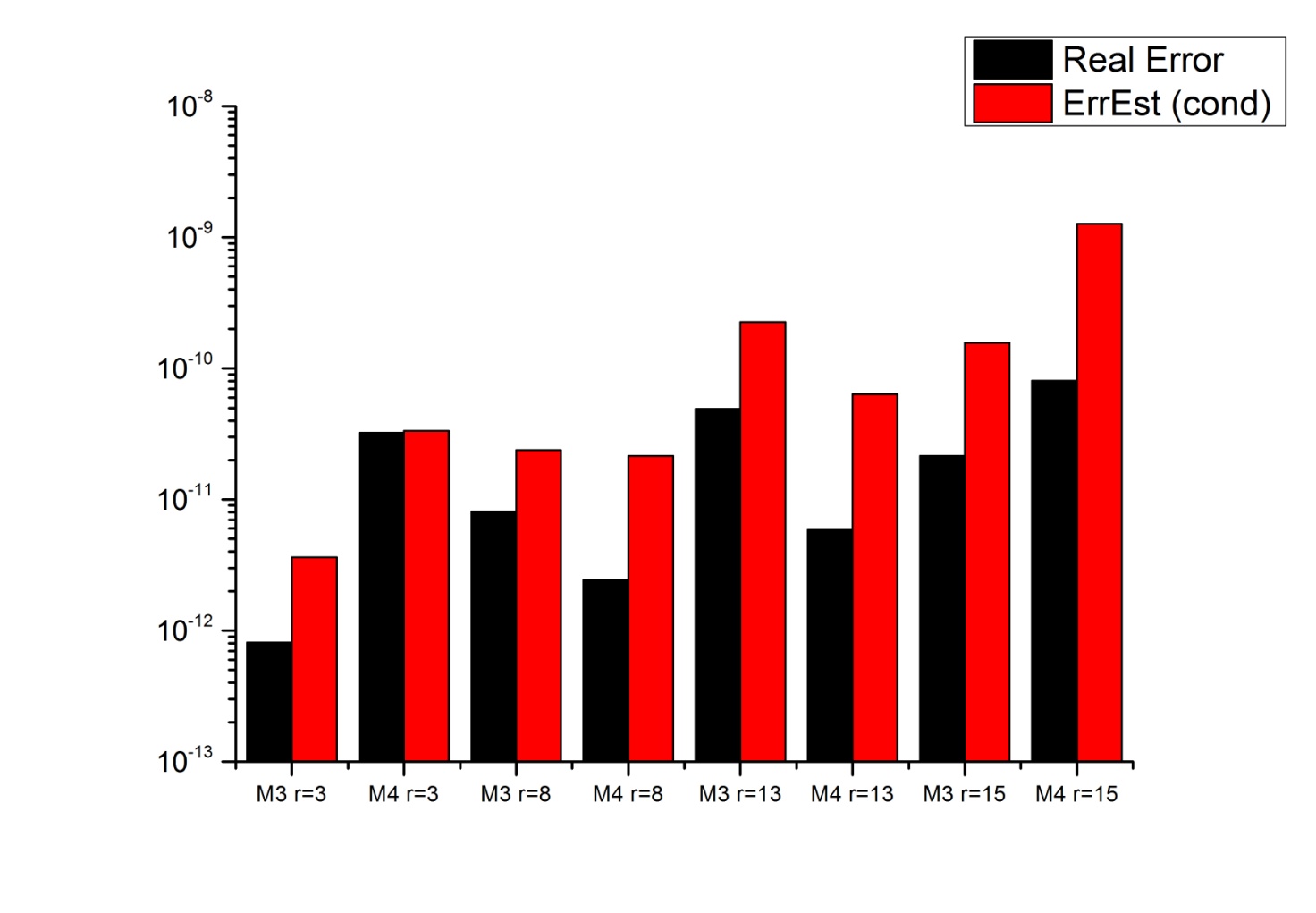
Как следует из таблицы, оценка фактической ошибки решения по числу обусловленности, полученная процедурой DECOMP, имеет несколько завышенный результат по сравнению с действительной ошибкой вычисления. Этого и следовало ожидать, исходя из способа получения этой оценки.
Использование метода исключения Гаусса дает достаточно точное решение. Однако с ростом порядка матрицы величина ошибки так же растет. Хотя в пределах рассмотренных нами порядков матрицы уменьшение точности незначительное.