30.Равномерный закон распределения. Математическое ожидание и дисперсия равномерно распределенной случайной величины.

Н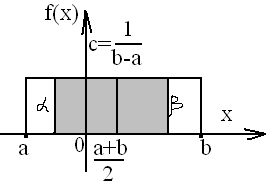 епрерывная случайная величина Х имеет равномерный закон распределения на отрезке [а, b] если ее плотность вероятности ϕ(х) постоянна на этом отрезке и равна 0 вне его, т.е. 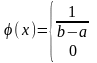при Кривая распределения ϕ(х) и график функции распределения F(х) случ величины Х приведены на рис.

Теорема: Функция распределения случайной величины Х распределенной по равномерному закону, есть 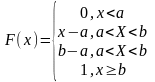. Ее математическое ожидание а дисперсия

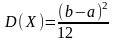
31Показательный закон распределения

О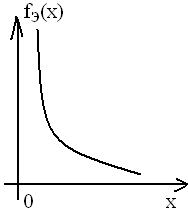 пр.3. Непрерывная случайнай величина Х имеет показательный закон распределения с параметром λ>0, если ее плотность вероятности имеет вид

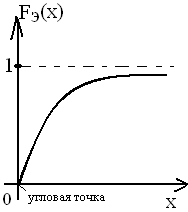
Функция распределения показательного закона: F(x) = 0 при х < 0 и F(x) = 1 – 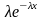при х ≥ 0.

Математическое ожидание, дисперсия и среднее квадратическое отклонение показательного распределения соответственно равны: M(X) = 1/ λ, D(X) = 1/ λ², σ(X) = 1/λ.

32 Нормальный закон распределения. Гауссова кривая, ее свойства. Математическое ожидание и дисперсия случайной величины, распределенной по нормальному закону

Непрерывная случайная величинаХ имеет нормальный закон распределения с параметрами а и σ ², если плотность вероятности имеет вид:

∙

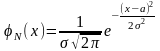
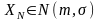
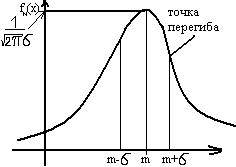
Теорема: Математическое ожидание случ.величины Х распределенной по нормальн закону, равно параметру a этого закона, т.е. M(x)=a а ее дисперсия – параметру σ ², т.е. D(x)= σ ²

Опр.2 Нормальное распределение с параметром N(0,1) наз-ся стандартным нормальным распределением.

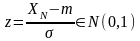; Т.о. случ-я вел-на z имеет станд. нормалное распределение

33.Функция Лапласа и ее свойства. Функция распределения случайной величины, распределенной по нормальному закону.

Функция, распределения случ величины Х , распределенной по нормальному закону, выражается через ф-ю Лапласса Ф(х) по формуле:

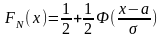
Вероятность попадания случайной величины между точками a и b для нормального распределения:

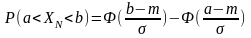
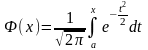— функция Лапласа

Свойства ф-ии Лапласа: 1) Ф(-х)= –Ф(х) => нечётная; 2) ; 3) 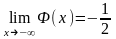; 4) x 5 => Ф(х) 1/2

34. Свойства нормально распределенной случайной величины: вероятность попадания на отрезок, отклонение от математического ожидания, правило «трех сигм».

Свойства:

1.Вероятность попадания случ велич Х, распределенной по нормальному закону в интервал [х1,х2] равна 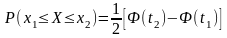где

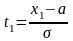
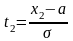
2.Вероятность того, что отклонение случайной величины Х, распределенной по нормальному закону, от мат ожидания a не привысит величину ∆>0 (по абсолютной величине) равна 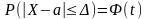где t=∆∕σ

3. правила трех сигм

Если случайная величина Х имеет нормальный закон распределения с параметрами a и σ² , то практически достоверно, что ее значения заключены в интервале (a-3 σ,a+3 σ)

35. Локальная теорема Муавра-Лапласа: Если вероятность P наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие произойдет m раз в n независ испытан при достаточно большом числе n приближенно равна P_m,n = φ(x)/ φ(x) = 1/√2π ∙ exp( –x²/2 ), x = (m – np) /

φ(x) – плотность нормального распределения.

1. Четная ф-я

2. Монотонно убыв при при положительных значениях

В случае, когда p q 0,5 рассчёты по этой ф-ле и по ф-ле Бернулли практически совпадают