26.Биномиальный закон распределения. Математическое ожидание и дисперсия случайной величины, распределенной по биномиальному закону

Дискретная случ величина Х имеет биномиальный закон распределения с параметрами n,p если она принимает значения 0,1,.. m,n с вероятностями : P(X=m) = C^m_n p^m q^n-m.

Или другими словами: при повторении n одинаковых независимых опытов некоторое событие А может случиться k раз. Если каждый раз вероятность результата А есть р, то случайная величина имеет биномиальное распределение.

Опр.3. Математическое ожидание биномиального распределения равно произведению числа испытаний на вероятность появления события в одном испытании: M(X) = np.

Опр.4. Дисперсия биномиального распределения равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании: D(X) = npq.

27.Теорема Пуассона. Формула Пуассона

Теорема Пуассона: Если число опытов n велико, а вер-ть успеха в отдельном опыте р мала (0<p<1) и произведение np= λ = const, то ф-лу Пуассона с параметром λ =.np м приблизительно применять вместо ф-лы Бернулли: P_n(m) = C^m_np^mq^n­–m причём k=0,1,…n,..

Замечание: использование ф-лы Пуассона как предельной для ф-лы Бернулли оправдывает себя при npq 9

Теорема в кремере: Если вероятность P наступления события А в каждом испытании стремится к 0 при неограниченном увеличении числа n испытаний, причем произведение np стремится к постоянному числу λ то вероятность P_m,n того, что событие А появится m раз в n независимых испытаниях, удовлетворяет предельному равенству

Из этого предельного равенства вытекает приближенная формула Пуасона

28.Закон распределения Пуассона. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона.

Дискретная случ величина Х имеет закон распределения Пуассона м параметром λ>0? Если она принимает значения 0,1,2,..m.. с вероятностями P(X=m) = λ^m e^-λ / m!, где m – число появлений события в n независимых испытаниях, λ = np (среднее число появлений события в n испытаниях),

Опр.6. Математическое ожидание распределения Пуассона равно произведению числа испытаний на вероятность появления события в одном испытании: M(X) = np = λ.

Опр.7. Дисперсия распределения Пуассона равна произведению числа испытаний на вероятность появления события в одном испытании, то есть равна математическому ожиданию: D(X) = np = λ.

29.Геометрическое распределение. Гипергеометрическое распределение.

Дискретная случайная величина Х=m имеет геометрическое распределение с парам P , если она принимает значения 1, 2,...m.. с вероятностями , где 0 < р < 1, q= р - 1

Случ величина X=m имеющая геометрич распределение, представляет собой число m испытаний, проведенных по схеме Бернулли, с вероятностью p наступления события в каждом испытании до первого положительного исхода.

Мат ожидание случ величины Х имеющей геометр распределение с парам P

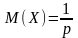
А дисперсия .

Гипергеометрическое распределение

Дискретная случайная величина Х имеет гипергеометр распределение с параметрами n,M,N если она принимает значения 0,1,2, m,…min (n,M) с вероятностями , где M<=N, n<=N; n,M,N – натуральные числа

Мат ожидание случайной величины Х имеющей гипергеометрическое распределение с параметрами n,M,N есть а ее дисперсия

Гипергеометрическое распределение можно рассматривать как модификацию биномиального распределения для случая конечной совокупности, состоящей из N объектов,M из которых обладают этим свойством. Можно сказать что при N функция вероятнос тей гипергеом распределения стремится к соответствующей функции биномиального закона.