55.Общая схема проверки гипотез:

1. выдвигается основная гипотеза Н₀ и альтернативная Н_1; выбирается α

2. выбирается статистика К, с помощью кот-ой будет проверяться выдвинутая гипотеза

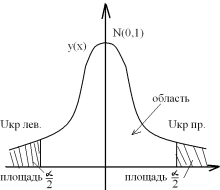
3. Вся область возможных значений статистики к разбивается на 2 непересекающиеся области: критическую и область принятия гипотезы, разделённые критическими точками

4. По имеющейся выборке выч-ся значение статистики К_набл и определяют, в какую из 2-х областей оно попадает, и на основании этого принимается решение относит-но истинности Н₀

Критическими точками (границами) k_кр называют точки, отделяющие критическую область от области принятия гипотезы.

Правосторонней называют критическую область, определяемую неравенством К > k_кр, где k_кр – положительное число.

Левосторонней называют критическую область, определяемую неравенством К < k_кр, где k_кр – отрицательное число.

Двусторонней называют критическую область, определяемую неравенством К < k₁, K > k₂, где k₂ > k₁.

В частности, если критические точки симметричны относительно нуля, то двусторонняя критическая область определяется область определяется неравенствами (в предположении, что k_кр > 0) К < – k_кр, K > k_кр, или равносильным неравенством: | K | > k_кр.

Опр. Область допустимых значений – совокуп-ть значений критерия К, на основании кот-ых принимается основная гипотеза. К–случ.вел-на

57-58. гипотезы о мат. ожидании нормальной генеральной совок-ти

А) Дисперсия генер. совок-ти известна

Н₀: m=a, a=const

H₀: M[ ]=a

Значимо ли различие между выборочной средней и генеральной средней – U-статистика, кот-я имеет стандартное нормальное распределение. N(0,1)

1. Н ₁: m a – двусторонняя критич. обл.

2. Н₁: m>a – правостор.

3. Н₁: m<a – левосторон.

Для 1): Из таблицы наход-м правую крит. точку, а т.к. распредел. Симметрично, то k_{кр лев} = k_{кр пр}. Если |U_набл| < U_кр., то нулевую гипотезу не отвергаем.

Для 2): Если U_набл < U_кр., то нет оснований отвергать основную гипотезу. U_{кр лев} = –U_{кр пр}

Для 3): U_набл < U_кр Н₀ отвергаем U_{кр лев} = –U_{кр пр}

Б) Дисперсия неизвестна

Н₀: m=a

Cтатистика Т имеет распределение Стьюдента со k = n–1 степенями (n-объём выборки)

Н₁: m a – двусторонняя критич. обл. По таблице находим t_дв.кр=t( ;k)

Стьюдент стремится к N;

Н₁: m<a – левосторон. критич.обл. Ищем t_кр.пр =t( ;k) затем t_дв.кр= –t_{кр. пр}

Сравнение генеральной дисперсии с выборочной дисперсией.

N=30,50 .

Если то .

Н₀: ,

Н₀:

Дисперсия – рассеяние значения контролируемого параметра. Разбросы любых измерений – это дисперсия.

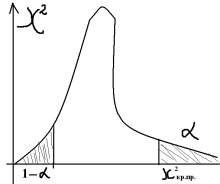, где k=n–1

Если правосторонняя критическая область, то Крит. точка находится по таблице крит-их точек «хи квадрат» распределения

Для левостор. Обл.:

Для двустроронней: , .

Н₁: