49. Метод наибольшего правдоподобия
Случай непрерывных распределений
Пусть x , x … x – независимая выборка из непрерывного распределения с плотностью p(x; θ).
Определение 1: Функция вида L(x , x … x ; θ)=p(x ; θ)…p(x ; θ) называется функцией правдоподобия.
Определение
2: Оценкой наибольшего правдоподобия
параметра θ называют число
,
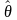которое находится из условия L(x
,
x
…
x
;
)=max
L(x
,
x
…
x
;
θ)
При
выполнении некоторых условий, смысл
которых состоит в том, что p(x;
θ) – достаточно гладкая функция, а
интеграл
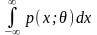=1
достаточно быстро сходится, оценка
максимального правдоподобия обладает
следующими свойствами:
она состоятельна
она асимптотически нормальна, т.е при больших n можно рпиближенно считать, распределение приближенно нормельным.
она асимптотически эффективна, т.е при больших n оценку можно считать близкой к эффективной.
Недостатком метода является то, что иногда оценки получаются смещенными.
Случай дискретного распределения
Определение
1: Пусть P(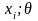
)=P
,
где
–
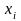число из выборки, а
– та случайная величина, которая приняла
значение
.
Функция вида L(x
,
x
…
x
;
θ)=P(x
;
θ)…P(x
;
θ) называется функцией правдоподобия
в дискретном случае.
Оценкой наибольшего правдоподобия параметра θ называют число , которое находится из условия L(x , x … x ; )=max L(x , x … x ; θ).
Пример:
Методом наибольшего правдоподобия
найти оценку параметра λ распределения
Пуассона P
=
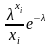, λ>0,
–
целые неотрицательные числа.
Решение.
Составляем функцию правдоподобия L(x
,
x
…
x
;
λ)=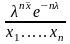
И
находим, что ее максимум достигается
в точке
=
.
52 .Интервальной называют оценку, которая определяется двумя числами – концами интервала, покрывающего оцениваемый параметр.
Доверительным называют интервал, который с заданной надёжностью γ покрывает заданный параметр.
Интервальной оценкой (с надёжностью γ) математического ожидания а нормального распределённого количественного признака по выборочной средней хв
1. при известном среднем квадратическом отклонении σ генеральной совокупности служит доверительный интервал хв – t (σ/√n) < a < хв + t (σ/√n), где δ = t (σ/√n) – точность оценки, n – объём выборки, t – значение аргумента функции Лапласа Ф(t), при котором Ф(t) = γ/2.
2. при неизвестном σ (и объёме выборки n < 30) хв – tγ (s/√n) < a < хв + tγ (s/√n), где s – исправленное выборочное среднее квадратическое отклонение, tγ находят по таблицам распределения Стьюдента по заданным n (число степеней свободы k = n – 1) и γ.
Интервальной оценкой (с надёжностью γ) среднего квадратического отклонения σ нормально распределённого количественного признака Х по исправленному выборочному среднему квадратическому отклонению s служит доверительный интервал s (1 – q) < σ < s (1 + q) (при q < 1), 0 < σ < s (1 + q) (при q > 1), где q находят по таблицам распределения χ2 по заданным n и γ.