1.Комбинаторика
Правило суммы: Если некотор объект А может быть выбран m спос, а B-k способами,(не такими как А), то объект либо А либо В может быть выбран m+k=n способами.
Правило произведения: Если объект А мб выбран m способ, и после каждого такого выбора другой об. В м. выбрать k способами, независимо от выб. Об. А, то пару «А и В» в указанном порядке можно выбрать m*k способами
Совокупность сост из m различных элементов а1,а2,.. an – генеральная совокупность без повторений.
Некоторое подмножество, сост из m элементов (M<=m) генер совокупности без повторений наз. Выборкой объемом M без повторений
Одна выборка об. Может отлич от другой выборки такого же об.:
1.хотя бы 1 элементом (составом)
2.порядком следования (порядком)
Размещен.
без повторений
из n
элементов по m
, называются такие выборки V
M
составлен из n
различных элементов генер совокупности
без повторений которые одна от другой
отличаются либо составом либо порядком
следовании элементов
Перестановки
без повторений:
назыв размещен без повторений из n
элементов по m
которое одно от др отлич порядком
следования элементов
Сочетанием без повторений из n элементов по m назыв. Такие размещ без повторений из n элементов по M котор одно от другого отлич хотя бы 1 элементом.
m!- число перестановок выбр. Элем
2. Выборки с повторениями
Генер. Совокупность с повторениями n размещений классов повтор. Элементов, причем элементы внитри одного класса счит. Одинак, а их количество неограниченно.
Подмножестьво, состоящ из m элем генеральн совокупности с повтор. – выборка об. M (с повтор)
Выборки об. M могут отлич составом, порядком.
Размещения
с повторениями
из n
элементов по M
называютчя такие выборки M,
составленные из элементов n
различных классов генер совокупн с
повторен, которые одна от другой отлич.
Лтбо составом, либо порядком следования
элементов.
Число
перестановок
n
– элементов, в котором есть одинаковые
элементы, а именно элементов i
–того типа
(i=1,2,3,k
) вычисляется по формуле
Сочетанием с повторение из элементов n класса по m называется такое размещение с повторением которое одно от другого отличается хотя бы 1 элементом
Число
сочетаний с повторениями
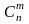
3. Классификация событий. Элементарные события. Классическое определение вероятности.
Достоверные-обязательно произойдет при реализации данного комплекса условий Ω
Невозможное – заведомо не произойдет при реализации данного комплекса условий
Случайное-может произойти а может и не произойти при реализации данного комплекса условий
Реализация данного комплекса услуг- произведено испытание
События – результаты испытаний
Несколько событий назыв несовм если появление 1 из них исключает появление другого в данном испытании
Если несколько событий несовместны, то никакие 2 не могут произойти одновременно по парной несовм.
Несколько событий назыв единственно возможн, если в результате испытания должно произойти хотя бы 1 из этих событий
Несколько событий образуют полную группу если они: 1.единственно возможны, 2.попарно несовместны
Замечание:если события, образ. Полную группу, то в результате испытания обязательно происходит только одно из этих событий
Два события образующих полную группу называются противоположными
Два события назыв противоположными если: 1. Несовместны 2. В результате испытаний обязательно произойдет одно из этих событий
Равновозможные события – ни одно из этих событий не явл более возможным чем остальные
Каждый возможный исход испытания назыв элементарн событием.Эл.события-равновозможны, образуют полную группу.
Классическое определение вероятности: вероятностью события А называпется отношение числа m эдемент событий, благоприятствующих событию А, к полному числу n всех элементов равнозначн событий образующих полную группу P(A) = m / n
4. Относительной частотой W(A) называется отношение числа m испытаний в которых событие А наступило к полному числу n фактически проведенных испытаний
W(A) = m/n, где m — число испытаний, в которых событие А наступило, а n — общее число произведенных испытаний.
Статистической
вероятностью события А называется
если число испытаний п достаточно
большое.