14.6. Методы рунге-кутты произвольного и четвертого порядков

Любой метод из семейства методов Рунге-Кутты второго порядка (14.30) реализуют по следующей схеме. На каждом ша­ге, т.е. при каждом i = 0,1, 2,..., вычисляют значения функции

а затем находят шаговую поправку

прибавление которой к результату предыдущего шага дает приближенное значение решения у(х) в точке x_i+1 = х_i + h:

y_i+1=y_i+∆y_i.

Метод такой структуры называют двухэтапным по количеству вычислений значений функции — правой части уравнения (14.1)— на oдном шаге.

Анализ устройства методов Рунге-Кутты второго порядка позволяет представить, в какой форме следует конструировать явный метод Рунге-Кутты произвольного порядка. По аналогии с предыдущим для семейства методов Рунге-Кутты p-го порядка используется запись, состоящая из следующей совокупности формул:

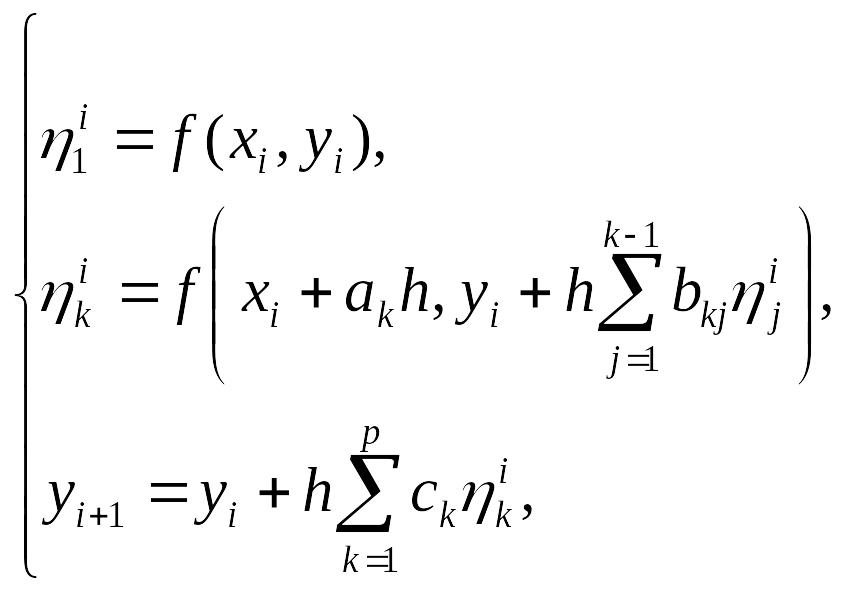(14.32)

где k = 2,3,..., p (для p-этапного метода). Многочисленные параметры c_k, a_k, b_kj,фигурирующие в формулах (14.32), подбираются так, чтобы получаемое методом (14.32) значение y_i+1 совпадало со значением разложения y(x_i+1) по формуле Тейлора с погрешностью O(h ^p+1 ) (без учета погрешностей, совершаемых на предыдущих шагах).

Наиболее употребительным частным случаем семейства методов (14.32) является следующий метод Рунге-Кутты четвертого порядка, относящийся к четырехэтапным и

имеющий вид:

(14.33)

He пытаясь воспроизвести выкладки, приводящие от общей записи семейства (14.32) при p = 4 к конкретному методу (14.33), дадим геометрическое толкование последнего.

Обратив внимание на то, что шаговая поправка ∆y_i есть средневзвешенная величина поправок , , , каждого этапа (с весовыми коэффициентами 1/6, 2/6, 2/6, 1/6 соответственно), проанализируем, как получаются эти поправки этапов. На первом этапе создается приращение = hf(x_i, y_i)(= hy'(x_i)), соответствующее шаговой поправке Эйлера, — это очевидно. На рис 14.2 ему отвечает отрезок ВС вертикали х = х_i+1 (точка В получена ортогональным проектированием точки А на эту вертикаль).

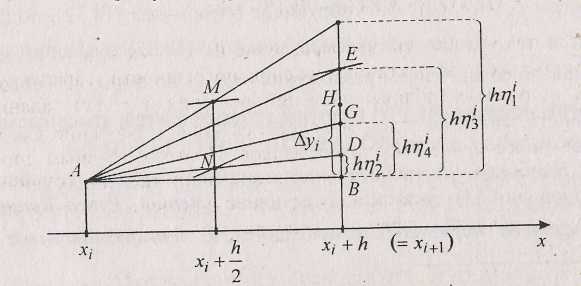
Рис. 14.2. Геометрическая иллюстрация одного шага метода Рунге-Кутты четвертого порядка

Так как точка М, благодаря свойству средней линии треугольника (см. ∆АВС), имеет ординату y_i+ , то определяет

значение f(M), служащее (согласно связи у' = f(x, у) и геометрическому смыслу производной) тангенсом угла А в новом треугольнике с противолежащим этому углу катетом = BD. Далее, аналогично, подсчитав f(N) = f(x_i + , y_i + ) = на

вертикали х = x_i+1 откладываем следующую промежуточную (этапную) поправку = BE. Вычислив величину f(E) = f(X_i + h, у_i + ), являющуюся значением тангенса угла А во вновь получаемом ∆ABG, имеем поправку = BG последнего этапа. Итоговая шаговая поправка ∆y_i=BH есть продукт усреднения с указанными коэффициентами четырех этапных поправок — длин отрезков ВС, BD, BE и BG. Точка Н будет стартовой для следующего, i+1-го, шага метода (14.33).

Заметим, что если первый этап, как уже упоминалось, соответствует применению явного метода Эйлера, то четвертый — неявного, а второй и третий — уточненного методов Эйлера. Последний имеет более высокий порядок точности, отсюда и больший вес отвечающих ему значений этапных поправок

ЭКАЗАМЕНАЦИОННЫЙ БИЛЕТ № 9

1. Задача визуализации данных. Методы визуализации. Проекция Саммона.

Визуализация данных имеет целью дать по возможности наглядное представление исследуемых данных. Наглядность представления имеет большое значения для построения гипотез о структуре данных. Кроме того, визуализация помогает поиску зависимостей между данными. В качестве примера рассмотрим проекцию Сэммона - отображение данных на плоскость, применяемую для построение плоского отображения многомерных таблиц на экран дисплей. Все подобные методы пытаются минимизировать некоторую функцию потерь, характеризующую величину рассогласования расстояний между первоначальными и полученными векторами в пространстве малой размерности. В случае, если функцию потерь задают в виде

(здесь - расстояние между объектами i и j, соответственно, в многомерном и двумерном пространстве, N - количество объектов), ее называют ошибкой Сэммона, а соответствующий метод снижения размерности называют методом двумерного отображения Сэммона.

Реализация алгоритма начинается со случайного размещения точек-проекций на плоскость и состоит в минимизации ошибки как функции координат

.

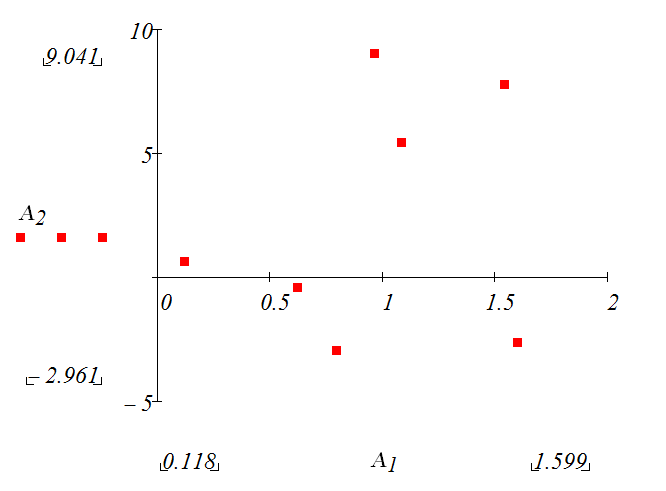
Пусть имеется «многомерная» таблица:

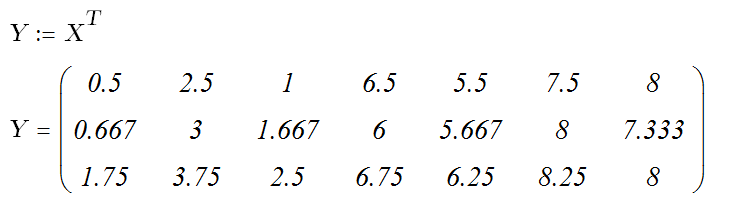
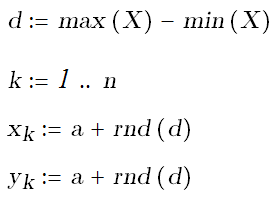
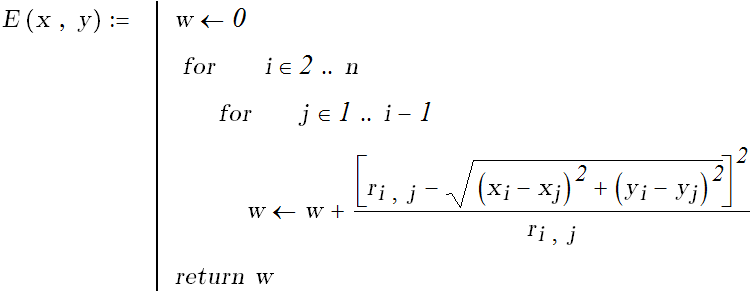
Получаем координаты точек проекций.

2. Объединения мнений на основе теории Демстера-Шафера.

Первая игра — подбрасывание монеты, где ставки делаются на то, выпадет орел или решка. Теперь представим вторую игру, в которой ставки принимаются на исход боя между лучшим в мире боксером и лучшим в мире борцом. Предположим, мы несведущи в боевых искусствах, и нам весьма трудно определиться на кого ставить.

Многие люди будут менее уверены в ситуации второй игры, в которой вероятности неизвестны, чем в первой игре, где легко увидеть, что вероятность каждого исхода равна половине. В случае второй игры, Байесовская теория присвоит каждому исходу половинную вероятность, вне зависимости от информации, делающей один из исходов более вероятным, чем другой. Теория Демпстера-Шафера позволяет определить степень уверенности, которую имеет игрок, относительно вероятностей присвоенных различным исходам

Пусть   — универсальное множество, набор всех рассматриваемых утверждений. Показательное множество,  , совокупность всех подмножеств множества  , включая пустое множество,  . Например, если:

то

По определению, масса пустого множества — ноль:

Массы оставшихся элементов показательного множества нормированы на единичную сумму:

Масса   элемента показательного множества,  , выражает соотношение всех уместных и доступных свидетельств, которые поддерживают утверждение, что определенный элемент   принадлежит   но не принадлежит ни одному подмножетсву  . Величина   относится только к множеству   и не создает никаких дополнительных утверждений о других подмножествах  , каждое из которых, по определению, имеет свою собственную массу.

Исходя из приписаных масс, могут быть определены верхняя и нижняя границы интервала возможностей. Этот интервал содержит точную величину вероятности рассматриваемого подмножетсва (в классическом смысле), и ограничена двумя неаддитивными непрерывными мерами, называеыми доверие (belief) (or поддержка (support)) and правдоподобие(plausibility):

Доверие   к множеству   определяется как сумма всех масс собственных подмножеств рассматривеаемого множества:

Правдоподобие   — это сумма масс всех множеств   пересекающихся с рассматриваемым множеством  :

Эти две меры соотносятся между собой следующим образом:

Из вышенаписанного следует, что достаточно знать хотя бы одну из мер (массу, доверие или правдоподобие), чтобы вычислить оставшиеся две. Рассмотрим проблему объединения двух независимых множеств приписанных масс. Исходное правило объединения известное как Dempster's rule of combination является обобщением Bayes' rule. Это правило придает особое значение согласию между многочисленными источниками и игнорирует все конфликтующие свидетельства с помощью нормализации. Правомерность использования этого правила подвергается серьёзным сомнениям в случае значительных несоответствий между источниками информации.

Собственно, объединение (называемое присоединенная маса) вычисляется из двух множеств масс   и   следующим образом:

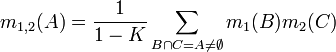
где:

 является мерой конфликта между двумя наборами масс. Нормализирующий множитель,  , соответствует полному игнорированию несоответствий и приписыванию любой массе, соответствующей конфликту, пустого множества. Следовательно, эта операция приводит к контринтуитивным результатам в случае значительного конфликта при определенных обстоятельства

ЭКАЗАМЕНАЦИОННЫЙ БИЛЕТ № 10

1. Модель бинарного классификатора объектов на основе логистической регрессии

Понятие регрессии (линейной, нелинейной в частности полиномиальной) применяется для изучения связи между случайными величинами. Практически чаще всего ограничиваются изучением изменения средних характеристик одной величины при изменении другой. Вероятностная трактовка проблемы основывается на предположении о том, что системы рассматриваемых случайных величин имеет совместное распределение вероятностей. Например, в случае двух величин X и Y , фиксируя значение одной из них, можно получить закон условного распределения другой. Если совместное распределение (X;Y) задано таблицей вероятностей pij = P(X=xi & Y=yj) , где i = 1..n ; j= 1..m , то

(4.2.1)

где

Формула (4.2.1) определяет условное распределение вероятностей случайной величины Y при условии, что X = xi. В случае непрерывного распределения с плотностями вероятностями определение условного распределения аналогично. Если ставится задача определить только числовые характеристики условного распределения вероятностей Y при условии X = x, то часто выбирается центр этого распределения или условное математическое ожидание величины Y при условии X = x.

(4.2.2)

Условное математическое ожидание есть функция от x . Эта функция называется регрессией величины Y на X (функция регрессии)

(4.2.3)

Уравнение y= f(x) называется уравнением регрессии, а график функции регрессии – линией регрессии. Линия регрессии показывает, как в среднем меняется величина Y при изменении X.

Если f(x) есть функция регрессии Y на X, то математическое ожидание квадрата отклонения величины Y от f(X) меньше, чем для любой другой функции. Это основное свойство регрессии случайной величины Y на величину X может быть принято за определение регрессии. Если функция f(x) линейна то есть f(x) = ax+b, то говорят о существовании линейной корреляции между X и Y

В случае линейной корреляции функция регрессии принимает вид

(4.2.4)

Здесь - центральный момент совместного распределения X и Y, - дисперсия X, , .

Безразмерный коэффициент - называется коэффициентом корреляции.

Для оценки параметров уравнения линейной регрессии и коэффициента корреляции проводится ряд испытаний, исходом которых являются пары , по которым вычисляются выборочные средние и дисперсии.

В качестве несмещенной оценки корреляционного момента обычно принимают эмпирический корреляционный момент

Заменяя в уравнении регрессии (4.2.4) теоретические моменты на эмпирические, получаем уравнение выборочной прямой регрессии.

(4.2.5)

где r – выборочный коэффициент корреляции

Доказывается, что эмпирическое уравнение регрессии (4.1.5) является прямой наилучшего среднеквадратичного приближения в том смысле, сумма квадратов отклонений эмпирических значений от выборочной прямой регрессии (4.1.5) меньше, чем сумма квадратов отклонений их от любой другой прямой. На этом свойстве основывается метод поиска параметра линии регрессии. Выбирается тот набор, который обеспечивает минимум суммы квадратов отклонений от искомой прямой.

На том же принципе основывается подбор кривой наилучшего приближения в случае нелинейной зависимости. Однако понятие коэффициента корреляции имеет смысл только для линейно зависимых случайных величин. Например, для экспериментально полученных значений выражающих некоторую неизвестную зависимость между переменными в предположении, что связь выражается функцией

(4.2.6)

параметр a можно получить, находя минимум функции

которая является суммой квадратов отклонений эмпирических значений от кривой регрессии (4.2.6)

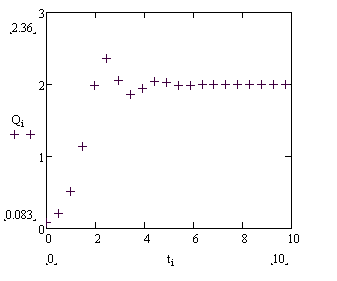
Рис. 4.1.1 Эмпирические данные по процессу установления.

Но в данном параграфе, посвященном логистической регрессии, речь идет о другой задаче. В случае логистической регрессии зависимая величина является бинарной, то есть принимающей два дискретных значения (0 – 1 ), которые часто интерпретируются как значения переменной булевского типа. Данная величина обычно отражает принадлежность некоторого объекта к одному из двух классов. И ставится задача построения регрессии с количественными объясняющими переменными и бинарной объясняемой переменной (переменной отклика). Если получить уравнение такой регрессии, то оно может служить для распознавания или классификации объектов. Поэтому в данной задаче на первом плане классификация, а построение регрессии как вспомогательный сюжет.

Данная задача является типичной задачей машинного обучения (Machine Learning): имеется выборка с объектами, распределенными по классам, на основании этой выборки строится классификатор, определяющий класс (тип, метку) объектов. Задача решается как задача нелинейной регрессии с функцией

(4.2.7)

Поскольку зависимая величина – бинарная величина, то функция (4.2.7) трактуется как вероятность того, зависимая величина примет соответствующее значение 1 (истина). Для другого значения 0 (ложь) предназначается (1 - P(x) ). Коэффициенты регрессии подбираются таким образом, чтобы обеспечить максимальное соответствие предсказания по формуле и наблюдаемыми характеристиками объектов обучающей выборки.

Использование логистической функции обеспечивает нахождение вероятности в пределах отрезка [0;1].

Подбор коэффициентов (вектор b) опирается на принцип максимального правдоподобия.

Правдоподобием называется произведение плотность совместного распределения значений Y. Для рассматриваемого случае правдоподобие записывается как произведение:

Максимум функции правдоподобия дает b. Поиск максимума переформулируем как поиск максимума логарифма от функции правдоподобия.

(4.1.8)

Если true кодируется как 1, а false как 0 , то формулу (8) можно упростить и сделать более удобной для вычислений

(4.2.9)

Значения Y равные нулю обратят в нуль первое слагаемое, равные единице второе. Полученная формула позволяет найти b в процессе максимизации выражения (4.2.9).

В качестве примера рассмотрим задачу построения классификатора для определения надежности физических лиц как заемщиков банка.

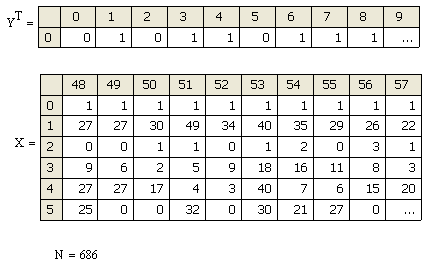
Рис. 4.2.2 Фрагмент данных по заемщикам (X) и результат их аттестации экспертами (Y).

Для выполнения программы на MathCad удобно представить таблицу данных так, чтобы данные об одном объекте располагались как вектор, и дописать к нему в качестве нулевого элемента единицу. Меточную переменную Y лучше расположить как вектор. Тогда в полном соответствии с формулой (4.2.9) записываем программу, реализующую метод максимизации правдоподобия.

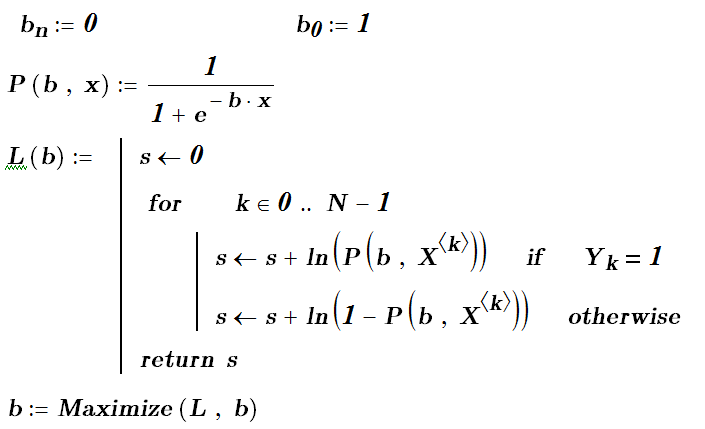
Отметим, что если мы используем инструментальную среду Deductor, то мастер «Логистической регрессии» подсчитает и отобразит вероятности значений классов (меток). Для превращения вероятностей в значение класса задаем параметр – границу вероятности (например, 0.5), отделяющую объекты одного класса от другого.

Окончательный выбор этой границы осуществляется решением оптимизационной задачи с двумя критериями, что составляет проблематику так называемого ROC- анализа. ROC (Receiver Operator Characteristic) – анализ показывает зависимость количества верно классифицированных положительных примеров от количества неверно классифицированных отрицательных примеров. В терминологии ROC-анализа первые называются истинно положительным, вторые – ложно отрицательным множеством. При этом предполагается, что у классификатора имеется некоторый параметр (в нашем случае – это параметр p), варьируя который, мы будем получать то или иное разбиение на два класса. Этот параметр часто называют порогом, или точкой отсечения (cut-off value). В зависимости от него будут получаться различные величины ошибок I и II рода. В логистической регрессии порог отсечения изменяется от 0 до 1 – это и есть расчетное значение границы для уравнения регрессии. Иногда его называют рейтингом.

Для понимания сути ошибок I и II рода рассмотрим таблицу (Таблица 4.2.1) сопряженности, которая строится на основе результатов классификации моделью и фактической (взятой из обучающей выборки) принадлежностью примеров к классам.

	Результат в обучающей выборке
Модельный результат	Положительный	Отрицательный
Классифицирован как положительный	TP	FP
Классифицирован как отрицательный	FN	TN

Таблица 4.2.1. Таблица сопряженности для расчета рейтинга.

В таблице 4.2.1 используются обозначения:

TP (True Positives) – верно классифицированные положительные примеры (так называемые истинно положительные случаи);

TN (True Negatives) – верно классифицированные отрицательные примеры (истинно отрицательные случаи);

FN (False Negatives) – положительные примеры, классифицированные как отрицательные (ошибка I рода). Это так называемый "ложный пропуск" – когда интересующее нас событие ошибочно не обнаруживается (ложно отрицательные примеры);

FP (False Positives) – отрицательные примеры, классифицированные как положительные (ошибка II рода); Это ложное обнаружение, так как при отсутствии события ошибочно выносится решение о его присутствии (ложно положительные случаи).

Что является положительным событием, а что – отрицательным, зависит от конкретной задачи. В нашей задаче благонадежность заемщика мы считаем положительным (true = 1), а отрицательным противоположное. При анализе чаще оперируют не абсолютными показателями, а относительными – долями, выраженными в процентах: Доля истинно положительных примеров (True Positives Rate):

Доля ложно положительных примеров (False Positives Rate):

Следующие две характеристики фигурируют в задаче многокритериальной оптимизации - чувствительность и специфичность модели. Собственно они служат критериями для оценки построенного бинарного классификатора.

Чувствительность (Sensitivity) – это и есть доля истинно положительных случаев:

Специфичность (Specificity) – доля истинно отрицательных случаев, которые были правильно идентифицированы моделью:

Модель с высокой чувствительностью часто обнаруживает положительные примеры даже тогда когда их нет, зато не пропускает никого из благонадежных. Наоборот, модель с высокой специфичностью чаще отсеивает как отрицательные результаты те исходы, которые следовало бы считать возможно положительными, зато диагностирует только истинно благонадежных заемщиков. В нашем примере после определения параметров логистической регрессии должен следовать расчет вероятностей примеров из выборки (Zk) и в соответствии с порогом отсечения (p) модельное значение – полученное классификатором (z)

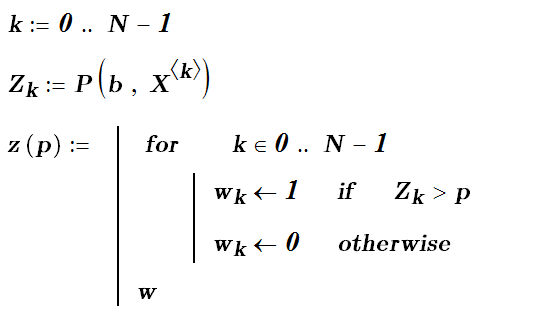
2. ROC - анализ.

Далее строится ROC-кривая. Для каждого значения порога отсечения (оно меняется от 0 до 1 с выбранным шагом h, в нашем примере h= 0.01 ) .Рассчитываются значения чувствительности Se и специфичности Sp. В качестве альтернативы порогом может являться каждое последующее значение примера в выборке. Строится график в координатах (Se;Sp) (также принято строить график в координатах (Se ;1-Sp), то есть (TPR;FPR)). В приведенной программе специфичностью названа FPR.В результате вырисовывается кривая (рис. 4.1.3), получившая название ROC-кривой.

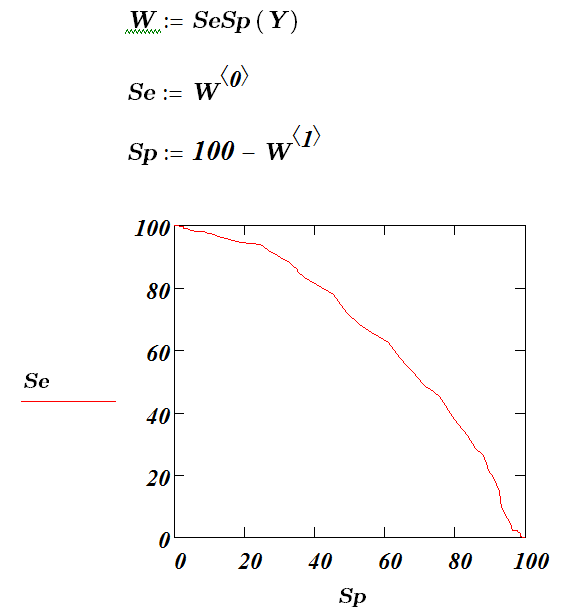
Рис. 4.2.3 ROC - кривая

Строится график зависимости: по оси Y откладывается чувствительность Se, по оси X – 100%–Sp (сто процентов минус специфичность), или, что то же самое, FPR – доля ложно положительных случаев.

В качестве порога теперь можно выбрать точку наименее удаленную от идеальной точки (0,100), которая соответствует максимальной чувствительности и специфичности.

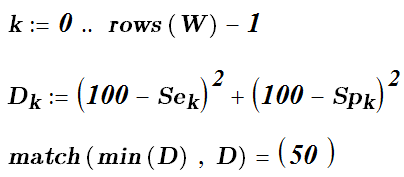
Этой точки на ROC- кривой соответствует рейтинг (точка отсечения, или порог отсечения) равный – 0.614. В итоге мы получили регрессионные коэффициенты b и пороговое значение бинарного классификатора, что и завершает построение бинарного классификатора, после чего его можно использовать для классификации новых объектов.

ЭКАЗАМЕНАЦИОННЫЙ БИЛЕТ № 11

1. Модель классификатора с использованием «машины опорных векторов». Линейно разделимые множества.