13.Теоремы о производной суммы, произведения и частного.

1. Производная постоянной равна нулю, т.е. .

Правило, очевидно, так как любое приращение постоянной функции равно нулю.

2. Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций, т.е.

Пусть и - дифференцируемые функции. Найдем производную функции , используя схему вычисления производной.

Дадим аргументу приращение . Тогда функции и получат наращенные значения , , а функция - значение .

Находим приращение функции .

Составляем отношение .

Находим предел этого отношения при , т.е. .

3. Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, т.е. .

Пусть и - дифференцируемые функции. Найдем производную функции , используя схему вычисления производной.

Дадим аргументу приращение . Тогда функции и получат наращенные значения , , а функция - значение .

Находим приращение функции .

Составляем отношение .

Находим предел этого отношения при , т.е. .

4. Производная частного двух дифференцируемых функций может быть найдена по формуле: .

Следствие 1. Постоянный множитель можно выносить за знак производной: .

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.

Пример. Найти первую производную функции .

.

14. Производная сложной и обратной функции.

Теорема. Если и - дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и умноженной на производную самого промежуточного аргумента по независимой переменной , т.е. .

Теорема. Для дифференцируемой функции с производной, не равной нулю, производная обратной функции равна обратной величине производной данной функции, т.е. .

15. Дифференциал, связь дифференциала и приращения функции.

Определение. Дифференциалом функции называется главная, линейная относительно часть приращения функции, равная произведению производной на приращение независимой переменной .

Геометрический смысл дифференциала. Дифференциал функции есть приращение ординаты касательной, проведенной к графику функции в данной точке, когда получает приращение .

Свойства дифференциала:

1. .

2. .

3. .

4. .

5. .

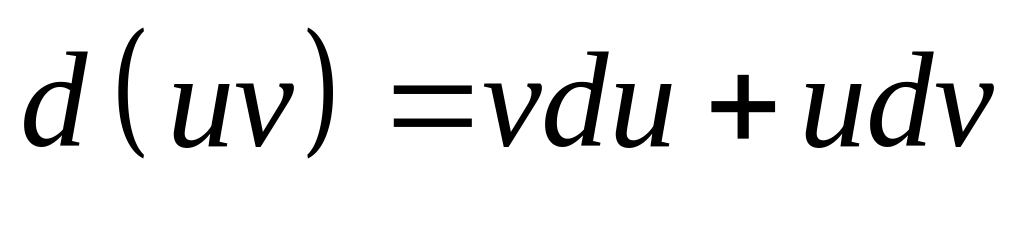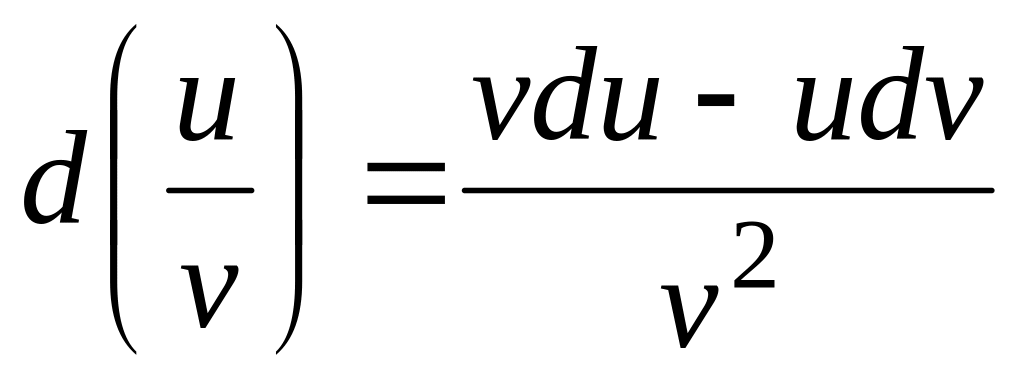Пример. Найти дифференциал функции .

Так как , то .

16.Производные и дифференциалы высших порядков.

Производной порядка называется производная от производной порядка.

Дифференциал второго порядка (или вторым дифференциалом) функции называется дифференциал от дифференциала первого порядка этой функции, т.е. .

Дифференциалом порядка (или дифференциалом) функции называется дифференциал от дифференциала порядка этой функции этой функции, т.е. .

Пример. Найти производную второго порядка функции .

Так как , то .