20. Закон распределения дискретной случайной величины.
-это
перечень её возможных значений и
соответствующие им вероятности. З-он
распределения ДСВ м.б. задан дискретно,
с помощью таблицы либо аналитическим
выражением (формулой). Если з-он задан
в виде таблицы, то 1-ая строка задаёт
возможное значение ДСВ, а 2-ая строка
соответствует вероятности. З-он
распределения ДСВ можно задать
графически, для этого в прямоугол. сист.
Координат строим 2 оси, по которым
откладываем возможное значение ДСВ.
Точки, соответствующие вероятности
соединяем и получаем многоугольное
распределение ДСВ.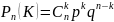
– биноминальный
закон распределения. Для ДСВ, когда
постоянная величина вероятности появл.
Соб.:
0<p<1
33.Правило 3.
Если СВ подчинена нормальному закону, то вероятность её отклонения от математического ожидания a>3, практически = 0 ≈0,027. Вероятность того, что СВ X задаётся нормальным законом распределения попадает в интервал 3 ≈ 1. Многие СВ распределяются нормально, или почти нормально.
Пример непрерывных СВ, распределённых по нормальному закону:
1)ошибки измерения;
2)ошибки стрельбы, вызванные наведением;
3)отклонения напряжения сети;
4)урожайность с/х культур
5)колебание курса валют;
6) рост М, Ж 1-го возраста, национальности (все количественные величины)
34. Закон больших чисел
Практика изучения случайных явлений показывает, что хотя результаты отдельных наблюдений, даже проведенных в одинаковых условиях, могут сильно отличаться, в то же время средние результаты для достаточно большого числа наблюдений устойчивы и слабо зависят от результатов отдельных наблюдений. Теоретическим обоснованием этого свойства случайных явлений является закон больших чисел. Общий смысл закона больших чисел - совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая. Простейшая форма закона больших чисел, и исторически первая теорема этого раздела - теорема Бернулли, утверждающая, что если вероятность события одинакова во всех испытаниях, то с увеличением числа испытаний частота события стремится к вероятности события и перестает быть случайной. Теорема Пуассона утверждает, что частота события в серии независимых испытаний стремится к среднему арифметическому его вероятностей и перестает быть случайной. Предельные теоремы теории вероятностей, теоремы Муавра-Лапласа объясняют природу устойчивости частоты появлений события. Природа эта состоит в том, что предельным распределением числа появлений события при неограниченном возрастании числа испытаний (если вероятность Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая. На этом свойстве основаны методы оценки вероятности на основе анализа конечной выборки. Наглядным примером является прогноз результатов выборов на основе опроса выборки избирателей.