P=m/n – число, характеризующее степень возможности появления события.

1.Теорема сложения вероятностей несовместных событий P(A+B).

Если события А и В несовместны, то А+В для несовместных событий означает появление или события А, или события В. Вероятность появления 1-го из 2-ух несовместных событий безразлично какого = сумме вероятностей этих событий: P (A+B) = Р(А)+Р(В)

2.Теорема умножения вероятностей независимых событий.

Вероятность появления 2-ух независимых событий = произведению вероятностей этих событий:

P (A*B) = P (A)*P (B)

(A*B) означает события, состоящие в появлении этих 2-ух событий одновременно. Например: бросили монету 3 р., А – выпадение герба в 1 случае, В – во 2-ом, С – в 3-ем.

АВС – выпал герб во всех 3-ёх случаях.

3. Полная группа событий.

Несколько событий образуют полную. Гр., если в результате испытания появится хотя бы 1 из них. Пример: бросаем монету. Возможны 2 события:

- выпал орёл;

- выпала решка;

2 события образуют полную гр. Событий

4.Противоположные события P (A) + P ( ) = 1

Противоположным событием называют 2 единственно возможных события, образующих полную группу. Событие А – противоположное событие, событие 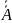- не выпадение.

Теорема: сумма вероятностей противоположного события = 1:

5.Вероятность появления хотя бы одного события P (A) = 1 –

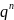
Теорема: вероятность появления хотя бы 1-го из нескольких независимых событий = разности между 1 и произведением вероятностей противоположного события:

P (A) = 1- , ,…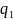

= =

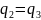P (A) = 1 -

6. Формулы комбинаторики

	Упорядоченная совокупность	Неупорядоченная совокупность
Без повторений	1)Размещение без повторений: = 2) Число перестановок без повторений:	5)Число сочетаний из n элементов по m без повторений:
С повторением	3) Число перестановок с повторениями: 4) Число размещений из n элементов по m с повторениями: =	6)Число сочетаний из n элементов по m без повторений: → →

7.

8. Формула полной вероятности

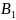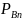P (A) = P ( ) (A) + P ( ) (A) +…+ P ( ) (A)

Формула полной вероятности позволяет вычислить вероятность интересующего события через условные вероятности этого события в предположении неких гипотез, а также вероятностей этих гипотез.

Допустим, что событие А произошло!

Определим: как именится вероятность появления 1-го из событий ( , ), другими словами определим вероятность 1-ой из гипотез, т.е.: ( ) ( ) ( ). Эти вероятности являются условными. Вероятность 1-ой из гипотез показывает, какова вероятность появления или проявления события при условии, что число событий А – произошло.

16. Локальная теорема Лапласа.

Если в каждом испытании вероятность появления события А постоянна и эта вероятность отлична от 0 и 1, то вероятность появления события А k раз в n испытании ≈ значению следующей функции:

P (A) = p

p≠0 и p≠1

≈ * - *

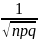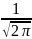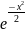
Для этой функции имеется таблица, т.к. она чётная.
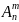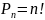
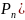
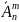
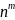