
РГР Интегралы
.docТеоретический вопрос
I. Интегрирование выражений R(sinx, cosx)
Пусть R(u,v) — рациональная функция двух переменных. Положим u = sin< var>x и v = cos x . Получится функция f(x) = R(sin x, cos x) . Она имеет период 2π . Поэтому ее первообразные достаточно найти на интервале ( −π, π) .
Интеграл от функции R(sinx, cosx) с помощью подстановки всегда приводится к интегралу от рациональной функции переменной t. Поэтому он выражается через элементарные функции .
Подстановка (1) называется универсальной.
Если подынтегральная функция R(sinx, cosx) имеет специальный вид, то можно применить методы, требующие меньше преобразований, чем при использовании универсальной подстановки.
1. Если R(u, v) нечетна относительно v , то существует рациональная функция Rs(u, v)
R(u, v) = Rs(u, v2) · v .
Поэтому
|
|
∫ R(sin x, cos x) dx = ∫ Rs(sin x, cos2x) cos x dx . |
|
Подводя cos x под знак дифференциала, получаем
|
|
∫ R(sin x, cos x) dx = ∫ Rs(sin x, cos2x) dsin x . |
|
Очевидно, что замена переменной t = sin x сводит задачу к интегрированию рациональной функции:
|
|
∫ R(sin x, cos x) dx = ∫ Rs( t, 1 − t2 ) dt при t = sin x . |
|
2. Если R(u, v) нечетна относительно u , то существует рациональная функция Rs(u, v) , такая что
R(u, v) = Rs(u2, v) · u .
Поэтому
|
|
∫ R(sin x, cos x) dx = ∫ Rs(sin2x, cos x) sin x dx . |
|
Подводя sin x под знак дифференциала, получаем
|
|
∫ R(sin x, cos x) dx = − ∫ Rs(sin2x, cos x) dcos x . |
|
Очевидно, что замена переменной t = cos x сводит задачу к интегрированию рациональной функции:
|
|
∫ R(sin x, cos x) dx = − ∫ Rs(1 − t2, t) dt при t = cos x . |
|
3. Если R(u, v) = R( − u, − v) , то существует рациональная функция Rs( · ) одной переменной, такая что R(u, v) = Rs(u / v) . Поэтому
|
|
∫ R(sin x, cos x) dx = ∫ Rs(tg x) dx . |
|
Функция Rs(tg x) периодична с периодом π . Поэтому допустима подстановка
|
|
x = arctg t t = tg x x О ( −π / 2, π / 2 ) t О ( −∞, +∞) |
|
II. Интегрирование выражений sin2mx · cos2nx
Интегралы вида
|
|
∫ sin2mx · cos2nx dx, |
|
где m и n — натуральные числа, находятся с использованием формул понижения степени:
III. Интегрирование выражений вида sin (αx) · sin (βx) , sin (αx) · cos (βx) , cos (αx) · cos (βx) .
При интегрировании этих выражений используются тригонометрические формулы.
Расчетные задания
Задача 1. Вычислить неопределенный интеграл.

Задача 2. Вычислить определенный интеграл.
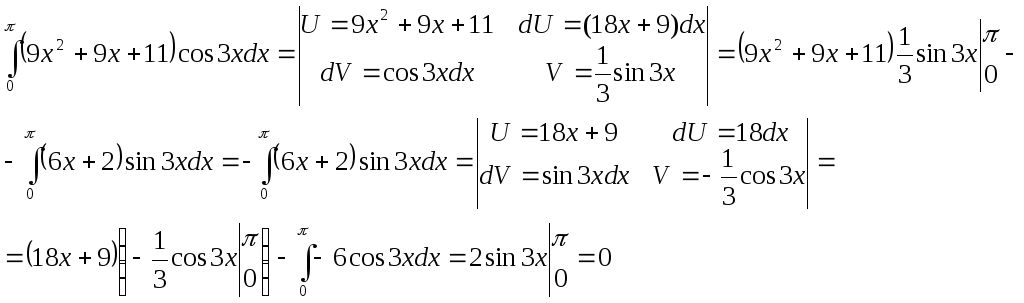
Задача 3. Найти неопределенный интеграл.

Задача 5. Вычислить неопределенный интеграл.
![]()
![]()
![]()
![]()
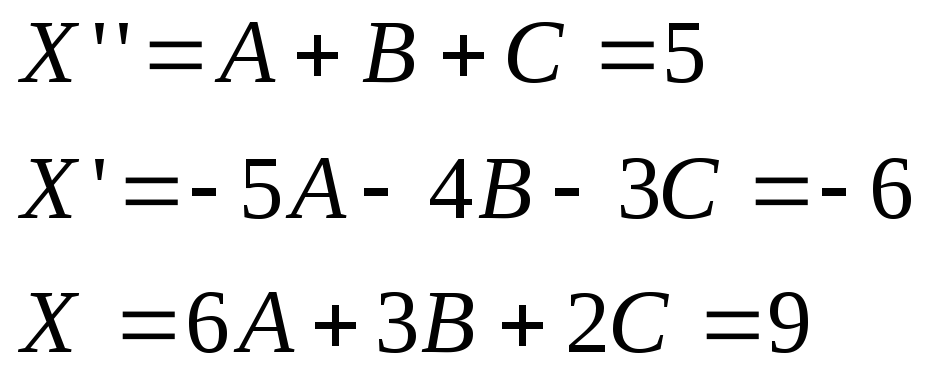

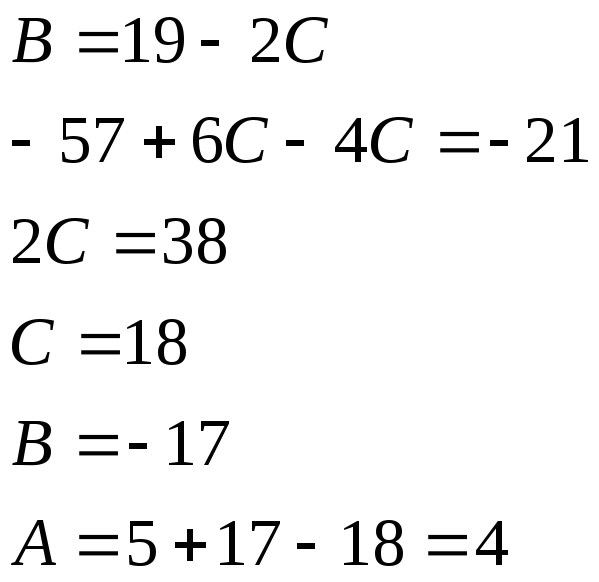
![]()
Задача 6. Вычислить неопределенный интеграл.

![]()
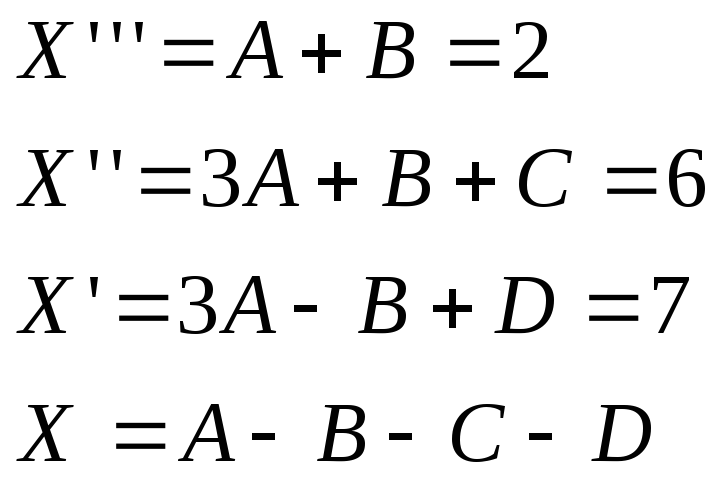

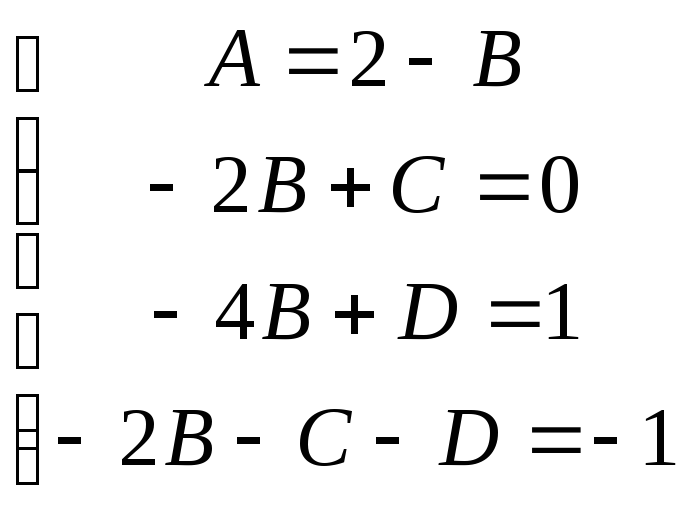


![]()
Задача 10. Вычислить определенный интеграл.

Задача 13. Вычислить определенный интеграл.
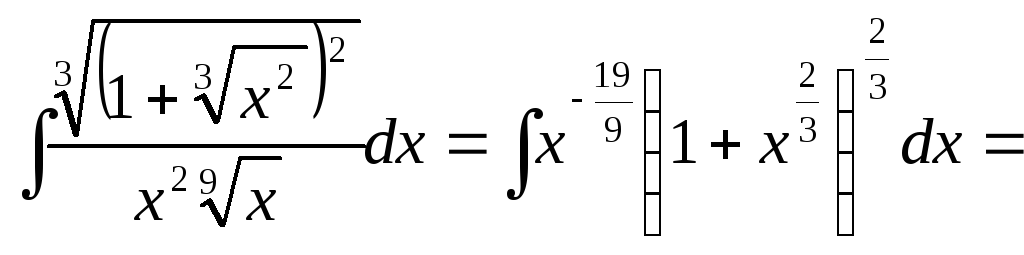
![]()
![]()
![]()
![]()
![]()
=
