
Общее равновесие, эффективность и общественное благосостояние
Общее и частичное равновесие. Модель Вальраса. Существование и стабильность и условия общего равновесия.
Общее равновесие и эффективность. Оптимальность по Парето. Коробка Эджуорта. Контрактная кривая.
Теоремы экономической теории благосостояния.
Теория общественного благосостояния. Понятие эффективности и справедливости в теории общественного благосостояния.
Литература:
50 лекций по микроэкономике. - лекции 41 – 42 ???
Чеканский – раздел VI
Самостоятельно:
Модель Д. Бредфорда противоречия и согласование моделей частичного и общего равновесия. – Фридмен лекция 15
Модель рыночного социализма (О.Ланге, АЛернер и др.) – Нуреев
Рассмотреть тенденцию к общему равновесию при симметрично разнонаправленном и ассиметричном взаимодействии – 24.1.3 – 24.1.4 Чеканский
Роулсианский подход к оценке общественного благосостояния.
Равноправное и справедливое распределение Х. Вэриана.
Механизмы перераспределения доходов.
Теорема невозможности Эрроу
Исследуя частичное равновесие мы использовали метод «при прочих равных» (Caeteris paribus), рассматривали равновесие отдельного субъекта или рынка, принимая предпосылку о заданности переменных – например, пытались определить потребительский выбор индивида при заданной величине его дохода и ценах потребительских благ, предполагая, что выбор этого индивида не оказывает никакого влияния на эти переменные. Сняв это предположение, мы оказываемся в море взаимосвязей, где "все зависит от всего" и изменение любой переменной влечет за собой изменение многих других переменных хозяйства.
Достижение общего равновесия - результат воздействия изменения на одном рынке на все другие рынки, в том числе и на тот рынок, с которого началось движение. Многообразные связи между рынками различных товаров и услуг можно разделить на прямые и обратные. Через прямые связи первоначальные изменения цены какого-либо блага влияют на рынки других благ. Посредством обратных связей осуществляется обратное влияние изменений на рынках этих других благ на первоначальный рынок.
В этом взаимодействии на передний план выходят взаимозависимость и взаимодополняемость различных товаров. Поэтому простейший анализ должен включать как минимум четыре этапа:
1. Первичное изменения;
2. Рынки взаимозаменяющих товаров;
3. Рынки взаимодополняющих товаров;
4. Эффект обратной связи.
Рассмотрим условный пример с ростом цен на автомобили. «Допустим, что цена на автомобиль поднялась с 7000 до 10000 долл. Это вызовет снижение продаж с 20 млн. автомобилей в год до 15 млн. (см. рис.10-1а). Падение спроса на автомобили отразится на спросе на бензин. Он сократится с 12 млн. до 10 млн. л в день. Это выразится в падении цены бензина с 30 до 40 центов за литр. (см. рис 10-16).
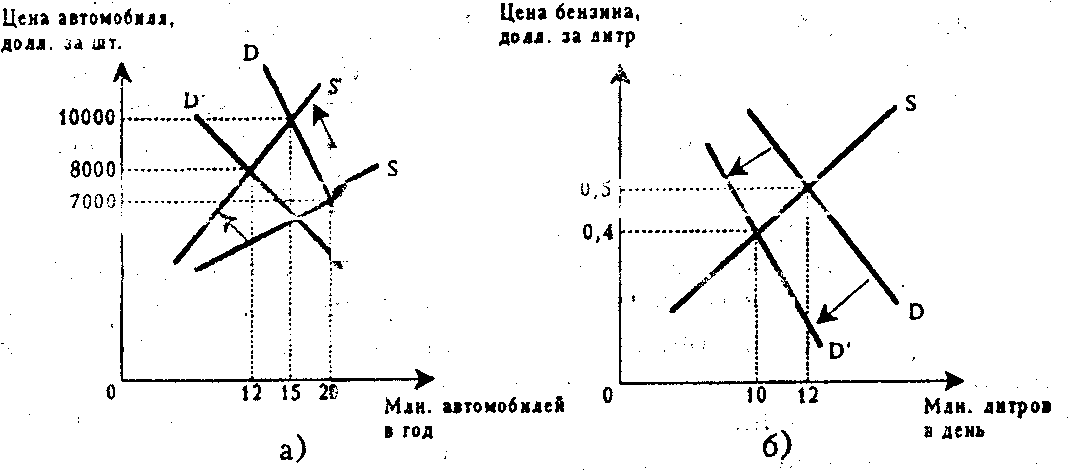
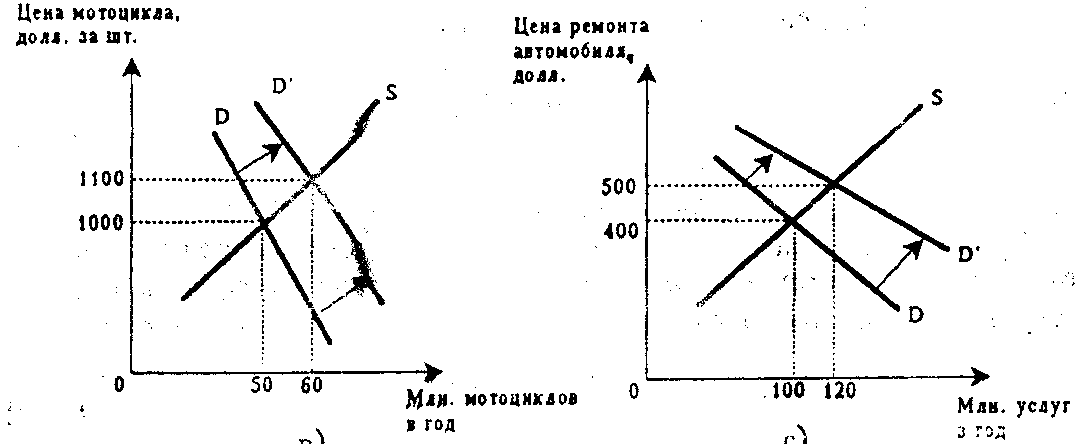
Рост цен на автомобили заставит многих отказаться от покупки нового автомобиля и обратить взоры на товары-заменители. Т.о. высокая цена на автомобиль расширит спрос на мотоциклы и заставит дольше эксплуатировать старые машины. Допустим, спрос на мотоциклы возрастет с 50 млн. до 60 млн. мотоциклов в год (см. рис. 10-1в). Это поднимет цену мотоцикла в среднем с 1000 до 1100 долл.
Более длительное использование старых автомобилей приведет к росту цен на услуги по ремонту вследствие увеличения спроса на такие услуги. Их число возрастет со 100 млн. до 120 млн. в год, а цена на них в среднем поднимется с400-до 500 долл. В результате более продолжительного использования старых автомобилей и расширения спроса на мотоциклы спрос на новые автомобили упадет до 12 млн в год. Это заставит производителей снизить цену с 10000 до 8000 долл (см. рис.10-1а).
Естественно, такое изменение равновесной цены вызовет новую реакцию на рынках взаимодополняющих и взаимозаменяющих товаров, которая приведет к установлению новых равновесных цен и объемов на всех рынках.
В нашем примере проанализирована взаимосвязь лишь четырех рынков. В действительности структура подобных взаимосвязей значительно сложнее. Однако даже приведенный условный пример наглядно показывает, что равновесные цены и количества определяются с учетом эффекта обратной связи (feedback effect), отражающем изменение частичного равновесия на данном рынке в результате изменений, возникших на сопряженных рынках под влиянием первоначальных изменений на данном рынке.
Анализ общего равновесия показал, что уменьшение предложения и соответствующий рост цен на некотором рынке приводят к падению, спроса на дополняющие товары и его росту на товары-субституты.
В зависимости от особенностей сочетания прямых и обратных связей межрыночные взаимодействия можно подразделить на:
Ассиметричные – такое межрыночное взаимодействие, при котором прямые и обратные связи действуют в разных направлениях, для них характерен различный тип зависимости между ценами на сопряженные товары.
PA ↑ → PB ↓ → PA ↓
Симметричные – такое межрыночное взаимодействие, при котором прямые и обратные связи действуют в одном и том же направлении.
Симметрично однонаправленные связи: PA ↑ → PB ↑ → PA ↑
Симметрично разнонаправленные связи: PA ↑ → PB ↓ → PA ↑
Рассмотрим тенденцию к общему равновесию при симметрично однонаправленном взаимодействии на примере рынков товаров-субститутов. Для этого введем термин избыточный спрос (ED) - разница между величиной спроса и предложения. Избыточный спрос находиться в обратной зависимости от цены:
- если цена ниже равновесной на данном рынке XD > XS => ED > 0
- если цена равна равновесной на данном рынке XD = XS => ED = 0
- если цена выше равновесной на данном рынке XD < XS => ED < 0
График избыточного спроса имеет вид:
Рисунок 24.1 б
Допустим, что цена на товар Y, являющийся товаром-заменителем для Х, выросла. Это увеличит спрос на товар Х, т.е. сдвинет кривую спроса вправо-вверх (D1). Соответственно возрастет равновесная цена, а график избыточного спроса сдвинется вправо-вверх (ED1).
Графическое отражение зависимости между ценой блага Y и равновесной ценой блага X, все точки которой означают нулевой избыточный спрос (EDX = 0) назовем кривой частичного равновесия по благу Х – она представляет все возможные значения цен на благо Х при различных значениях цен на благо Y.
Чем выше PY , тем выше равновесная PX.
Все точки слева от кривой отражают такие сочетания PX и PY при которых существует избыточный спрос на благо Х (PX оказываются меньше равновесной).
Все точки справа от кривой отражают такие сочетания PX и PY при которых существует избыточное предложение на благо Х (PX оказываются больше равновесной).

Рассмотрим зависимость равновесной цены товара Y, при которой избыточный спрос на него равен нулю (EDY = 0), от цены товара Х.
Чем выше PX , тем выше равновесная PY. – т.к. Х и Y – субституты.
Точка пересечения EDY = 0 с осью PY отражает равновесную цену на рынке товара Y , которая сложилась бы при бесплатной раздаче товара X.
Все точки ниже (справа) от кривой отражают такие сочетания PX и PY при которых существует избыточный спрос на благо Y (PY оказываются меньше равновесной).
Все точки выше (слева) от кривой отражают такие сочетания PX и PY при которых избыточный спрос на благо Y отрицателен (PY оказываются больше равновесной).
Т.о. координаты точки общего равновесии мы получим при пересечении кривых EDХ = 0 и EDY = 0. Пересечение этих кривых возможно только если тангенс угла наклона1 EDХ = 0 больше соответствующего показателя EDY = 0, т.е. кривая EDХ = 0 круче кривой EDY = 0.
Логично предположить, что на спрос на какой-либо товар изменение его собственной цены оказывает большее влияние, чем изменение цены товара-заменителя, т.е. прямые ценовые эффекты влияют сильнее, чем перекрестные. Следовательно, чтобы обеспечить увеличение спроса на яблоки на 10%, цена на груши должна вырасти больше, например на 20%, чем может снизиться цена на яблоки, например на 8%, приведшая к такому же увеличению спроса на них.
Следовательно,
тангенс угла наклона EDХ
= 0 будет всегда больше единицы
 >1 , а тангенс
угла наклона EDY
= 0 будет всегда меньше единицы
< 1 .
>1 , а тангенс
угла наклона EDY
= 0 будет всегда меньше единицы
< 1 .

Допустим, что общее равновесие на достигнуто и рынок характеризуется точкой F. На рынке товара Х существует избыточное предложение и имеется тенденция к уменьшению цены Х, а на рынке товара Y существует избыточный спрос и имеется тенденция к увеличению цены Y.
Т.о. при симметрично однонаправленном межрыночном взаимодействии общее равновесие существует, оно стабильно и действует объективная тенденция к его достижению.
Теперь выразим алгебраически модель общего равновесия.
Взаимосвязь товарных рынков может быть записана системой уравнений. Первым, кто попытался описать экономическое равновесие с помощью системы уравнений, был швейцарский экономист Леон Вальрас (1834-1910). В рыночной экономике цены предопределяют объем выпускаемой продукции, а объем выпуска в значительной степени определяет цены. Цены потребительских товаров и услуг зависят от цен ресурсов. А цены ресурсов - от цен потребительских благ, на которые существует платежеспособный спрос. Взаимосвязь в экономике оборачивается порочным кругом, выйти из которого можно, лишь решая всю систему уравнений одновременно.
Представлена система уравнений для 10 000 товаров:

где А - показатель реальных активов, отражающий богатство страны, М - запас наличных денег. Если известны А и М, то число уравнений равно числу неизвестных. Это означает, во-первых, принципиальную возможность решения системы (то есть достижения общего равновесия) и, во-вторых, единственность такого решения.
При этом функция спроса линейно однородна, т.е. равновесные цены останутся равновесными независимо от того в каких денежных единицах они выражены – рублях, долларах, у.е., а экономические агенты реагируют на относительные цены, а не на абсолютные.
Формализуем решение. Пусть в экономике имеется N товаров, включая ресурсы, значит N рынков и N цен. Тогда спрос и предложение на каждый i-тый товар можно записать:
Di = f(P1, P2, … PN)
Si = f(P1, P2, … PN)
Обозначим вектор цен через P и выразим избыточный спрос:
EDi (P) = Di (P) - Si (P)
Требуется доказать, что существует такой набор цен P* при котором одновременно достигается равновесие на всех рынках, т.е. Edi (P*) = 0. Поскольку i = 1, 2, …, N, то существует N уравнений. Уравнения системы связаны зависимостью, которую называют законом Вальраса: стоимость совокупного избыточного спроса равна нулю при любых ценах на товар.
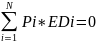
Доказательство: доход каждого индивида формируется только от продажи каких-то благ, в число которых входят факторы производства, поэтому бюджетное ограничение каждого индивида всегда характеризуется равенством стоимости покупок и стоимостью продаж.
Просуммировав это выражение для всех субъектов (m), получим:
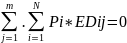
Из закона Вальраса вытекает, что если на N-1 рынках достигается равновесие, то и на последнем рынке N достигается равновесие.
Во времена Вальраса отсутствовал математический аппарат для решения такой системы. Поэтому решение системы Л.Вальрас видел в группировке уравнений. Путь к равновесию рассматривался им как постепенный процесс, который он обозначал французским словом tatonnement - "нащупывание", "поиск ощупью" верных пропорций обмена.
Выбирается произвольная совокупность цен (P1, P2, … , PN). Предполагая N-1 цен неизменными находим равновесную цену на первом рынке, затем на втором и так далее. Полученный вектор цен (P*1, P*2, … , P*N) не будет равновесным, поэтому повторим расчет: найдем цену P**1 считая все остальные цены неизменными, затем P**2 и так далее. Каждый раз после итерации вектор цен будет все ближе к значениям равновесных цен.
Конечно, модель Л. Вальраса несколько идеализировала действительность. В ней предусматривалось, что потребители знают свои функции спроса и предложения, технических коэффициенты и многие другие данные. Модель общего равновесия исходит из совершенной конкуренции, предполагающей идеальную мобильность всех ресурсов, полную информированность участников, абсолютизирует состояние равновесия, тогда как в реальной действительности гораздо чаще встречаются диспропорции и дисбалансы. К тому же она статична, так как не учитывает научно-технического прогресса, факторов неопределенности в экономике, институциональных условий развития.
Модель Вальраса описывает реальный процесс взаимодействия рынков на пути к поэтапному приближению к равновесию. Анализ этого процесса привел его к правильному выводу о том, что система общего равновесия устойчива, и, будучи выведена из этого состояния, стремится к нему вновь через механизм относительных цен.
Эту мысль можно упрощать и усложнять путем включения в нее новых переменных. Последние могут задаваться как эндогенно, так и экзогенно, отражать как экономические процессы и явления, так и институциональные условия функционирования рыночной экономики.
Важно подчеркнуть, что Л. Вальрас указал современной экономической науке путь, по которое, как справедливо заметил Й. Шумпетер, она идет и сегодня.
Условия достижения общего равновесия включает неизменность решений
покупателей относительно количеств товаров, которые они желают приобрести. |
Продавцов относительно объемов предложения своих товаров. |
Покупатели максимизируют полезность, т.е. достигают равновесия в точке |
Продавцы максимизируют прибыль, т.е. достигают равновесия в точке |
MRSx,y = Px / Py Т.к. при совершенной конкуренции цены одинаковы для всех потребителей, то можно утверждать, что в условиях общего равновесия MRS для всех потребителей любой пары товаров тоже будут одинаковы. |
Pi = MCi – условие max PR MRTSK,L = w / r – условие min издержек Условием общего равновесия можно считать равенство MRTSK,L в производстве любой продукции. |
Где - альтернативная стоимость блага X, показывает каким количеством блага Y нужно пожертвовать, чтобы за счет высвободившихся ресурсов увеличить выпуск блага Х на единицу, или предельная норма трансформации Y в Х MRTx,y = |
|
MRTx,y = = MRSx,y В условиях общего равновесия для любой пары благ предельная норма замещения в производстве (MRT) должна быть равна предельной норме замещения в потреблении (MRS). |
|

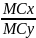 =
=
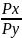 = MRSx,y
= MRSx,y