Тема: Элементы специальной теории относительности

-мезон, двигавшийся со скоростью  (с – скорость света в вакууме) в лабораторной системе отсчета, распадается на два фотона: ₁ и ₂. В системе отсчета мезона фотон ₁ был испущен вперед, а фотон ₂ – назад относительно направления полета мезона. Скорость фотона ₂ в лабораторной системе отсчета равна …

Решение: Фотон является частицей, которая может существовать, только двигаясь со скоростью с, то есть со скоростью света в вакууме. Кроме того, согласно одному из постулатов специальной теории относительности – принципу постоянства скорости света, скорость света в вакууме не зависит от движения источника света и, следовательно, одинакова во всех инерциальных системах отсчета. Поэтому скорость фотона ₂ с учетом направления его движения в лабораторной системе отсчета равна: .

Тема: Элементы специальной теории относительности Объем воды в Мировом океане равен 1,37·10⁹ км³. Если температура воды повысится на 1°С, увеличение массы воды составит _______ . (Плотность морской воды 1,03 г/см³, удельная теплоемкость 4,19 кДж/(кг·К).)

			6,57·107 кг
			65,7 т
			65,7 кг
			6,57·10-2 кг

Решение: Из закона взаимосвязи массы и энергии следует, что изменение энергии покоя сопровождается изменением массы тела, причем эти изменения пропорциональны друг другу: , где  – скорость света в вакууме. Изменение температуры воды в Мировом океане означает, что вода получила количество теплоты, равное , где  – удельная теплоемкость воды,  – ее плотность,  – объем. Тогда увеличение массы воды составит

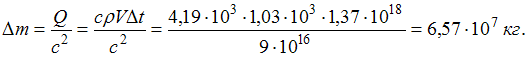
Тема: Элементы специальной теории относительности Нестабильная частица движется со скоростью 0,6 с (с – скорость света в вакууме). Тогда время ее жизни в системе отсчета, относительно которой частица движется ______%.

			увеличится на 25
			уменьшится на 25
			уменьшится на 40
			увеличится на 40

ема: Элементы специальной теории относительности Частица движется со скоростью 0,8 с (с – скорость света в вакууме). Тогда ее масса по сравнению с массой покоя ______%.

			увеличится на 67
			уменьшится на 67
			увеличится на 33
			уменьшится на 33

Тема: Динамика вращательного движения 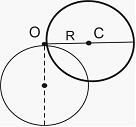Диск радиусом 1 м, способный свободно вращаться вокруг горизонтальной оси, проходящей через точку О перпендикулярно плоскости рисунка, отклонили от вертикали на угол  и отпустили. В начальный момент времени угловое ускорение диска равно _______ 

			7
			10
			5
			20

Решение: 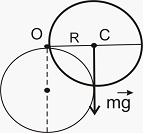Момент силы тяжести относительно оси, проходящей через точку О, равен , где радиус диска и плечо силы. Момент инерции диска относительно оси, проходящей через центр тяжести (точку С), равен 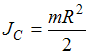; а момент инерции обруча относительно оси, проходящей через точку О, найдем по теореме Штейнера: 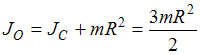. Используя основной закон динамики вращательного движения твердого тела вокруг неподвижной оси, можем определить угловое ускорение:   .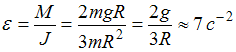

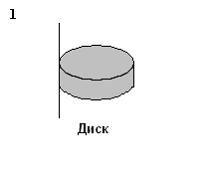
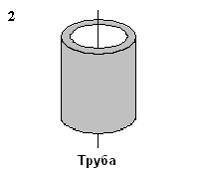
Тема: Динамика вращательного движения Рассматриваются три тела: диск, тонкостенная труба и сплошной шар; причем массы m и радиусы R шара и оснований диска и трубы одинаковы. 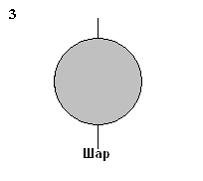Верным для моментов инерции рассматриваемых тел относительно указанных осей является соотношение …

Решение: Момент инерции сплошного однородного кругового цилиндра (диска) массы m и радиуса R относительно его оси . Момент инерции диска относительно указанной оси вычисляется с использованием теоремы Штейнера: . Момент инерции тонкостенного кругового цилиндра массы m и радиуса R относительно его оси , момент инерции шара массы m и радиуса R . Таким образом, правильным соотношением для моментов инерции рассматриваемых тел относительно указанных осей является соотношение .

Тема: Динамика вращательного движения Если ось вращения тонкостенного кругового цилиндра перенести из центра масс на образующую (рис.), то момент инерции относительно новой оси _____ раза.

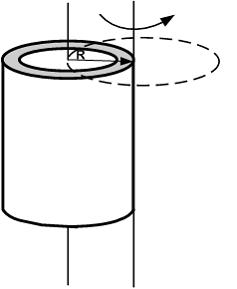
			увеличится в 2
			уменьшится в 2
			увеличится в 1,5
			уменьшится в 1,5

Тема: Динамика вращательного движения Направления векторов момента импульса  и момента силы для равнозамедленного вращения твердого тела правильно показаны на    рисунке …

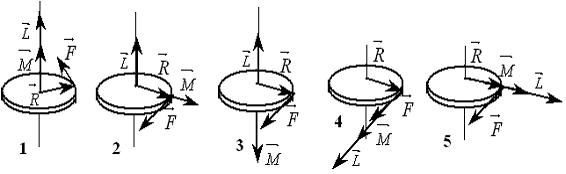
			3
			1
			2
			4
			5

Решение: Момент силы  определяется соотношением , где  – радиус-вектор точки приложения силы. Направление вектора момента силы можно определить по правилу векторного произведения или по правилу правого винта (буравчика). Таким образом, момент силы направлен вдоль оси вращения. Согласно основному закону динамики вращательного движения твердого тела, , где момент инерции тела, вектор углового ускорения, который сонаправлен с вектором момента силы. Момент импульса равен , где вектор угловой скорости, который по правилу правого винта направлен вдоль оси вращения, следовательно, и вектор момента импульса направлен так же. Поскольку вращение равнозамедленное,  вектор углового ускорения направлен противоположно вектору угловой скорости, значит, векторы  и  противоположны. Условию задачи соответствует рисунок 3.