Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга

Ширина следа электрона на фотографии, полученной с использованием камеры Вильсона, составляет  Учитывая, что постоянная Планка , а масса электрона  неопределенность в определении скорости электрона будет не менее …

Решение: Из соотношения неопределенностей Гейзенберга для координаты и соответствующей компоненты импульса следует, что , где  – неопределенность координаты,  – неопределенность x-компоненты импульса,  – неопределенность x-компоненты скорости,  – масса частицы;  – постоянная Планка, деленная на . Неопределенность x-компоненты скорости электрона можно найти из соотношения

Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга

Неопределенность в определении местоположения частицы, движущейся вдоль оси x, равна длине волны де Бройля для этой частицы. Относительная неопределенность ее скорости не меньше _____ %.

			16
			100
			32
			8

Решение: Из соотношения неопределенностей Гейзенберга для координаты и соответствующей компоненты импульса следует, что .  Здесь  – неопределенность координаты,  – неопределенность x-компоненты импульса,  – неопределенность x-компоненты скорости,  – масса частицы;  – постоянная Планка, деленная на . По условию , где  – длина волны де Бройля, определяемая соотношением . Здесь  – постоянная Планка. Подставляя это выражение в соотношение неопределенностей, получаем: .

Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга

Если протон и дейтрон прошли одинаковую ускоряющую разность потенциалов, то отношение их длин волн де Бройля равно …

			1
			2

Решение: Дейтрон – ядро тяжелого изотопа водорода (дейтерия). Длина волны де Бройля определяется по формуле , где p – импульс частицы. Импульс частицы можно выразить через ее кинетическую энергию: . По теореме о кинетической энергии, согласно которой работа сил электрического поля идет на приращение кинетической энергии, . Отсюда можно найти , полагая, что первоначально частица покоилась:  Окончательное выражение  для длины волны де Бройля через ускоряющую разность потенциалов имеет вид  Учитывая, что  и  отношение длин волн де Бройля протона и дейтрона равно:

Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга Положение пылинки массой можно установить с неопределенностью . Учитывая, что постоянная Планка , неопределенность скорости    (в м/с) будет не менее …

Решение: Из соотношения неопределенностей Гейзенберга для координаты и соответствующей компоненты импульса  следует, что , где  – неопределенность координаты,  – неопределенность x-компоненты импульса,  – неопределенность x-компоненты скорости,  – масса частицы;  – постоянная Планка, деленная на . Неопределенность x-компоненты скорости пылинки можно найти из соотношения

Тема: Уравнение Шредингера (конкретные ситуации) Квантовая и классическая частицы с энергией Е, движущиеся слева направо, встречают на своем пути потенциальный барьер высоты  и ширины . 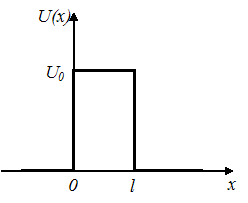Если  P − вероятность преодоления барьера, то для …

			квантовой частицы при   , а при
			классической частицы при   , а при
			квантовой частицы при   , а при
			квантовой частицы  зависит только от  и не зависит от

Решение: Поведение микрочастицы, встречающей на своем пути потенциальный барьер, существенно различается с точки зрения классической и квантовой механики. По классическим представлениям, если энергия частицы больше высоты барьера ( ), частица беспрепятственно проходит над барьером, то есть вероятность преодоления барьера . Если же , то частица отражается от барьера, сквозь барьер она проникнуть не может и . Согласно квантовой механике даже при  имеется отличная от нуля вероятность отражения частицы от барьера и, следовательно, вероятность преодоления барьера . При  имеется отличная от нуля вероятность того, что частица проникнет сквозь барьер и окажется в области, где , то есть .

Тема: Уравнение Шредингера (конкретные ситуации) Момент импульса электрона в атоме и его пространственные ориентации могут быть условно изображены векторной схемой, на которой длина вектора пропорциональна модулю орбитального момента импульса  электрона. На рисунке приведены возможные ориентации вектора . 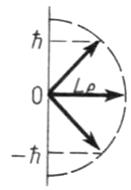Значение орбитального квантового числа и минимальное значение главного квантового числа для указанного состояния соответственно равны …

			,
			,
			,
			,

Тема: Уравнение Шредингера (конкретные ситуации) Частица находится в прямоугольном одномерном потенциальном ящике с непроницаемыми стенками шириной 0,2 нм. Если энергия частицы на втором энергетическом уровне равна 37,8 эВ, то на четвертом энергетическом уровне равна _____ эВ.

			151,2
			75,6
			18,9
			9,45

Решение: Собственные значения энергии частицы в прямоугольном одномерном потенциальном ящике определяются формулой: , где номер энергетического уровня. Следовательно,  и .