
- •Кинематика поступательного и вращательного движения
- •Тема: Кинематика поступательного и вращательного движения
- •Тема: Кинематика поступательного и вращательного движения
- •Тема: Кинематика поступательного и вращательного движения
- •Тема: Кинематика поступательного и вращательного движения
- •Тема: Кинематика поступательного и вращательного движения
- •Тема: Элементы специальной теории относительности
- •Тема: Элементы специальной теории относительности
- •Тема: Элементы специальной теории относительности
- •Тема: Элементы специальной теории относительности
- •Тема: Динамика вращательного движения
- •Тема: Динамика вращательного движения
- •Тема: Динамика вращательного движения
- •Тема: Динамика вращательного движения
- •Тема: Динамика вращательного движения
- •Тема: Законы сохранения в механике
- •Тема: Законы сохранения в механике
- •Тема: Законы сохранения в механике
- •Тема: Законы сохранения в механике
- •Тема: Распределения Максвелла и Больцмана
- •Тема: Распределения Максвелла и Больцмана
- •Тема: Распределения Максвелла и Больцмана
- •Тема: Распределения Максвелла и Больцмана
- •Тема: Распределения Максвелла и Больцмана
- •Тема: Средняя энергия молекул
- •Тема: Средняя энергия молекул
- •Тема: Средняя энергия молекул
- •Тема: Средняя энергия молекул
- •Тема: Средняя энергия молекул
- •Тема: Средняя энергия молекул
- •Тема: Первое начало термодинамики. Работа при изопроцессах
- •Тема: Электростатическое поле в вакууме
- •Тема: Электростатическое поле в вакууме
- •Тема: Электростатическое поле в вакууме
- •Тема: Законы постоянного тока
- •Тема: Законы постоянного тока
- •Тема: Законы постоянного тока
- •Тема: Законы постоянного тока
- •Тема: Магнитостатика
- •Тема: Явление электромагнитной индукции
- •Тема: Магнитостатика
- •Тема: Магнитостатика
- •Тема: Явление электромагнитной индукции
- •Тема: Явление электромагнитной индукции
- •Тема: Уравнения Максвелла
- •Тема: Уравнения Максвелла
- •Тема: Уравнения Максвелла
- •Тема: Сложение гармонических колебаний
- •Тема: Сложение гармонических колебаний
- •Тема: Сложение гармонических колебаний
- •Тема: Свободные и вынужденные колебания
- •Тема: Волны. Уравнение волны
- •Тема: Волны. Уравнение волны
- •Тема: Энергия волны. Перенос энергии волной
- •Тема: Интерференция и дифракция света
- •Тема: Интерференция и дифракция света
- •Тема: Интерференция и дифракция света
- •Тема: Поляризация и дисперсия света
- •Тепловое излучение. Фотоэффект
- •Тема: Тепловое излучение. Фотоэффект
- •Тема: Эффект Комптона. Световое давление
- •Тема: Тепловое излучение. Фотоэффект
- •Тема: Эффект Комптона. Световое давление
- •Тема: Эффект Комптона. Световое давление
- •Тема: Тепловое излучение. Фотоэффект
- •Тема: Спектр атома водорода. Правило отбора
- •Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
- •Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
- •Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
- •Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
- •Тема: Уравнения Шредингера (общие свойства)
- •Тема: Уравнение Шредингера (конкретные ситуации)
- •Тема: Уравнения Шредингера (общие свойства)
- •Тема: Уравнение Шредингера (конкретные ситуации)
- •Тема: Уравнения Шредингера (общие свойства)
- •Тема: Уравнение Шредингера (конкретные ситуации)
- •Тема: Уравнение Шредингера (конкретные ситуации)
- •Тема: Уравнения Шредингера (общие свойства)
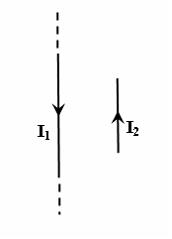
Тема: Магнитостатика
Поле
создано прямолинейным длинным проводником
с током I1. Если отрезок
проводника с током I2
расположен в одной плоскости с длинным
проводником так, как показано на рисунке,
то сила Ампера …
|
|
|
лежит в плоскости чертежа и направлена вправо |
|
|
|
лежит в плоскости чертежа и направлена влево |
|
|
|
перпендикулярна плоскости чертежа и направлена «от нас» |
|
|
|
перпендикулярна плоскости чертежа и направлена «к нам» |
Тема:
Явление электромагнитной индукции
Контур
площадью
![]() м2
расположен перпендикулярно к линиям
магнитной индукции. Магнитная индукция
изменяется по закону
м2
расположен перпендикулярно к линиям
магнитной индукции. Магнитная индукция
изменяется по закону
![]()
![]() .
ЭДС индукции, возникающая в контуре,
изменяется по закону …
.
ЭДС индукции, возникающая в контуре,
изменяется по закону …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
В
соответствии с законом Фарадея для
электромагнитной индукции электродвижущая
сила индукции в замкнутом проводящем
контуре численно равна и противоположна
по знаку скорости изменения магнитного
потока сквозь поверхность, ограниченную
этим контуром:
.
Поскольку плоскость контура перпендикулярна
линиям магнитной индукции,
где
S
– площадь контура. Таким образом,
![]() .
.
Тема:
Явление электромагнитной индукции
Сила
тока, протекающего в катушке, изменяется
по закону
![]() .
Если при этом на концах катушки в момент
времени
.
Если при этом на концах катушки в момент
времени
![]() наводится
ЭДС самоиндукции величиной
наводится
ЭДС самоиндукции величиной
![]() ,
то индуктивность катушки (в
,
то индуктивность катушки (в
![]() )
равна …
)
равна …
|
|
|
0,01 |
|
|
|
0,2 |
|
|
|
0,1 |
|
|
|
0,02 |
Решение:
ЭДС
самоиндукции, возникающая в контуре
при изменении в нем силы тока I,
определяется по формуле:
,
где L
–
индуктивность контура. Знак минус в
формуле соответствует правилу Ленца:
индукционный ток направлен так, что
противодействует изменению тока в цепи:
замедляет его возрастание или убывание.
Таким образом, ЭДС самоиндукции равна
![]() .
Следовательно,
.
Следовательно,
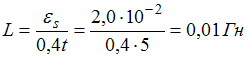 .
.
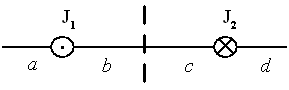
Тема: Магнитостатика
На
рисунке изображены сечения двух
прямолинейных длинных параллельных
проводников с противоположно направленными
токами, причем ![]() .
Индукция
магнитного
поля равна нулю на участке …
.
Индукция
магнитного
поля равна нулю на участке …
|
|
|
а |
|
|
|
b |
|
|
|
c |
|
|
|
d |
Решение:
Линии
магнитной индукции прямолинейных
длинных проводников с токами
![]() и
и
![]() представляют
собой концентрические окружности,
плоскости которых перпендикулярны
проводникам, а центры лежат на их осях.
Направления этих линий определяют
правилом правого винта: направление
вращения винта дает направление силовой
линии магнитной индукции, если
поступательное движение винта совпадает
с направлением тока в проводнике.
Индукция
результирующего
магнитного поля определяется по принципу
суперпозиции
представляют
собой концентрические окружности,
плоскости которых перпендикулярны
проводникам, а центры лежат на их осях.
Направления этих линий определяют
правилом правого винта: направление
вращения винта дает направление силовой
линии магнитной индукции, если
поступательное движение винта совпадает
с направлением тока в проводнике.
Индукция
результирующего
магнитного поля определяется по принципу
суперпозиции
![]() и
равна нулю, если векторы
и
равна нулю, если векторы
![]() и
и
![]() противоположно
направлены и равны по модулю. Это
может быть только в точках интервалов
а
и d.
Поскольку магнитная индукция прямолинейного
длинного проводника с током вычисляется
по формуле
противоположно
направлены и равны по модулю. Это
может быть только в точках интервалов
а
и d.
Поскольку магнитная индукция прямолинейного
длинного проводника с током вычисляется
по формуле
![]() ,
то модули векторов
и
равны,
если
,
так как по условию
.
Следовательно, индукция
результирующего
магнитного поля равна нулю в некоторой
точке интервала а.
,
то модули векторов
и
равны,
если
,
так как по условию
.
Следовательно, индукция
результирующего
магнитного поля равна нулю в некоторой
точке интервала а.
Тема:
Магнитостатика
На рисунке изображены
сечения двух параллельных прямолинейных
длинных проводников с одинаково
направленными токами, причем
:
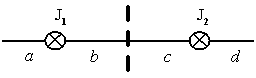 Индукция
результирующего
магнитного поля равна нулю в некоторой
точке интервала …
Индукция
результирующего
магнитного поля равна нулю в некоторой
точке интервала …
|
|
|
b |
|
|
|
a |
|
|
|
c |
|
|
|
d |
Решение: Линии магнитной индукции прямолинейных длинных проводников с токами и представляют собой концентрические окружности, плоскости которых перпендикулярны проводникам, а центры лежат на их осях. Касательные к этим линиям в любой точке совпадают с направлением вектора магнитной индукции . Направления этих линий определяют правилом правого винта: направление вращения винта дает направление силовой линии магнитной индукции, если поступательное движение винта совпадает с направлением тока в проводнике. Индукция результирующего магнитного поля определяется по принципу суперпозиции и равна нулю, если векторы и противоположно направлены и равны по модулю. Это может быть только в точках интервалов b и c. Поскольку магнитная индукция прямолинейного длинного проводника с током вычисляется по формуле , то модули векторов и равны, если , так как по условию . Следовательно, индукция результирующего магнитного поля равна нулю в некоторой точке интервала b.
