
- •Кинематика поступательного и вращательного движения
- •Тема: Кинематика поступательного и вращательного движения
- •Тема: Кинематика поступательного и вращательного движения
- •Тема: Кинематика поступательного и вращательного движения
- •Тема: Кинематика поступательного и вращательного движения
- •Тема: Кинематика поступательного и вращательного движения
- •Тема: Элементы специальной теории относительности
- •Тема: Элементы специальной теории относительности
- •Тема: Элементы специальной теории относительности
- •Тема: Элементы специальной теории относительности
- •Тема: Динамика вращательного движения
- •Тема: Динамика вращательного движения
- •Тема: Динамика вращательного движения
- •Тема: Динамика вращательного движения
- •Тема: Динамика вращательного движения
- •Тема: Законы сохранения в механике
- •Тема: Законы сохранения в механике
- •Тема: Законы сохранения в механике
- •Тема: Законы сохранения в механике
- •Тема: Распределения Максвелла и Больцмана
- •Тема: Распределения Максвелла и Больцмана
- •Тема: Распределения Максвелла и Больцмана
- •Тема: Распределения Максвелла и Больцмана
- •Тема: Распределения Максвелла и Больцмана
- •Тема: Средняя энергия молекул
- •Тема: Средняя энергия молекул
- •Тема: Средняя энергия молекул
- •Тема: Средняя энергия молекул
- •Тема: Средняя энергия молекул
- •Тема: Средняя энергия молекул
- •Тема: Первое начало термодинамики. Работа при изопроцессах
- •Тема: Электростатическое поле в вакууме
- •Тема: Электростатическое поле в вакууме
- •Тема: Электростатическое поле в вакууме
- •Тема: Законы постоянного тока
- •Тема: Законы постоянного тока
- •Тема: Законы постоянного тока
- •Тема: Законы постоянного тока
- •Тема: Магнитостатика
- •Тема: Явление электромагнитной индукции
- •Тема: Магнитостатика
- •Тема: Магнитостатика
- •Тема: Явление электромагнитной индукции
- •Тема: Явление электромагнитной индукции
- •Тема: Уравнения Максвелла
- •Тема: Уравнения Максвелла
- •Тема: Уравнения Максвелла
- •Тема: Сложение гармонических колебаний
- •Тема: Сложение гармонических колебаний
- •Тема: Сложение гармонических колебаний
- •Тема: Свободные и вынужденные колебания
- •Тема: Волны. Уравнение волны
- •Тема: Волны. Уравнение волны
- •Тема: Энергия волны. Перенос энергии волной
- •Тема: Интерференция и дифракция света
- •Тема: Интерференция и дифракция света
- •Тема: Интерференция и дифракция света
- •Тема: Поляризация и дисперсия света
- •Тепловое излучение. Фотоэффект
- •Тема: Тепловое излучение. Фотоэффект
- •Тема: Эффект Комптона. Световое давление
- •Тема: Тепловое излучение. Фотоэффект
- •Тема: Эффект Комптона. Световое давление
- •Тема: Эффект Комптона. Световое давление
- •Тема: Тепловое излучение. Фотоэффект
- •Тема: Спектр атома водорода. Правило отбора
- •Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
- •Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
- •Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
- •Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
- •Тема: Уравнения Шредингера (общие свойства)
- •Тема: Уравнение Шредингера (конкретные ситуации)
- •Тема: Уравнения Шредингера (общие свойства)
- •Тема: Уравнение Шредингера (конкретные ситуации)
- •Тема: Уравнения Шредингера (общие свойства)
- •Тема: Уравнение Шредингера (конкретные ситуации)
- •Тема: Уравнение Шредингера (конкретные ситуации)
- •Тема: Уравнения Шредингера (общие свойства)
Тема: Законы постоянного тока
Через
лампу, подключенную к источнику тока с
ЭДС 8 В и внутренним сопротивлением
1 Ом протекает ток 2 А.
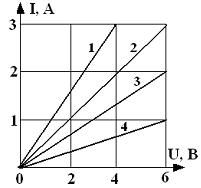
Зависимость тока от приложенного к
лампе напряжения показана на графике
…
|
|
|
3 |
|
|
|
4 |
|
|
|
1 |
|
|
|
2 |
Решение:
Согласно
закону Ома для замкнутой цепи, сила
тока, который протекает по проводнику,
рассчитывается по формуле
![]() ,
где
,
где
![]() –
ЭДС источника тока,
–
ЭДС источника тока,
![]() –
сопротивление проводника (в данном
случае лампы),
–
сопротивление проводника (в данном
случае лампы),
![]() –
внутреннее сопротивление источника
тока. Сопротивление лампы
–
внутреннее сопротивление источника
тока. Сопротивление лампы
![]() .
Из рисунка следует, что сопротивление
лампы
.
Из рисунка следует, что сопротивление
лампы
![]() соответствует
графику 3.
соответствует
графику 3.
Тема: Законы постоянного тока
Напряжение
на концах медного провода диаметром d
и длиной l равно
![]() .
При увеличении напряжения в 4 раза
удельная тепловая мощность тока …
.
При увеличении напряжения в 4 раза
удельная тепловая мощность тока …
|
|
|
увеличится в 16 раз |
|
|
|
увеличится в 4 раза |
|
|
|
не изменится |
|
|
|
уменьшится в 16 раз |
Решение:
Согласно
закону Джоуля – Ленца в дифференциальной
форме,
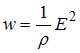 ,
где
,
где
![]() удельная
тепловая мощность тока,
удельная
тепловая мощность тока,
![]() удельное
сопротивление,
удельное
сопротивление,
![]() напряженность
электрического поля в проводнике.
Поскольку
напряженность
электрического поля в проводнике.
Поскольку
![]() ,
напряженность поля также увеличится в
4 раза, следовательно, удельная тепловая
мощность тока увеличится
в 16 раз.
,
напряженность поля также увеличится в
4 раза, следовательно, удельная тепловая
мощность тока увеличится
в 16 раз.
Тема: Законы постоянного тока
Напряжение на концах медного провода диаметром d и длиной l равно . Если взять медный провод диаметром d, но длиной 2l и увеличить напряжение в 4 раза, то среднее время дрейфа электронов от одного конца проводника до другого …
|
|
|
не изменится |
|
|
|
увеличится в 4 раза |
|
|
|
увеличится в 2 раза |
|
|
|
уменьшится в 4 раза |
Решение:
Время,
которое требуется в среднем для того,
чтобы электроны продрейфовали на
расстояние l,
определяется соотношением
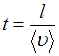 ,
где
,
где
![]() –
средняя скорость упорядоченного движения
(дрейфа) электронов. Формула, связывающая
силу тока со средней скоростью
упорядоченного движения носителей
тока, имеет вид
–
средняя скорость упорядоченного движения
(дрейфа) электронов. Формула, связывающая
силу тока со средней скоростью
упорядоченного движения носителей
тока, имеет вид
![]() ,
где q0
– заряд носителей, в данном случае –
электронов, n
– их концентрация, S
– площадь поперечного сечения проводника.
С учетом закона Ома для участка цепи
,
где q0
– заряд носителей, в данном случае –
электронов, n
– их концентрация, S
– площадь поперечного сечения проводника.
С учетом закона Ома для участка цепи
![]() и
формулы для сопротивления проводника
и
формулы для сопротивления проводника
![]() получаем
выражение для средней скорости
направленного движения электронов
получаем
выражение для средней скорости
направленного движения электронов
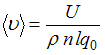 ,
из которого следует, что
не
зависит от диаметра провода. Тогда время
дрейфа
,
из которого следует, что
не
зависит от диаметра провода. Тогда время
дрейфа
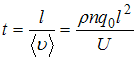 .
Таким образом, если взять медный провод
диаметром d,
но длиной 2l
и увеличить напряжение в 4 раза, то
среднее время дрейфа электронов от
одного конца проводника до другого не
изменится.
.
Таким образом, если взять медный провод
диаметром d,
но длиной 2l
и увеличить напряжение в 4 раза, то
среднее время дрейфа электронов от
одного конца проводника до другого не
изменится.
Тема:
Законы постоянного тока
На
рисунке показана зависимость силы тока
в электрической цепи от времени.
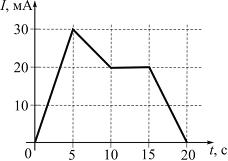 Наименьший
заряд протечет через поперечное сечение
проводника в промежутке времени
________ с.
Наименьший
заряд протечет через поперечное сечение
проводника в промежутке времени
________ с.
|
|
|
15–20 |
|
|
|
0–5 |
|
|
|
5–10 |
|
|
|
10–15 |
Решение:
По
определению сила тока в цепи
![]() .
Отсюда
.
Отсюда
![]() ,
где
,
где
![]() –
заряд, прошедший через
поперечное сечение проводника за
бесконечно малый промежуток времени
–
заряд, прошедший через
поперечное сечение проводника за
бесконечно малый промежуток времени
![]() .
Заряд, прошедший за определенный
промежуток времени, можно определить
по формуле
.
Заряд, прошедший за определенный
промежуток времени, можно определить
по формуле 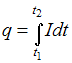 .
Используя геометрический смысл
определенного интеграла, приходим
к выводу, что наименьший заряд протечет
через поперечное сечение проводника
в промежутке времени 15–20 с.
.
Используя геометрический смысл
определенного интеграла, приходим
к выводу, что наименьший заряд протечет
через поперечное сечение проводника
в промежутке времени 15–20 с.
