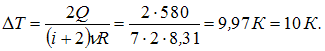Тема: Средняя энергия молекул

Отношение средней кинетической энергии вращательного движения к средней энергии молекулы с жесткой связью 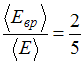.  Это имеет место для …

			водорода
			водяного пара
			гелия
			метана ( )

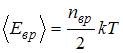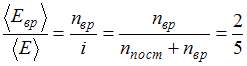Решение: Средняя кинетическая энергия молекулы равна: , где  – постоянная Больцмана, – термодинамическая температура,  – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы: . Средняя энергия вращательного движения . Таким образом, с учетом того что связь атомов в молекуле по условию является жесткой (в этом случае ), отношение . Отсюда , что имеет место для газов с двухатомными и многоатомными линейными молекулами. Следовательно, это – водород.

Тема: Средняя энергия молекул

Средняя кинетическая энергия молекул газа при температуре  зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы. При условии, что имеет место поступательное, вращательное движение молекулы как целого и колебательное движение атомов в молекуле, отношение средней кинетической энергии колебательного движения к полной кинетической энергии молекулы азота ( ) равно …

Решение: Для статистической системы в состоянии термодинамического равновесия на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная , а на каждую колебательную степень –  Средняя кинетическая энергия молекулы равна: .  Здесь – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы: , где  – число степеней свободы поступательного движения, равное 3;  – число степеней свободы вращательного движения, которое может быть равно 0, 2, 3;  – число степеней свободы колебательного движения, минимальное количество которых равно 1. Для молекулярного азота (двухатомной молекулы) ,  и . Следовательно,  Полная средняя кинетическая энергия молекулы азота ( )  равна: , энергия колебательного движения , тогда отношение .

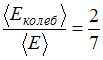Тема: Средняя энергия молекул

При комнатной температуре отношение  молярных теплоемкостей при постоянном давлении и постоянном объеме равно  для …

			кислорода
			водяного пара
			углекислого газа
			гелия

Решение: Из отношения    найдем , . Так как 3 поступательные и 2 вращательные степени свободы имеют двухатомные газы, следовательно, это кислород.

Тема: Средняя энергия молекул В соответствии с законом равномерного распределения энергии по степеням свободы средняя кинетическая энергия молекулы идеального газа при температуре T равна: . Здесь , где ,  и  – число степеней свободы поступательного, вращательного и колебательного движений молекулы соответственно. Для водорода ( ) число i равно …

			7
			5
			3
			6

Решение: Для статистической системы в состоянии термодинамического равновесия на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная , а на каждую колебательную степень – . Средняя кинетическая энергия молекулы равна: . Здесь – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы: , где  – число степеней свободы поступательного движения, равное 3;  – число степеней свободы вращательного движения, которое может быть равно 0, 2, 3;  – число степеней свободы колебательного движения, минимальное количество которых равно 1. Для водорода ( ) (двухатомной молекулы) ,  и . Следовательно,

Тема: Средняя энергия молекул Газ занимает объем 5 л под давлением 2 МПа. При этом кинетическая энергия поступательного движения всех его молекул равна …

Решение: Согласно уравнению кинетической теории для давления идеального газа (основному уравнению МКТ идеальных газов), произведение давления идеального газа и его объема равно двум третям энергии поступательного движения всех его молекул: . Отсюда .

Тема: Средняя энергия молекул Если не учитывать колебательные движения в молекуле водорода при температуре 200 К, то кинетическая энергия в (Дж) всех молекул в 4 г водорода равна …

Решение: Средняя кинетическая энергия одной молекулы равна: , где  – постоянная Больцмана, – термодинамическая температура;  – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы . Молекула водорода  имеет 3 поступательные и 2 вращательные степени свободы, следовательно,  В 4 г водорода содержится  молекул, где масса газа, молярная масса водорода, число Авогадро. Кинетическая энергия всех молекул будет равна:

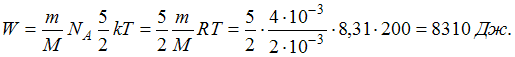
Тема: Первое начало термодинамики. Работа при изопроцессах При изотермическом расширении 1 моля газа его объем увеличился в  раз ( ), работа газа составила 1662 Дж. Тогда температура равна _____ K.

200

Тема: Первое начало термодинамики. Работа при изопроцессах Идеальному трехатомному газу (с нелинейными молекулами) в изобарном процессе подведено количество теплоты . При этом на работу расширения расходуется ________% подводимого количества теплоты. (Считать связь атомов в молекуле жесткой.)

25

Тема: Первое начало термодинамики. Работа при изопроцессах Двум молям водорода сообщили  теплоты при постоянном давлении. При этом его температура повысилась на ______ К. (Считать связь атомов в молекуле жесткой. ) Ответ округлите до целого числа.

10 |

Решение: Согласно первому началу термодинамики, количество теплоты, получаемое газом, равно , где – изменение внутренней энергии, – работа газа. Количество теплоты, сообщаемое газу при постоянном давлении можно представить в виде  Здесь  – число степеней свободы молекул двухатомного газа с жесткой связью атомов в молекуле. Отсюда