Математические модели и их классификация

Требования, предъявляемые к математическим моделям

К математическим моделям предъявляют требования точности, экономичности, универсальности.

Точность математической модели – ее свойство, обращающее степень совпадения, предсказанных с помощью модели значений параметров объекта с истинными значениями этих параметров. Количественная оценка точности модели в большинстве случаев вызывает затруднение по следующим причинам:

1. Реальные объекты, следовательно, и их модели характеризуются не одним, а несколькими параметрами. Отсюда вытекает первоначальный векторный характер оценки, точности и необходимость сопоставления моделей друг с другом.

2. Модели составляют для многократного использования при анализе разных вариантов объекта или даже многих типов объектов определенного класса. Так математическая модель транзистора обычно может применяться при анализе транзисторных схем разных типов с транзисторами разных марок. Поскольку характер проявления тех или иных свойств объекта зависят от особенностей взаимосвязей объекта с внешней средой и другими объектами системы, то и показатели точности отображения этих свойств в модели будут зависеть от конкретных условий функционирования объекта. В результате оценка точным перестает быть однозначной.

3. Истинные значения параметров объекта обычно отождествляют с экспериментально полученными. Однако погрешности эксперимента во многих случаях оказываются соизмеримы с погрешностями математической модели, а иногда и заметно их превышают. Для получения значений, близких к истинным, с помощью более точных математических моделей, чем используемая, требуется наличие такой точности модели, что выполняется не всегда.

Сведение векторной оценки к скалярной обычно осуществляется на основе какой-либо нормы вектора.

Пусть объект характеризуется m выходными параметрами y_j, j=1,2,…,m.

Если в приведенном выше примере выделять такую разность на входе фильтра, причем x_уст делать равной минимально возможному значению выходного сигнала измерительного выпрямителя, получим НИП нестабильности средневыпрямленного значения переменного напряжения.

Для выходного сигнала x_вых рассматриваемого НИП имеем: , (1.2) где - коэффициент преобразования НИП;

- смещение характеристики преобразования НИП.

Наиболее часто требуемая характеристика преобразования НИП должна проходить через начало координат, для чего в (1.2) необходимо иметь x_c=0. Для получения требуемой настройка НИП при номинальных условиях, заключающиеся в устранении смещения x_c и установке требуемого коэффициента преобразования , где - номинальный коэффициент преобразования i-го звена. Следовательно, уравнение номинальной характеристики преобразования имеет вид: (1.3)

При перемещении окружающих условий, например, температура, происходит дополнительное смещение (дрейф) характеристик преобразования НИП, описываемой теперь уравнением (1.2), в котором .

Возникающая при этом абсолютная погрешность преобразования .

Полагая , - относительное изменение k_i, и считая , получаем: (1.4).

Максимальное значение погрешность имеет в случае одинаковых знаков и при .

Обычно НИП характеризуется приведенным значением погрешности, максимальное значение которой с учетом (1.4) определяется выражением: 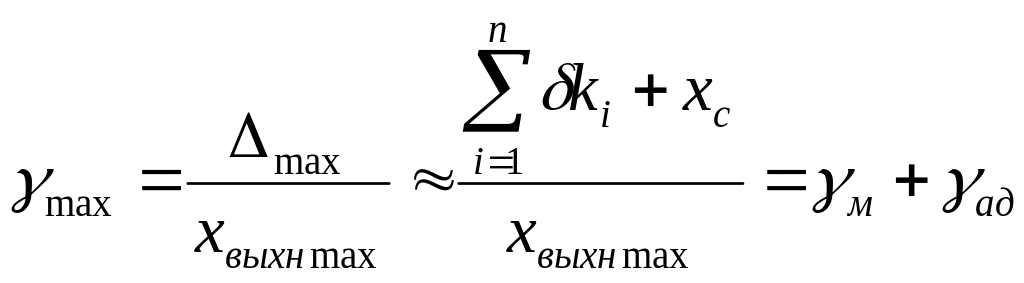, (1.5)

Первое слагаемое (1.5) представляет собой мультипликативную составляющую приведенной погрешности, второе - аддитивную:

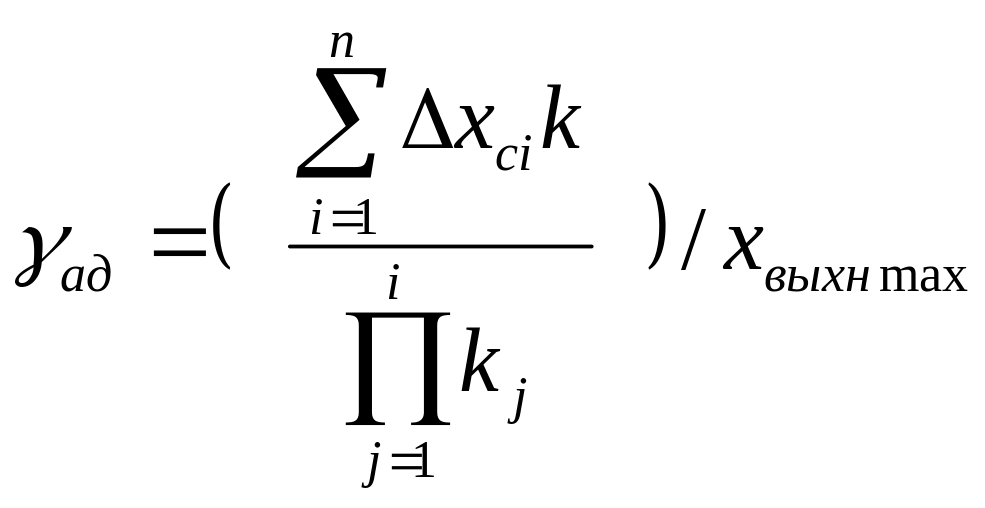; (1.5а)

Таким образом, наибольшая мультипликативная погрешность равна сумме : аддитивная определяется суммой смещений , взятых с соответствующими весовыми коэффициентами. Так, если закон распределения случайных величин нормальный, причем и равны трем средним квадратическим отклонениям, погрешности и с доверительной вероятностью 99,7%, т.е. также соответствующие трем средним квадратическим отклонениям, не превысят следующих значений: ; 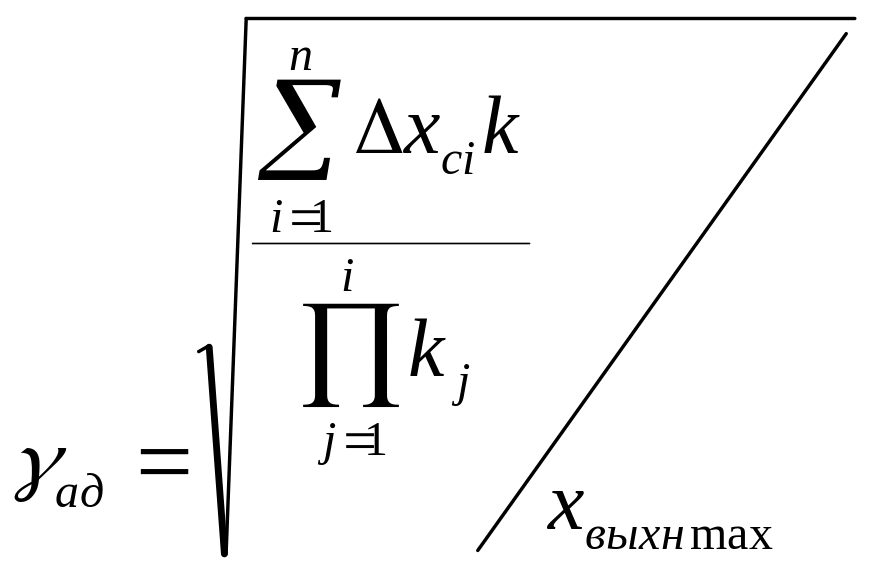(1.5б)

Как видно из (1.5а), (1.5б) относительные изменения коэффициентов и смещения характеристик преобразования в разомкнутых НИП должны быть достаточно малы, что заставляет охватить отдельные звенья таких НИП глубокими ООС, использовать в соответствующих случаях высокостабильные элементы, осуществлять периодическую коррекцию дрейфа и крутизны и т.д.