Вопрос 26. Вынужденное излучение. Мазеры. Лазеры. Накачка метастабильных уровней. Свойства лазерного излучения.

Вынужденное излучение. Атом, находящийся в электромагнитном поле , может с некоторой вероятностью перейти под действием поля в низшее состояние. Электромагнитное поле как бы сваливает атом с возбужденного уровня вниз, на основной или менее возбужденный уровень. Такой переход сопровождается вынужденным излучением вещества, вызванным действием на него электромагнитной волны.

Мазеры

Генераторы когерентного излучения, работающие в диапазоне ультракоротких радиоволн, наз-ся мазерами.

Лазеры. Оптические квантовые генераторы, работающие в оптическом диапазоне, наз –ся лазерами. Важнейшими из существующих типов лазеров являются твердотельные, газовые, полупроводниковые и жидкостные. Более точная классификация учитывает также и методы накачки – оптические, тепловые, химические, электроионизационные. Кроме того, необходимо принимать во внимание и режим генерации – непрерывный и импульсный.

Лазер имеет 3 основных компонента:

1)активную среду, в которой создаются состояния с инверсией населенностей;

2)систему накачки (устройство для создания инверсии в активной среде);

3)оптический резонатор ( устройство, выделяющее в пространство избирательное направление пучка фотонов и формирующее выходящий световой пучок).

Накачка метастабильных уровней.

Процесс создания неравновесного состояния вещества (перевод системы в состояние с инверсией населенностей), необходимое для работы с оптическими квантовыми генераторами , называется накачкой.

Свойства лазерного излучения

1.ВременнАя и пространственная когерентность. Время когерентности составляет с, что соответствует длине когерентности порядка м , т.е. на семь порядков выше, чем для обычных источников света.

2.Строгая монохроматичность ( м).

3.Большая плотность потока энергии. Если, например, рубиновый стержень при накачке получил энергию W=20 Дж и высветился за с, то поток излучения Дж/с = 2* Вт. Фокусируя это излучение на площади 1 , получим плотность потока энергии /S=2* Вт/ = 2* Вт/ .

4.Очень малое угловое расхождение в пучке. Например, при использовании специальной фокусировки луч лазера, направленный с Земли, дал бы на поверхности Луны световое пятно

диаметром примерно 3 км.

К.п.д. лазеров колеблется в широких пределах – от 0,01 до 75%, хотя у большинства лазеро кпд составляет 0,1-1%

27. Фазовое пространство. Функция распределения. Понятие о квантовой статистике Бозе-Эйнштейна и Ферми-Дирака.

Фазовое пространство в классической механике и статистической физике, многомерное пространство всех обобщённых координат q1 и обобщённых импульсов pi (i = 1, 2,..., N) механической системы с N степенями свободы. Таким образом, Ф. п. имеет размерность 2N и может быть описано с помощью ортогональной системы координат с 2N осями соответственно числу обобщённых координат и импульсов. Состояние системы изображается в Ф. п. точкой с координатами qi, pi,..., qN, pn, а изменение состояния системы во времени – движением точки вдоль линии, называемой фазовой траекторией.

Функция распределения, основное понятие статистической физики; характеризует плотность вероятности распределения частиц статистической системы по фазовому пространству (т. е. по координатам (qi и импульсам pi) в классической статистической физике или вероятность распределения по квантовомеханическим состояниям в квантовой статистике.

В классической статистической физике Ф. р. f (p, q, t) определяет вероятность dw = f (p, q, t) dp dq обнаружить систему из N частиц в момент времени t в элементе фазового объёма dpdq = dp1dq1... dpN ´dqN вблизи точки p1, q1,..., pN, qn. Учитывая, что перестановка тождественных (одинаковых) частиц не меняет состояния, следует уменьшить фазовый объём в N! раз; кроме того, удобно перейти к безразмерному элементу (Базового объёма, заменив dpdq на dpdq/N! h3N, где Планка постоянная h определяет минимальный размер ячейки в фазовом пространстве.

Бозо́н — частица с целым значением спина. Бозоны, в отличие от фермионов, подчиняются статистике Бозе — Эйнштейна, которая допускает, чтобы в одном квантовом состоянии могло находиться неограниченное количество одинаковых частиц. Системы из многих бозонов описываются симметричными относительно перестановок частиц волновыми функциями.

Различают элементарные бозоны и составные.

Элементарные бозоны являются квантами калибровочных полей, при помощи которых осуществляется взаимодействие элементарных фермионов (лептонов и кварков) в Стандартной модели.

Фермио́н — по современным научным представлениям: элементарные частицы, из которых складывается вещество. В физике, частица (или квазичастица) с полуцелым значением спина. Фермионы подчиняются статистике Ферми — Дирака: в одном квантовом состоянии может находиться не более одной частицы (принцип Паули). 

Статистика Фе́рми — Дира́ка в статистической физике — квантовая статистика, применяемая к системам тождественных фермионов определяет статистическое распределение фермионов по энергетическим уровням системы, находящейся в термодинамическом равновесии;

В статистике Ферми — Дирака среднее число частиц в состоянии с энергией   есть 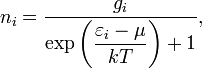где n_i — среднее число частиц в состоянии i, — энергия состояния i,

g_i — кратность вырождениясостояния i (число состояний с энергией  ), μ — химический потенциал (который равен энергии Ферми E_Fпри абсолютном нуле температуры), k — постоянная Больцмана, T — абсолютная температура.

В (идеальном) ферми-газе в пределе низких температур μ = E_F. В этом случае (g_i = 1), функция распределения частиц называется функцией Ферми:

В статистической механике статистика Бо́зе — Эйнште́йна определяет распределение тождественных частиц с нулевым или целочисленным спином по энергетическим уровням в состоянии термодинамического равновесия. Согласно статистике Бозе — Эйнштейна, количество частиц в заданном состоянии i, равняется где  , n_i — количество частиц в состоянии i, g_i — вырождение уровня i, ε_i — энергия состояния i, μ — химпотенциал системы, k — постоянная Больцмана, T — абсолютное значение температуры.

В пределе   статистика Бозе-Эйнштейна переходит в статистику Максвелла — Больцмана, а в пределе   — в распределение Рэлея — Джинса:

28.Колебания кристаллической решетки. Теория Дебая теплоемкости кристаллов. Энергия нулевых колебаний.

Колебания кристаллической решетки

Колебания кристаллической решётки, один из основных видов внутренних движений твёрдого тела, при котором составляющие его частицы (атомы или ионы) колеблются около положений равновесия — узлов кристаллической решётки. Колебания кристаллической решетки., например, в виде стоячих или бегущих звуковых волн возникают всякий раз, когда на кристалл действует внешняя сила, изменяющаяся со временем. Однако и в отсутствие внешних воздействий в кристалле, находящемся в тепловом равновесии с

окружающей средой, устанавливается стационарное состояние колебаний, подобно тому как в газе устанавливается стационарное распределение атомов или молекул по скорости их поступательного движения.

Теория Дебая теплоемкости кристаллов

А.Эйнштейн , приближенно считая, что колебания атомов кристаллической решетки независимы, создал качественную квантовую теорию теплоемкости кристаллич. решетки. Она впоследствии была развита П. Дебаем, который учел, что колебания атомов в кристаллич. решетке не являются независимыми. Рассматривая непрерывный спектр частот осцилляров, П. Дебай показал, что основной вклад в среднюю энергию квантового осциллятора вносят колебания низких частот, соответствующих упругим волнам. Поэтому тепловое возбуждение твердого тела можно описать в виде упругих волн, распространяющихся в кристалле. Согласно корпускулярно- волновому дуализму свойств вещества, упругим волнам в кристалле сопоставляют фононы, обладающие энергией Е=h . Фонон есть квант энергии звуковой волны. Фононы являются квазичастицами – элементарными возбуждениями, ведущими себя подобно микрочастицам.

Энергия кристаллической решетки рассматривается как энергия фононного газа, подчиняющегося статистике Бозе- Эйнштейна ,т..к. фононы являются бозонами ( их спин равен нулю).

Применение статистики Бозе – Эйнштейна к фононному газу – газу из невзаимодействующих бозе – частиц – привело Дебая к количественному выводу, согласно которому при высоких температурах , когда Т>>ТD ,

Теплоемкость твердых тел описывается законом Дюлонга и Пти, а при низких температурах, когда Т<<ТD

- прпорциональна кубу термодинамической температуры:

. В данном случае ТD - характеристическая температура Дебая.

Т.О. теория Дебая объяснила расхождение опытных и теоретических значений теплоемкости твердых тел.

Энергия нулевых колебаний.

Существование минимальной энергии – она называется энергией нулевых колебаний- является типичной для квантовых систем и представляет собой прямое следствие соотношения неопределенностей. Наличие нулевых колебаний означает, что ч – ца не может находиться на дне «потенциальной ямы», причем этот вывод не зависит от ее формы. В самом деле, «падение на дно ямы» связано с обращением в нуль импульса ч – цы,а вместе с тем и его неопределенности. Тогда неопред – сть координаты становится сколь угодно большой, что противоречит пребыванию ч – цы в «потенциальной яме».