Вопрос 22. Атом водорода. Потенциалы возбуждения и ионизации. Квантовые числа. Вырожденные состояния.

Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Ze

(11) где r - расстояние между электроном и ядром, получим уравнение Шредингера в виде

(12) где m масса электрона Е- полная энергия электрона в атоме.

(13)

В теории диф уравнений доказывается, что уравнение (12) имеет решение только при дискретных отрицательных значениях энергии (14)

где n = 1, 2, 3,... главные квантовые числа.

Самый нижний уровень Е1 отвечающей минимальной возможной энергии- основной, все остальные- возбужденные. При Е<0 движение электрона является связанным- он находится внутри гиперболической потенциальной ямы. По мере роста главного квантового числа n энергетические уровни располагаются теснее и при n= при E> 0 соответствует ионизированному атому. Энергия ионизация атома водорода равна На освобождение электрона от связи с атомным ядром, вследствие чего и происходит образование положительного иона, необходимо затратить определенное количество энергии. Энергия, израсходованная на отрыв электрона, называется работой ионизации. Количество энергии, выраженное в электронвольтах, которое необходимо затратить для возбуждения атома или молекулы газа, называется потенциалом возбуждения. Возбужденное состояние атома или молекулы газа является неустойчивым, и электрон может снова возвратиться на стационарную орбиту, а атом или молекула перейдет в нормальное невозбужденное состояние. Энергия возбуждения при этом передается в окружающее пространство в форме светового электромагнитного излучения.

Главное квaнтовое число n определяет общую энергию электрона и степень его удаления от ядра (номер энергетического уровня); оно принимает любые целочисленные значения, начиная с 1 (n = 1, 2, 3, . . .) Момент импульса электрона квантируется

Орбитальное (побочное или азимутальное) квантовое число l определяет форму атомной орбитали. Оно может принимать целочисленные значения от 0 до n-1 (l = 0, 1, 2, 3,..., n-1).

Магнитное квантовое число m определяет ориентацию орбитали в пространстве относительно внешнего магнитного или электрического поля. В квантовом состоянии с заданным значением орбитального квантового числа , магнитное квантовое число может принимать различных значений из ряда.

Вторая часть билета!

Вопрос 23. Ширина спектральных линий. Мультиплетность спектров. Спин электрона. Магнетон Бора.

Мультиплетность спектров: Структура спектра, отражающая расщепление линий на компоненты, называется тонкой структурой. Сложные линии, состоящие из нескольких компонент, получили название мультиплетов. Тонкая структура обнаруживается, кроме щелочных металлов, также и у других элементов, причем число компонент в мультиплете может быть равно 2м, 3м, 4м, 5 ти и тд. В частном случае спектральные линии могут быть одиночными.

Расщепление спектральных линий, обусловлено расщеплением энергетических уровней. Для объяснения расщепления уровней Гаудсмит и Уленбек выдвинули гипотезу о том, что Электрон обладает собственным неуничтожимым механическим моментом импульса, не связанным с движением электрона в пространстве,- спином.

Согласно общим выводам квантовой механики, спин квантуется по закону:

Ls=h , где s – спиновое квантовое число.

Спин электрона- это внутреннее неотъемлемое свойство электрона, подобное его заряду и массе.

Если электрону приписывается собственный механический момент импульса(спин) Ls, то ему соответствует собственный магнитный момент Рms и направленный в противоположную сторону: Рms= Величина . называется гидромагнитным отношением спиновых моментов. Прекция собственного магнитного момента на направление вектора В может принимать только одно из следующих 2х значений: , где h= h/ (2 (h- постоянная Планка), - магнетон Бора, являющийся единицей магнитного момента электрона.

Ширина спектральных линий, интервал частот v (или длин волн l = c/n, с — скорость света), характеризующий спектральные линии в спектрах оптических атомов, молекул и др. квантовых систем. Каждому излучательному квантовому переходу между дискретными уровнями энергии E_k и E_iсоответствует некоторый интервал Dn_ki частот, близких к частоте перехода   (  — Планка постоянная). Значение Dn_ki определяет Ш. с. л. ¾ степень немонохроматичности данной спектральной линии. Контур спектральной линии j(n) [зависимость интенсивности испускания (поглощения) от частоты] обычно имеет максимум при частоте перехода n_ki или вблизи неё (см. рис.); за Ш. с. л. принимают разность частот, которым соответствует уменьшение интенсивности вдвое (её называют иногда полушириной спектральной линии). Если не учитывать Доплера эффект, Ш. с. л. 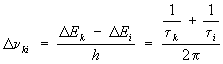Dn_ki определяется суммой ширин уровней энергии E_k и E_i  , т. е. Dn_ki тем больше, чем меньше времена жизни t_k и t_i. Радиационная (естественная) Ш. с. л. соответственно равна: (Dn_ki) _рад = (A_k + A_i)/2p(где A_k и A_i— полные вероятности спонтанных переходов с уровней E_k и E_i на все нижележащие уровни); она очень мала и обычно Ш. с. л. для атомов и молекул определяется в основном уширением их уровней энергии при взаимодействии с окружающими частицами (в газе и плазме — при столкновениях), а также уширением спектральных линий вследствие эффекта Доплера. В зависимости от типа уширения получается симметричный или асимметричный контур спектральных линий (на рис. показан симметричный, т. н. дисперсионный, контур, характерный для радиационного уширения).