Для расчета данной величины приведем таблицу расчетных значений:

Таблица 2. Расчетные данные для нахождения среднеквадратического отклонения.

Номер, n	x	x – x	(x – x)2	Номер, n	x	x – x	(x – x)2
1	9,5	8,075	65,205625	51	0,7	-0,725	0,525625
2	8,5	7,075	50,055625	52	0,7	-0,725	0,525625
3	7,8	6,375	40,640625	53	0,7	-0,725	0,525625
4	6,3	4,875	23,765625	54	0,65	-0,775	0,600625
5	5,2	3,775	14,250625	55	0,65	-0,775	0,600625
6	4,4	2,975	8,850625	56	0,65	-0,775	0,600625
7	4,3	2,875	8,265625	57	0,6	-0,825	0,680625
8	4,3	2,875	8,265625	58	0,6	-0,825	0,680625
9	4	2,575	6,630625	59	0,6	-0,825	0,680625
10	3,5	2,075	4,305625	60	0,6	-0,825	0,680625
11	3,3	1,875	3,515625	61	0,6	-0,825	0,680625
12	3,2	1,775	3,150625	62	0,6	-0,825	0,680625
13	3,1	1,675	2,805625	63	0,6	-0,825	0,680625
14	3,1	1,675	2,805625	64	0,6	-0,825	0,680625
15	3,1	1,675	2,805625	65	0,6	-0,825	0,680625
16	2,5	1,075	1,155625	66	0,55	-0,875	0,765625
17	2,4	0,975	0,950625	67	0,55	-0,875	0,765625
18	2,4	0,975	0,950625	68	0,55	-0,875	0,765625
19	2,1	0,675	0,455625	69	0,55	-0,875	0,765625
20	2	0,575	0,330625	70	0,5	-0,925	0,855625
21	1,9	0,475	0,225625	71	0,5	-0,925	0,855625
22	1,9	0,475	0,225625	72	0,5	-0,925	0,855625
23	1,8	0,375	0,140625	73	0,5	-0,925	0,855625
24	1,8	0,375	0,140625	74	0,5	-0,925	0,855625
25	1,8	0,375	0,140625	75	0,5	-0,925	0,855625
26	1,6	0,175	0,030625	76	0,5	-0,925	0,855625
27	1,2	-0,225	0,050625	77	0,5	-0,925	0,855625
28	1,1	-0,325	0,105625	78	0,5	-0,925	0,855625
29	1	-0,425	0,180625	79	0,5	-0,925	0,855625
30	1	-0,425	0,180625	80	0,5	-0,925	0,855625
31	1	-0,425	0,180625	81	0,5	-0,925	0,855625
32	1	-0,425	0,180625	82	0,5	-0,925	0,855625
33	1	-0,425	0,180625	83	0,45	-0,975	0,950625
34	0,9	-0,525	0,275625	84	0,45	-0,975	0,950625
35	0,9	-0,525	0,275625	85	0,45	-0,975	0,950625
36	0,9	-0,525	0,275625	86	0,45	-0,975	0,950625
37	0,9	-0,525	0,275625	87	0,45	-0,975	0,950625
38	0,9	-0,525	0,275625	88	0,4	-1,025	1,050625
39	0,85	-0,575	0,330625	89	0,4	-1,025	1,050625
40	0,85	-0,575	0,330625	90	0,4	-1,025	1,050625
41	0,85	-0,575	0,330625	91	0,4	-1,025	1,050625
42	0,8	-0,625	0,390625	92	0,4	-1,025	1,050625
43	0,8	-0,625	0,390625	93	0,4	-1,025	1,050625
44	0,8	-0,625	0,390625	94	0,4	-1,025	1,050625
45	0,8	-0,625	0,390625	95	0,4	-1,025	1,050625
46	0,75	-0,675	0,455625	96	0,4	-1,025	1,050625
47	0,7	-0,725	0,525625	97	0,4	-1,025	1,050625
48	0,7	-0,725	0,525625	98	0,4	-1,025	1,050625
49	0,7	-0,725	0,525625	99	0,4	-1,025	1,050625
50	0,7	-0,725	0,525625	100	0,4	-1,025	1,050625
ИТОГО						299,7175

Подставляя в приведенную выше формулу значения, отраженные в таблице, находим среднеквадратическое отклонение:  = 1,731 млрд. рублей. На основе полученных данных о среднеквадратическом отклонении вычислим коэффициент вариации по формуле:

_ = 100%

Получаем, что _ = 121%.

Построим вариационный ряд.

x_max = 9,500 млрд. $,

х_min = 0,400 млрд. $.

Для определения числа групп, на которые будем делить совокупность, воспользуемся формулой Стерджесса:

k=1+3,322 lg100 ≈ 8

Для определения размера интервала используется формула:

h = , R = x_max – x_min,

где R – размах вариации, x_max – максимальное значение признака, х_min – минимальное, n – количество интервалов, на которые разбивается генеральная совокупность..

Таким образом, размах вариации R = 9,5 –0,4 = 9,1 млрд. $.

h=9,1/8≈1,14

Таблица 3. Распределение капитала.

Величина активов, млн. $., x	Кол-во чел, m
0,4 – 1,44	74
1,44 – 2,58	11
2,58 – 3,72	6
3,72 – 4,86	4
4,86 - 6	1
6 – 7,14	1
7,14 – 8,28	1
8,28 – 9,5	2
Итого	100

При значительно разбросе значений можно получить приемлимое распределение, если брать не равные интервалы, а последовательно возрастающие.

Таблица 4

Величина активов, млн. $., x	Кол-во		Середина интервала xi	ximi	Накопленные		Плотность распределения	Доля активов групп лиц в общей сумме активов
	Кол-во чел, mi	% к итогу, wi					Yi=wi/hi
					Частоты, Fi	Частности, pi			Нарастающим итогом, q
А	1	2	3	4	5	6	7	8	9	10
0,3 - 0,4	13	13	0,35	4,55	13	13	130	0,03	0,03	0,0009
0,4 – 0,49	5	5	0,45	2,25	18	18	55,56	0,02	0,05	0,0004
0,5 – 0,59	17	17	0,55	9,35	35	35	188,89	0,07	0,12	0,0049
0,6 – 0,69	12	12	0,65	7,8	47	47	133,33	0,05	0,17	0,0025
0,7 - 0,79	8	8	0,75	6	55	55	88,89	0,04	0,21	0,0016
0,8 - 1	13	13	0,9	11,7	68	68	65	0,08	0,29	0,0064
1,1 - 1,5	6	6	1,3	7,8	74	74	15	0,05	0,34	0,0025
1,6 - 2	7	7	1,8	12,6	81	81	17,5	0,09	0,43	0,0081
2,1 - 2,5	4	4	2,3	9,2	85	85	10	0,06	0,49	0,0036
2,6 - 3	0	0	2,8	0	85	85	0	0	0,49	0
3,1 - 3,5	6	6	3,3	19,8	91	91	15	0,14	0,63	0,0196
3,6 - 4	1	1	3,8	3,8	92	92	2,5	0,03	0,66	0,0009
4,1 - 4,5	3	3	4,3	12,9	95	95	7,5	0,09	0,75	0,0081
4,6 - 9,5	5	5	7	35	100	100	1,02	0,25	1	0,0625
Итого	100	100	-	142,75				1		0,122

Рассчитаем взвешенные величины, то есть величины, рассчитанные с учетом веса (частоты), взятого из приведенного выше интервального ряда.

Формула средней арифметической взвешенной:

 = ,

где x – дискретное значение признака (т.е. среднее значение из интервала, x_i ), m –вес, частота, с которой в интервале встречается признак. Подставив полученные данные в формулу (занесены в таблице), получаем: х = 1,428 млрд. $.

Продолжение таблицы 4.

Величина активов, млрд. $., x	Кол-во чел, mi	Середина интервала xi	ximi	xi 2m	|х – хср |	|x- хср |m
0,3 - 0,4	13	0,35	4,55	1,56	1,078	14,014
0,4 – 0,49	5	0,45	2,25	1	0,978	4,89
0,5 – 0,59	17	0,55	9,35	5,1	0,878	14,926
0,6 – 0,69	12	0,65	7,8	5,04	0,778	9,336
0,7 - 0,79	8	0,75	6	4,48	0,678	5,424
0,8 - 1	13	0,9	11,7	10,53	0,528	6,864
1,1 - 1,5	6	1,3	7,8	10,14	0,128	0,768
1,6 - 2	7	1,8	12,6	22,68	0,372	2,604
2,1 - 2,5	4	2,3	9,2	21,16	0,872	3,488
2,6 - 3	0	2,8	0	0	1,372	0
3,1 - 3,5	6	3,3	19,8	65,34	1,872	11,232
3,6 - 4	1	3,8	3,8	14,44	2,372	2,372
4,1 - 4,5	3	4,3	12,9	55,47	2,872	8,616
4,6 - 9,5	5	7	35	245	5,572	27,86
ИТОГО			142,75	461,94		112,394

Продолжение таблицы 4.

Величина активов, млн. $., x	Кол-во чел, mi	Середина интервала xi	(х - х)2	(х - х)2 m	(х - х)4	(х - х)4 m
0,3 - 0,4	13	0,35	1,16	15,08	1,35	17,55
0,4 – 0,49	5	0,45	0,96	4,8	0,92	4,6
0,5 – 0,59	17	0,55	0,77	13,09	0,59	10,03
0,6 – 0,69	12	0,65	0,61	7,32	0,37	4,44
0,7 - 0,79	8	0,75	0,46	3,68	0,21	1,68
0,8 - 1	13	0,9	0,28	3,64	0,08	1,04
1,1 - 1,5	6	1,3	0,02	0,12	0	0
1,6 - 2	7	1,8	0,14	0,98	0,02	0,14
2,1 - 2,5	4	2,3	0,76	3,04	0,58	2,32
2,6 - 3	0	2,8	1,88	0	3,53	0
3,1 - 3,5	6	3,3	3,5	21	12,25	73,5
3,6 - 4	1	3,8	5,63	5,63	31,7	31,7
4,1 - 4,5	3	4,3	8,25	24,75	68,06	204,18
4,6 - 9,5	5	7	31,05	155,25	964,1	4820,5
ИТОГО			55,47	258,38	1083,76	5171,68

Мода – значение признака, которое наиболее часто встречается в вариационном ряду. Для непрерывного (недискретного) ряда применяется формула:

= ,

где

x_k-1 – нижняя граница модального интервала,

h_k – длина модального интервала,

m_k-1, m_k, m_k+1 – частота интервала, соответственно предшествующему модальному, модального и следующего за модальным.

М_o = 0,564 млрд. $.

Медианой называют такое значение признака, которое приходится на середину ранжированного ряда. Таким образом, в ранжированном ряду распределения одна половина ряда имеет значения признака больше медианы, лругая – меньше медианы.

, , где

X_k – нижняя граница медианного интервала,

h_k – длина медианного интервала,

N_Me – номер медианного интервала,

F_k-1 – накопленная частота интервала, предшествующему медианному,

m_k – частота медианного интервала.

N_Me = 100/2 = 50.

M_e = 0,733 млрд. $.

Показатель дисперсии.

. (*)

Дисперсия – средняя величина квадратов отклонений. В данном случае варианты признака выражены в первой степени, значит, и мера их вариации также должна быть взята в первой степени. Для этого достаточно извлечь из дисперсии корень второй степени, тогда мы найдем среднее квадратическое отклонение. Таким образом, среднее квадратическое отклонение имеет вид:

_.

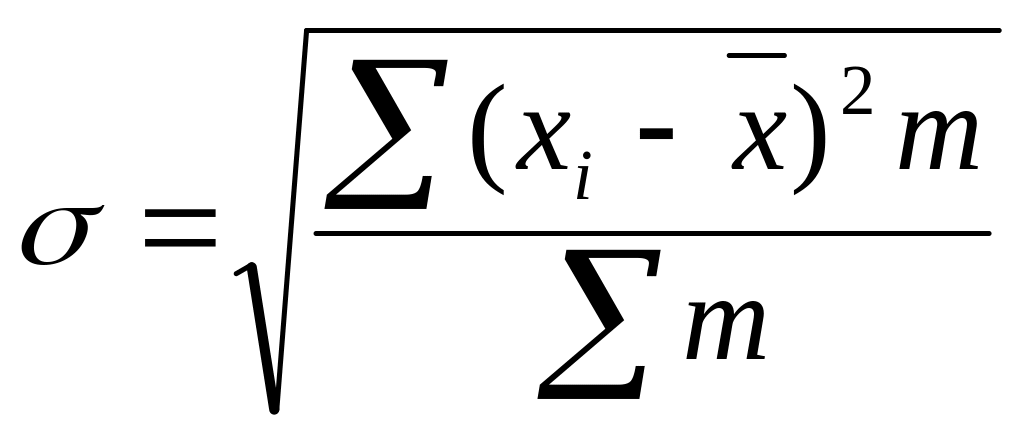Найдем указанные выше величины. Расчетные данные для них указаны в таблице 4. Подставляя их, получаем: ² = 2,583.

σ=1,607 млрд. $

Проверим правило сложения дисперсий.

, где

Дополним Таблицу 4 данными:

Разобъем условно наш ряд на 3 группы и найдем дисперсию для каждой группы по формуле (*):

Величина активов, млн. $., x	Кол-во чел, mi	Середина интервала xi	ximi	х	(х - х)2 m	σ2
0,3 - 0,4	13	0,35	4,55	0,47	0,187	0,0085
0,4 – 0,49	5	0,45	2,25		0,002
0,5 – 0,59	17	0,55	9,35		0,109
ИТОГО	35	1,35	16,15		0,298
0,6 – 0,69	12	0,65	7,8	0,77	0,173	0,012
0,7 - 0,79	8	0,75	6		0,003
0,8 - 1	13	0,9	11,7		0,22
ИТОГО	33	2,3	25,5		0,396
1,1 - 1,5	6	1,3	7,8	3,16	20,758	3,588
1,6 - 2	7	1,8	12,6		12,947
2,1 - 2,5	4	2,3	9,2		2,958
2,6 - 3	0	2,8	0		0
3,1 - 3,5	6	3,3	19,8		0,118
3,6 - 4	1	3,8	3,8		0,41
4,1 - 4,5	3	4,3	12,9		3,899
4,6 - 9,5	5	7	35		73,728
ИТОГО	32	26,6	101,1		114,818

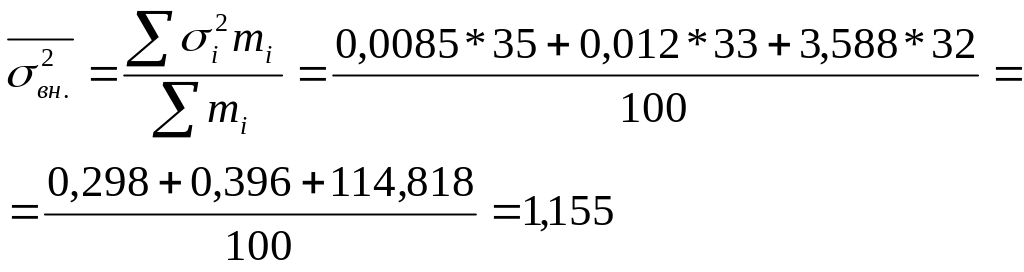
Найдем межгрупповое значение. Х_{ср. общ}=1,428 млрд. $.

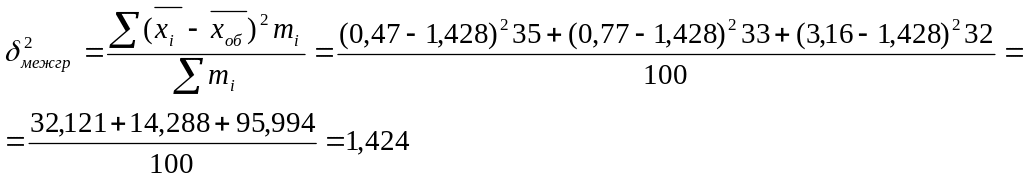
Т. о.

2,583=1,155+1,424

Асимметрия и эксцесс.

Асимметрия показывает степень “скошенности распределения”. Для ее нахождения можно пойти разным путем. Приблизительнор ассимметрию можно вычислить по формулам:

0,54

В данном случае асимметрия заметная и скошенность правосторонняя.

Вариация нормального распределения.

112,53%

Найдем центральный момент четвертого порядка:

А так же нормированный момент четвертого порядка

,

⁴ = 6,671. Следовательно, r₄ = 7,753.

Эксцесс – показатель отклонения распределения от нормального распределения. Наиболее точно он вычисляется по формуле:

, где

₄ – центральный момент 4ого порядка. Расчетные данные занесены в таблицу 4, а Следовательно, получаем:

Е_s =7,753-3=4,753.

Так как Е_s > 3 (3 – величина при нормальном распределении), то наблюдается высоковершинное (островершинное) распределение. Для наглядности сделанных выводов отразим распределение на графике. Так как мы имеем интервальный вариационный ряд, то строим гистограмму и условный полигон.

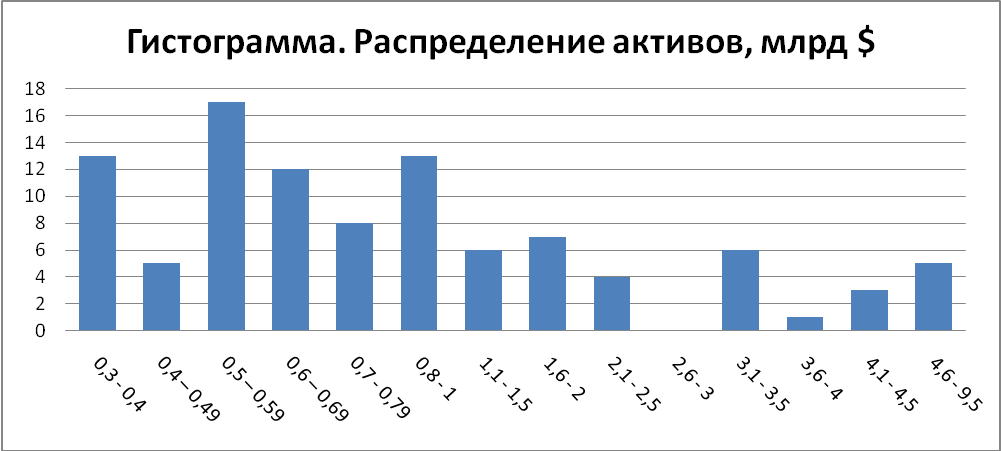
Путем нахождения серединных значений относительно оси OX на каждом секторе гистограммы получаем условный полигон: