Организация данной работы
В главе 2 мы обеспечим необходимый базис, в общих чертах характеризующий LDPC коды, алгоритмы их декодирования и существующие методы анализа этих алгоритмов декодирования.
В главе 3 мы ознакомимся с LDPC декодированием с использованием алгоритмов двоичной передачи сообщений. Мы отслеживаем сообщение об ошибочной скорости, чтобы проанализировать декодер и изобразить EXIT диаграммы, основанные на сообщениях об ошибочной скорости. Также доказано, что алгоритм В Галлагера является, возможно, лучшим бинарным алгоритмом передачи сообщений. Мы используем EXIT диаграммы для разработки неравномерных LDPC кодов и, для того чтобы показать, что процесс кодирования может быть позиционирован в качестве линейного программирования.
В главе 4 мы продолжим анализ главы 3. Опять же, мы используем EXIT диаграммы, основанные на сообщениях об ошибочной скорости, и покажем, как могут быть получены точные EXIT диаграммы. В то время как предыдущие работы по анализу LDPC кодов в AWGN каналах использовали наработки Гаусса для сообщений [24], мы избегаем предположений Гаусса о выходах проверочных узлов, которые на самом деле являются плохими предположениями. Мы называем наш метод «наполовину Гаусса», в отличие от «полного» метода Гаусса, который принимает все гауссовы сообщения. Мы показываем, что очень точный анализ и кодирование LDPC кодов можно осуществить с помощью приближения метода Гаусса. Опять же, мы используем EXIT диаграммы, чтобы уменьшить методику расчета неравномерных LDPC кодов до линейного программирования. Мы также дадим несколько советов по кодированию таких кодов. По сравнению с кодами, кодированными с помощью анализа плотности эволюции, наши коды будут выполнены всего лишь на несколько сотых долей дБ хуже.
В главе 5 мы рассмотрим класс алгоритмов декодирования, для которых анализ EXIT диаграмм декодера является точным (или имеет хорошее приближение). Мы рассматриваем общий случай кодирования кодов для желаемого поведения конвергенции и обеспечиваем необходимые и достаточные условия, для того чтобы были EXIT диаграммы удовлетворяли условию максимальной скорости LDPC кодов. Наши результаты обобщают некоторые из существующих результатов ВЕС.
В
главе 6 мы применяем неравномерные
LDPC коды для разработки
многоуровневых схем кодирования с
последующим их применением в дискретных
мульти тональных системах (DMT).
Мы используем комбинированную маркировку
Грея/Ангербёка для QAM.
Биты, маркированные по Грею, защищены,
благодаря неравномерным
LDPC кодам, в то время как
другие биты защищаются с помощью высокой
скорости кода Рида-Соломона с жёстким
решением декодирования (или остаются
не кодированными). Скорость LDPC
кодов выбирается на основе анализа
пропускной способности канала. Затем
мы применяем эту схему кодирования для
ансамбля частотно-селективных каналов
с гауссовским шумом. Эта схема кодирования
обеспечивает эффективное кодирование
с приростом более чем на 7,5 дБ при
вероятности ошибки
,
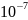которая представляет собой разрыв в
размере примерно 2,3 дБ от предела Шеннона
при передаче по каналу связи с аддитивным
гауссовским шумом. Этот интервал может
быть уменьшен до 0,8-1,2 дБ.
В главе 7 мы рассматриваем декодирование методом переключения передач, в котором итерационный декодер может выбирать правила декодирования среди групп алгоритмов декодирования на каждой итерации. Сначала покажем, что при правильном выборе алгоритма на каждой итерации задержка декодирования может существенно снижаться. Мы покажем, что задача нахождения декодера с оптимальным переключением передач (минимальной задержкой декодирования) может быть позиционирована в качестве динамической программы. Затем мы предложим конструкцию канала связи и оптимизируем декодер с методом переключения передач для достижения минимальной стоимости оборудования вместо минимальной задержки.
В главе 8 мы предоставим краткий обзор данной работы и некоторые предложения для будущих работ.