
- •Глава 1. Введение
- •Коды, определенные на графах
- •Краткая история графических кодов
- •Обзор главной темы
- •Главная тема данной работы
- •Организация данной работы
- •Глава 2. Ldpc коды и их анализ
- •2.1 Графические модели и декодирование методом передачи сообщений
- •2.2 Ldpc коды: структура
- •2.3 Ldpc коды: декодирование
- •2.3.1 Алгоритм sum-product
Краткая история графических кодов
Интересно, что графическое понимание этих кодов сформировалось за долго до того, как их назвали “графическими”. Более того, это понимание помогло теоретикам кодирования в анализе этих кодов и разработке алгоритмов декодирования, они также узнали, как создавать свои коды, чтобы извлечь наибольшую выгоду из данного алгоритма декодирования.
Графическое понимание кодов началось с графов Таннера для линейных кодов [4]. Позже Виберг обнаружил, что турбо декодер также может быть представлен графически [5]. Вскоре после этого открытия, как в [6] и [7], было показано, что алгоритм турбо декодирования представляет собой частный случай общих байесовских сетей [8].
Параллельно с исследованиями турбо кодов, в 1996 году МакКей и Нил [9], а также Сипсер и Шпильман в [10] обнаружили вновь давно забытый класс кодов, а именно LDPC коды. Этот класс кодов был первоначально предложен в 1962 году Галлагером[11], но считался слишком сложными в момент их открытия.
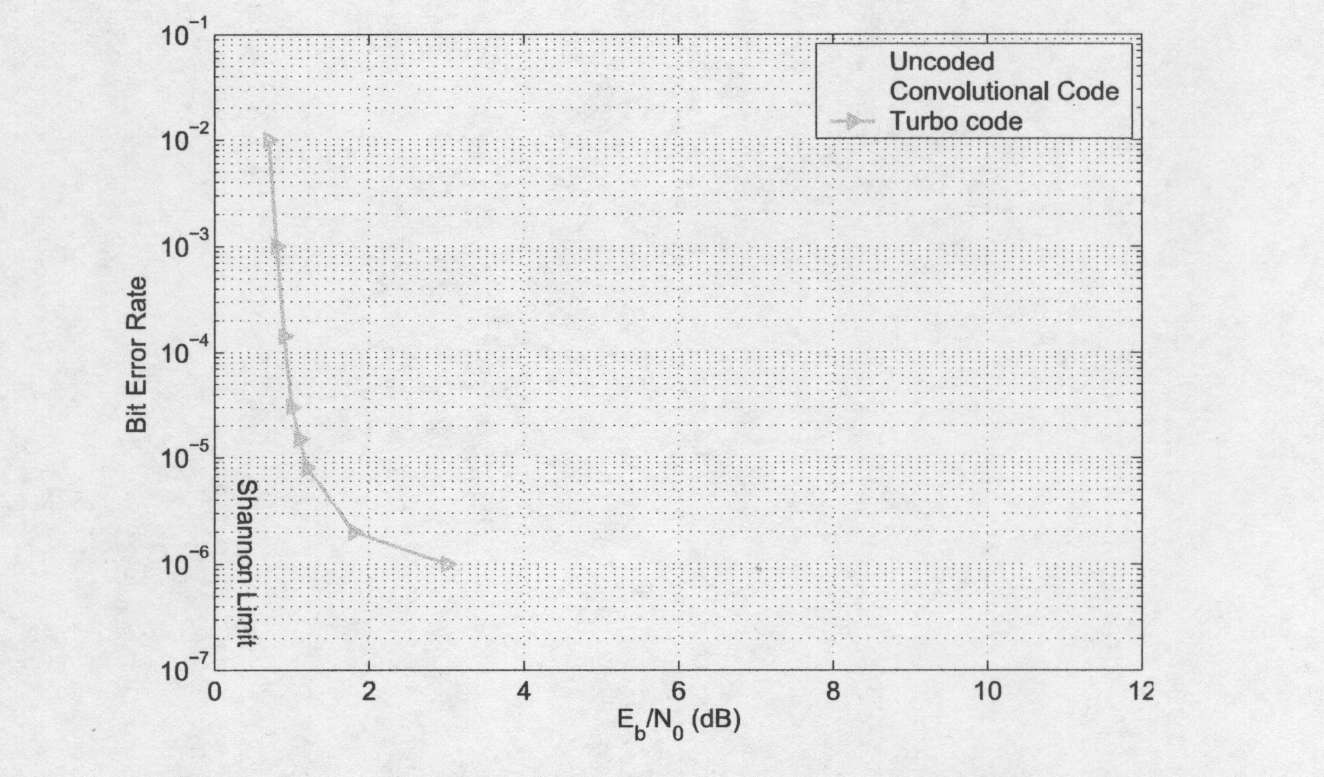
LDPC коды из-за малой вероятности ошибочного декодирования привлекли большое внимание к себе. Например, при передаче по каналу связи с аддитивным гауссовским шумом они могут быть кодированы так, что их вероятность ошибочного декодирования будет отличаться на несколько сотых долей дБ от предела Шеннона. Еще одной особенностью LDPC кодов является их простое графическое представление, основанное на представлении Таннера линейных кодов [4].
Эта простая конструкция позволяет производить точный асимптотический анализ LDPC кодов [12,13], а также кодировать неравномерные LDPC коды, оптимизированные под определенные ограничения.
С открытием LDPC кодов было проделано много научно-исследовательской деятельности и совершенствований технологий в области кодов, определённых на графах. Несомненно, что исследование LDPC кодов сыграло и продолжает играть главную роль в этой области, так как многие из новых классов кодов, которые определяются на графах, подвергаются влиянию структурой LDPC кодов. Примеры включают в себя повтор с накоплением (RA) коды [14], преобразование кодов Люби [15] и каскадных древовидных кодов[16]. Некоторые из ключевых усовершенствований в области графических кодов и их значения приведены ниже.
•Неравномерные LDPC коды: Как показано в [17], неравномерные LDPC коды могут существенно превосходить обычные LDPC коды по ряду показателей. Все LDPC коды, которые могут приблизиться к пределу Шеннона на различных каналах, являются неравномерными LDPC кодами. Открытие неравномерных LDPC кодов повлияло на рассмотрение неравномерных структур других кодов, определенных на графах, таких как неравномерные турбо коды [18] и неравномерные RA коды[19].
•Повторяющиеся коды с накоплением: Одной из проблем LDPC кодов является сложность их кодирования. Люди рассматривали различные способы добавления структур в LDPC коды, чтобы сделать процесс кодирования менее сложным. Одним из лучших решений являются RA коды [14], которые, в отличие от LDPC кодов, имеют несколько иную структуру и меньшие потери производительности. Декодирующая сложность RA кодов растет линейно с длиной блока.
•Возможность LDPC кодов достигать пропускной способности ВЕС канала: Шокроллахи нашёл семейство неравномерных LDPC кодов, которые могли бы достичь пропускной способности ВЕС канала[20,21].
•Плотность эволюции анализа LDPC кодов: точный асимптотический анализ LDPC кодов в рамках различных схем декодирования стал возможным [13]. Идея состоит в том, чтобы проследить плотность эволюции сообщений в декодере. С помощью этого анализа кодирование хороших неравномерных LDPC кодов, которое уже было изучено для ВЕС канала, стало возможным и для других типов каналов.
•Гауссовский анализа турбо кодов и LDPC кодов [22-24]: Из-за сложности вычисления плотности эволюции, аппроксимации плотности эволюции привлекают многих исследователей. В частности, аппроксимация истинной плотности сообщений гауссовской плотностью оказалась очень эффективной.
•Схема анализа внешней передачи информации (EXIT): EXIT анализ схемы [25] похож на плотность эволюции, за исключением того, что он следует за эволюцией одного параметра, который представляет плотность сообщений. Эта эволюция может быть визуализирована в графе, называемом EXIT схемой. EXIT схемы стали очень популярными, поскольку они обеспечивают глубокое понимание поведения итерационного декодера.
•Преобразование Люби (LT коды) [15]: Идея таких кодов - одно из последних изобретений в области теории кодирования. Такие коды полезны, когда у нас есть радиовещательный передатчик, чей канал для каждого приемника отличается от другого. В таких случаях не ясно, какой уровень кода должен быть использован для защиты данных. LT коды являются кодами, решающими эту проблему. Чтобы быть более конкретным, каждый получатель получает различные скорости передачи данных в зависимости от состояния канала.
Исследования в области графических кодов по-прежнему очень активны и многие открытые вопросы всё ещё остаются в стадии изучения.
