2. Аппроксимация функций
2.1. Основные сведения
Определение.
Величина
называется функцией
переменной величины
,
если каждому из тех значений, которые
может принимать
,
поставлено в соответствии по определенному
закону одно или несколько значений
.
При этом переменная величина
называется аргументом.
Аргумент всегда переменная величина,
функция, как правило, тоже.
Говорят также: величина зависит от ; сообразно с этим аргумент называют независимой переменной, функцию – зависимой.
Тот факт, что есть функция от выражают в записи так
,
(2.1)
где -
-
обозначен закон соответствия между
и
.
(функциональная зависимость).
Известно три способа задания функциональной зависимости:
1. аналитический;
2. графический;
3. табличный.
Аналитический способ состоит в указании функции одной или несколькими математическими формулами.
Преимущества:
возможность получения значения для любого фиксированного аргумента с любой точностью и с наименьшими затратами по времени (так как этот способ прямо указывает действия и последовательность их выполнения над независимой переменной для получения соответствующего значения величины ).
Недостатки:
1) на практике часто неизвестна аналитическая формула
2) в некоторых случаях, если известна, то настолько громоздка (содержит трудно вычисляемые выражения, сложные интегралы и т.п.), что ее использование в практических расчетах затруднительно
3) не наглядность с точки зрения поведения функциональной зависимости.
Графический способ состоит в проведении линии (графика) в декартовой системе координат, у которой абсциссы изображают значения аргумента, а ординаты – соответствующие значения функции.
Достоинства:
1) легкость обозрения картинки в целом
2) непрерывность изменения аргумента.
Недостатки:
Ограниченная степень точности, что приводит к утомительности прочитывания значений функции с максимально возможной точностью.
Табличный способ заключается в том, что для избранных значений аргумента указываются соответствующие значения с определенной степенью точности.
Достоинства:
Он сразу дает числовые значения функции для табличного значения аргумента.
Недостатки:
1) Таблица трудно обозрима в целом
2) Она часто не содержит всех необходимых значений аргумента, а для получения этих значений могут потребоваться либо очень сложные расчеты либо проведение дорогостоящих экспериментов.
Задача аппроксимации
функции в
вычислительной математике позволяет
приближенно вычислить значение функции
при любом значении аргумента (из некоторой
области) с наименьшими затратами времени
и средств, если функция задана таблично,
т.е. когда аналитическая функциональная
зависимость неизвестна либо очень
громоздка. И сводится к замене
(аппроксимации) данной функций
приближенной функцией
так, чтобы отклонение (в некотором
смысле)
от
в заданной области было наименьшим.
Функция
при этом называется аппроксимирующей.
На практике в качестве
чаще всего рассматривают многочлен
(2.2)
Таким образом
задача аппроксимации функции сводится
к подбору коэффициентов
,
,
чтобы достичь наименьшего отклонения
многочлена функции
что касается самого понятия «малое
отклонение», то оно уточняется при
рассмотрении конкретных способов
аппроксимации.
Если приближение
строится на заданном дискретном множестве
точек
,
то аппроксимация называется точечной.
К ней относятся, например, интерполирование,
среднеквадратичное приближение. При
построении приближения на непрерывном
множестве точек, например, не отрезке
,
аппроксимация называется непрерывной
(или интегральной).
Интерполирование
Один из основных
типов точечной аппроксимации. Оно
состоит в следующем: для данной табличной
функции
строим многочлен (2.2), принимающий в
заданных точках
те же значения
,
что и функция
,
т.е.
,
(2.3)
при этом, среди
нет одинаковых, т.е.
при
.
Точки называются узлами интерполирования, а многочлен - интерполирующим многочленом.
Таким образом, близость интерполирующего многочлена к заданной функции состоит в том, что их значения совпадают на заданной системе точек.
Максимальная
степень интерполяционного многочлена
.
В этом случае говорят о глобальной
интерполяции,
поскольку один многочлен
(2.4)
используется для интерполяции функции на всем рассматриваемом интервале изменения аргумента .
Интерполяционные многочлены могут строиться отдельно для разных частей рассматриваемого интервала. В этом случае имеет кусочную (или локальную) интерполяцию.
Как правило, интерполяционные многочлены используются для аппроксимации функции в промежуточных точках между крайними узлами интерполяции.
однако иногда они
используются и для приближенного
вычисления функции вне рассматриваемого
отрезка
или
.
Это приближение называется экстраполяцией.
Линейная
интерполяция
– простейший и часто используемый вид
локальной интерполяции. Она состоит в
том, что заданные точки
соединяют прямолинейными отрезками и
функция
приближается ломаной с вершинами в
данных точках.
Уравнения каждого
отрезка ломаной в общем случае разные,
так как имеется n
интервалов
,
то для каждого из них в качестве уравнения
интерполяционного многочлена используется
уравнение многочлена первой степени
(2.5)
В частности для
і-го
интервала
по (2.3) имеем
отсюда
(2.5)
или используя уравнение прямой, проходящей через 2 точки
Следовательно, при использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение аргумента , а затем подставить его (границы интервала) в формулу (2.5).
Квадратичная
(параболическая) интерполяция
– в качестве интерполяционной функции
на отрезке
принимается квадратный трехчлен
(2.6)
Уравнение (2.6) содержит 3 неизвестных коэффициента, для определения которых необходимы 3 уравнения по (2.3) имеем
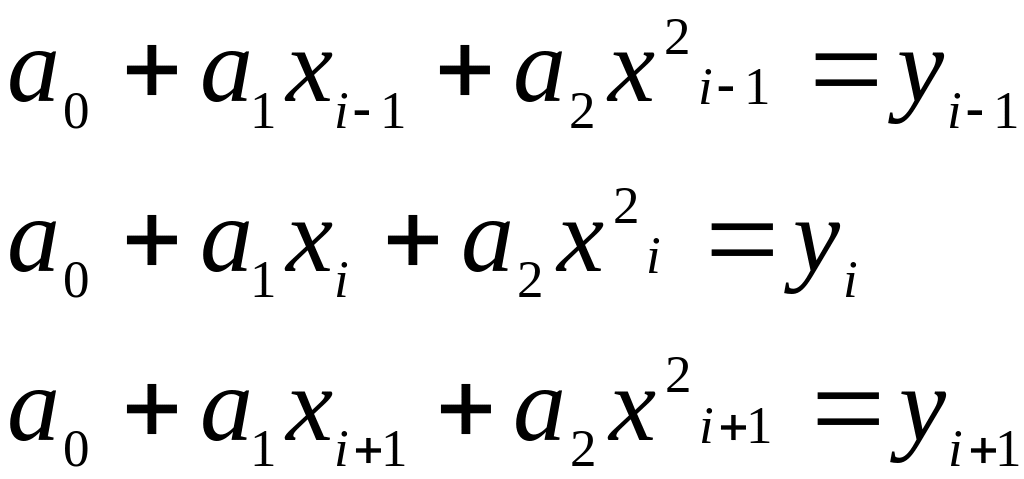
Интерполяция для
любой точки
проводится по 3-м ближайшим к ней углам.