Понимание чужого сознания

Чжуан-цзы и его друг Ши прогуливались по мосту через реку Хао. Чжуан сказал: «Как весело резвятся эти рыбы в воде. Вот радость рыб.».

Ши ответил: «Ты не рыба, откуда тебе знать в чем ее радость?»

Ч. сказал: «Ты не я, откуда тебе знать, что я не знаю в чем радость рыб?»

Ши ответил: «Я не ты и конечно не знаю того, что ты знаешь. Однако и ты не рыба и, безусловно, не можешь знать в чем радость рыб.»

Ч. сказал: «Вернемся к началу нашего разговора, ты спросил меня, откуда я знаю в чем радость рыб, значит, ты уже знал это и, поэтому, спросил, а я знал это, стоя здесь у реки Хао.»

Вопрос: знаете ли вы в чем истина всех вещей?

Ответ: как я могу знать это?

Вопрос: знаете ли вы того, чего не знаете?

Ответ: как я могу это знать?

Вопрос: стало быть, никто ничего не знает?

Ответ: как я могу это знать, но все же попробую рассказать: «как знать, что то, что называется знанием, не является незнанием и как знать, что то, что я называю незнанием, не называется знанием?»

37. Логические и семантические парадоксы. Рациональное мышление и чувственные данные.

Проблема соотношения мышления чувств.

Еще древние греки заметили трудности описания мира рациональным образом. Так Парменид указывал на сильное различие между подлинной истиной, являющейся продуктом рационального освоения действительности, и мнением, основанном на чувственном познании. Чувственные данные дают нам образ лишь кажущегося состояния вещей. С помощью чувственного познания нельзя постичь подлинную сущность вещей. Известна апория Ахиллес-черепаха, в которой Ахиллес должен пройти за конечное время бесконечное число отрезков. Все логические парадоксы имеют общее свойство, которые можно определить, как самоприменение или самоотносимость. Т.е. сущность, о которой идет речь, определяется или характеризуется посредством некоторой совокупности, которой она сама принадлежит.

Ярким примером логического научного вывода, который противоречит обыденным чувственным представлениям, является вывод о свойствах объектов в n-мерном пространстве.

Рассмотрим на плоскости квадрат со стороной 2. n=2. О(0;0), углы (2, 2). По углам впишем окружности радиусом 1, их центры (1,1). Центр окружности: . d={расстояние до ближайшей окружности}=

Теперь рассмотрим куб. n=3. .

Рассмотрим n-мерное пространство, в нем рассмотрим n-мерный куб со стороной 4, по углам которого описано единичной сферы. Определим радиус сферы, который касается всех этих сфер, получаем: .

При n=10 это выражение r_n>2, т.е. вписанная по построению в n-мерный куб сфера выходит за его границы.

Маленькая сфера выходит за размеры куба. Можно показать, что при n→∞ объем n-мерного куба будет намного меньше, чем объем n-мерной сферы.

Вывод: Рассуждения, которые подтверждены данными науки, противоречат обыденным представлениям о метрических соотношениях объектов. Наши макропредставления неприемлемы к n-мерному пространству.

38. Формальные системы.Логика высказываний..

Формальные системы создаются для описания в форме символьных выражений рассуждений об элементах некоторой предмет области. Все эти рассуждения выполняются согласно определённым правилам. Формальная система содержит:

1. Алфавит символов;

2. Правила построения правильных формул или допустимых выражений языка (ПППФ);

3. Логические аксиомы и правила вывода новых выражений из уже имеющихся.

Логика высказываний (пропозициональная логика) и логика предикатов первого и более высокого порядка (они были созданы математиками и логиками) для проверки непротиворечивости математических теорий и контроля правильности доказательств.

* Эта логика имеет дело с предложениями естественного языка

* Каждому высказыванию пытаются приписать истину или ложь.

* Не все предложения ЕЯ могут иметь значения ИСТИНА или ЛОЖЬ (например, «Я лжец»).

Пример Журдена:

На одной стороне карточки написано: «Предложение на другой стороне карточки истинно», а на другой стороне написано: «Предложение на другой стороне карточки ложно».

1) алфавит символов для логики высказываний:

- латинские буквы, которые обозначают истинность или ложность предложения (логического высказывания)

- доказательно используют логические связки: &, ^, →, ¬

- служебные символы, скобки

2) ПППФ

a, b, c - правильные формулы

a&b, a^b, ¬a … правильные формулы

3) ПЛВ

Иногда правило логического вывода выстроено человеческим мышлением, отражающим причинность: a, b → b |- b.

Если наблюдаем А и В следует за А, то наблюдаем А.

39. Коэффициенты конкордации для оценки согласованности экспертов.

Коэффициент конкордации позволяет ответить на вопрос — насколько коррелированны, неслучайны ранжировки каждого из экспертов и насколько они согласованы, а значит — насколько можно доверять результирующим рангам

1) Вычисляем среднее значение суммы рангов (D). Для n факторов и m экспертов получим D = m*(n+1) / 2;

2) Вычисляем отклонение суммы рангов, указанных экспертами, от среднего значения такой суммы (D);

3) Вычисляем сумму квадратов отклонений (S);

4) Вычисляем коэффициент координации R_k = 12*S / (m² * (n³ - n)). Чем ближе вычисленное значение к 1, тем согласованнее мнение экспертов.

Значимость этого критерия α определяем по тиблице хи-квадрат, где χ²=12*S / (m * (n³ - n)), а число степеней свободы = n – 1. Получаем, что мнения экспертов согласовано с вероятностью ошибки α

40. Метод GPS(всеобщий рещатель задач).(самостоятельно)

GPS (General Problems Solver). Авторы - Ньюэл и Саймон.

В основу программы положены 2 основных принципа:

1) Анализ цели и средства.

2) Рекурсивное решение задач.

Задачи, решаемые методом GPS, всегда представляются в следующем виде: исходный объект, конечный объект, множество операторов. Операторы позволяют осуществлять преобразования над объектами и благодаря этому дают возможность постепенно достичь конечного объекта, который и является целью всей работы.

В соответствии с методом редукции поставленную задачу всегда разбивается на более простые подзадачи. Чтобы осуществить разбиение адекватным способом, используются различия, существующие между обрабатываемым объектом и объектом, который мы хотим получить.

Различием между двумя объектами считается любое свойство, присутствующее в одном из них и отсутствующее полностью или частично в другом.

Метод GPS выбирает только те операции, которые могут уменьшить различия, отмеченные на данном этапе поиска.

GPS различает три главные цели:

1. Т(х, у) Преобразовать объект х в объект у

2. С(О, D, х, у) Найти оператор О, который может уменьшить различие D между объектами х и у

3. А(О, х) Применить оператор О к объекту х

Существует разбиение исходной задачи на подзадачи. Программа позволяет решать следующие проблемы:

1) Символьное вычисление интегралов.

2) Задачи логического вывода.

3) Решение игровых задач двух игроков с противоположными целями.

4) Грамматический разбор предложений.

Таким образом, все задачи в исходный момент ориентированы на цель Т (исходный объект, конечный объект).

Кроме того, задана таблица зависимостей, в которой указаны операторы, пригодные для уменьшения каждого типа различий. В соответствии с методами решения и в зависимости от характера исходного объекта и первой цели согласно методу GPS подыскиваем одну или несколько целей. В свою очередь благодаря действию подходящих операторов эти цели раскрываются до тех пор, пока не будет получен конечный объект и пока остаются не полностью раскрытые объекты.

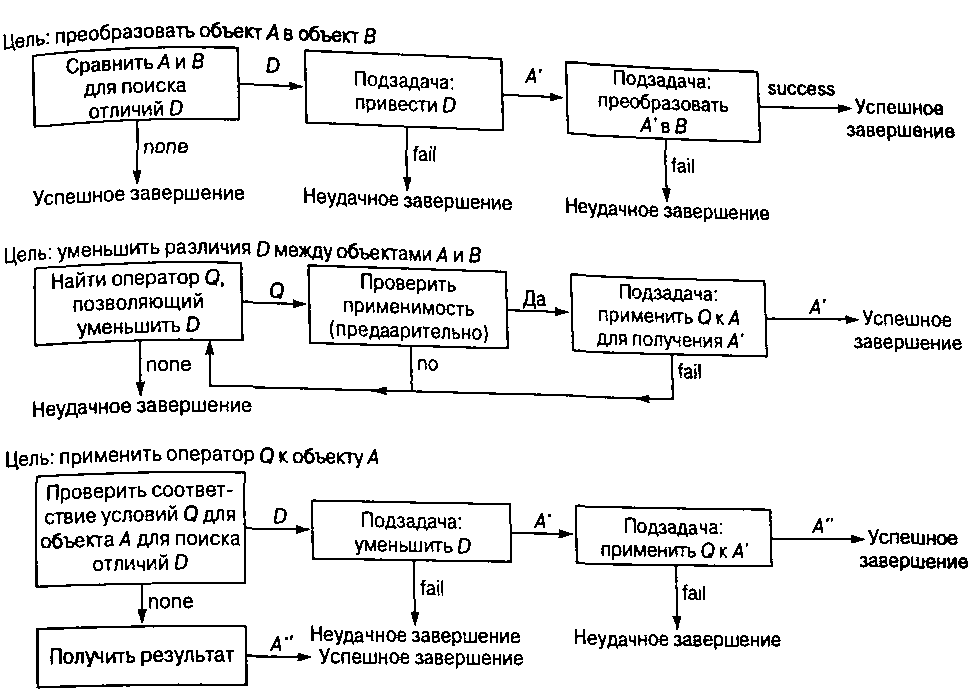
Для каждого типа цели система имеет стандартный метод:

1. Т(х, у) Ищется набор различий между начальным состоянием и целью. Если не имеется никакого различия, то решение найдено. Иначе, следует найти наиболее значимое различие, и ставиться цель уменьшить это различие. Если уменьшающаяся цель достигнута, то берется это состояние, и задается цель преобразовать это состояние до цели. Если уменьшающаяся цель терпит неудачу, берется следующее самое трудное различие, и делается попытка уменьшать это. Если не существует больше различий, тогда терпим неудачу.

2. С(О, D, х, у) Для уменьшающей цели ищется набор уместных операторов, выбирается самый трудный, и используется применяющаяся цель применить этот оператор к текущему состоянию. Если это не осуществляется, то цель достигнута. Если применяющая цель подводит, выбирается следующий самый трудный оператор. Если не больше операторов, тогда терпим неудачу.

3. А(О, х) Для применяющей цели проверяется, применим ли оператор. Находится набор всех вариантов оператора, которые являются применимыми, выбирается самый трудный и применяется. Если не имеется никаких применимых вариантов, находят набор различий между состоянием и областью оператора, выбирается самый трудный, и задается уменьшающаяся цель - уменьшить это различие на текущем состоянии. Если это уменьшает цель, следует, использовать применяющуюся цель - применить оператор к уменьшенному состоянию. Если уменьшающаяся цель терпит неудачу, пробуется следующее самое трудное различие для оператора. Если не больше различий, тогда терпим неудачу.

Стратегия может быть представлена в виде дерева, называемого деревом поиска.

41. Целенаправленные системы.

Система – список переменных в нашем представлении. Система характеризуется набором свойств, которые она пытается улучшить и этот набор свойств, мы можем определить как цель системы. Система анализирует ситуации принятия решения при взаимодействии целенаправленных систем.

В общем виде мы имеем n систем: I₁,…,I_n. Каждая из них имеет свою систему управления S_i.. Каждая система управления I_i имеет собственно управляющую подсистему, управляющие объекты, источники информации о внешней среде.

В каждый момент времени среда и элементы систем характеризуются определенными состояниями и набор этих состояний назовем ситуацией.

Ситуация может быть описана множеством отношений R между объектами внешней среды и элементами управления S_i.

На базе информации, поступающей от источников из внешней среды и элементов системы S_i , система S_i может построить информационную модель ситуации α, которую мы обозначим J_i(α) – информационная модель состояний α для системы S_i.

Само состояние модели J_i(α) может представлено или описано путем указания истинности некоторых предикатов P_ij(α). Эти предикаты соответствуют отношениям r_ij Є R_i, где R_i – множество отношений для системы S_i, которые определяются на основании данных источников информации системы S_i

Информационные модели J_i(α) естественно в общем случае различаются между собой, т.к. системы могут иметь различные модели одной и той же ситуации. На отношение r_ij так же воздействуют случайные воздействия для источников информации.

Обозначим через рефлексивные представления случаи, когда система S_i может иметь модель представлений о ситуации других систем S_j(j ≠ i) и будем записывать их как J_i (J_j(α)).

Такие модели могут использоваться для более точной оценки ситуации. Эти модели являются отражением системы S_i о степени осведомленности системы S_j.

Система S_i может определить свои возможности М_iⁱ по воздействию на внешнюю среду для достижения определенных состояний систем и обьектов.

На базе модели J_i(J_j(α)) система S_i может оценить возможности системы S_j, которое обозначим через M_i^j .

Система S_j может построить модель J_j(J_k(α)) – S_k модель М_к^j.

Т.е. система S_j может построить модель М_k^ij. На основании модели J_i(J_j1(J_jm(α))) мы можем построить модель возможностей системы S_i для систем М_jm^{jm-1,jm-2,…,j,i}. Цель для целеустремленной системы можно определить как некоторые желанные ситуации. Для системы S_i цель есть некоторая совокупность предложений, которые описывают желаемое свойство ситуации.

А_Jm^{Jm-1,Jm-2,…,J, I}– информационная модель совокупности предложений, которые описывают представление системы i о целевых установках системы S_Jm.

Рефлексивный процесс управления, как процесс принятия решения характеризуется определенным рангом рефлексии в зависимости от количества или состава используемых моделей.

Ранг = 0, если система, принимающая решение не имеет моделей целей других систем или пренебрегает ими. Однако, при этом система S_i может иметь модели других систем. Нулевой ранг рефлексии обычно используют ученые, которые считают, что природа неспособна к целенаправленному поведению, не стремится к достижению определенных целей.

На практике большое значение имеет целенаправленное воздействие на информационную модель ситуации для противоположной стороны путем применения дезинформации, демонстрация ложных целей. Это позволяет повлиять на представление противоположной стороны I₂ о своих возможностях М₂²¹. Спровоцировать противоположную сторону на изменение цели и дезинформировать сторону I₂ о своих возможностях и целевых установках.