Принципиальная последовательность этапов и работ по системному анализ

Последовательность этапов системного анализа	Методы анализа
Анализ проблемы  Существует ли проблема? Точное формулирование проблемы Анализ логической структуры проблемы Развитие проблемы (в прошлом и будущем) Внешние связи проблемы (с другими проблемами) Принципиальная разрешимость проблемы	2,4,7,9
Определение системы Формирование задач исходя из проблемы Определение позиции наблюдателя Определение объекта исследования Выделение элементов (определение границ расчленения системы) Определение подсистем Определение среды	1,5,10
Анализ структуры системы  Определение уровней иерархии Выделение подсистем Определение функциональных и структурных связей	2,5,6,8,10
Формулирование общей цели  и критерия системы Определение целей - требований надсистемы Определение ограничений среды Формулирование общей цели Определение критерия Декомпозиция критериев по подсистемам Композиция общего критерия из критериев подсистем	4,8,12
Декомпозиция цели, выявление потребности в ресурсах Формулирование целей верхнего ранга Формулирование целей подсистем Формулирование внешних ограничений Выявление потребностей в ресурсах	4,6
VI. Выявление ресурсов, композиция целей  Оценка существующей технологии и производственных мощностей Оценка современного состояния ресурсов Оценка возможностей взаимодействия с другими системами Оценка социальных факторов Композиция целей	1,3,6
VII. Прогноз и анализ будущих условий Анализ устойчивых тенденций развития системы Прогноз развития и изменения среды Предсказание появления новых факторов, оказывающих сильное влияние на развитие системы Анализ ресурсов будущего	1,3,5,6,8,9,10
Оценка целей и средств Вычисление оценок по критерию Оценка взаимозависимости целей Оценка относительной важности целей Оценка дефицитности и стоимости ресурсов Оценка влияния внешних факторов Вычисление комплексных расчетных оценок	1,3,7,8
Отбор вариантов  Анализ целей на совместимость Проверка целей на полноту Отсечение избыточных целей Разработка вариантов достижения отдельных целей Оценка и сравнение вариантов Совмещение комплекса взаимосвязанных вариантов	4,5,7,8
Производство Моделирование технологического и экономического процессов Расчет потенциальной и фактической мощности Проектирование организационной структуры Проектирование информационных механизмов Выявление недостатков организации производства и управления Выявление и анализ мероприятий по совершенствованию организации	2,3,5,6,7,10,11,12

№ п/п	Методы анализа	Этапы, на которых они применяются
1. 2. 3.	Неформальные методы Методы экспертных оценок Диагностические методы Метод аналогий	I,II,VI,IX I,III,IX,VIII,X VI,VIII,IX,X
4. 5. 6.	Графические методы Метод деревьев целей Матричные методы Сетевые методы	I,IV,V,VII,IX II,III,IX,VII,VIII,X III,V,VIII,IX
7. 8. 9.	Количественные методы Методы экономического анализа Морфологические методы Статистические методы	I,VI,VII,VIII,X III,IV,VI,VII I,VII
10. 11. 12.	Методы моделирования Кибернетические модели Описательные модели Нормативные операционные модели оптимизационные, имитационные, игровые и др.)	II,III,IV,VIII,X VIII,IX IV,VIII

29. Структурно-функциональный анализ систем..

Функциональный подход заставляет не только изучать конкретные потребности заказчика, исходя из реальных условий, но и глубже анализировать количественную и качественную стороны этих потребностей, последствия перестройки производства, организации сбыта продукции и т.д. Результат такого анализа - повышение обоснованности требований к тем или иным свойствам или характеристикам системы.

Функциональный анализ, проводимый при системных исследованиях, предполагает: рассмотрение любого объекта (системы) не в конкретной предметной форме, а как комплекса выполняемых функций; изучение каждой функции объекта как самостоятельной системы, реализуемой совокупностью материальных элементов и их связей, и в то же время - как части системы более высокого порядка. Например, технологический процесс, связанный с качественным изменением состояния объекта изготовления, входит в систему более высокого уровня - производственную. Поэтому при проведении функционального анализа технологического процесса обязателен анализ не только процесса, но и той части производственной системы, в рамках которой реализуется данная технология. Одновременно технологию следует рассматривать как систему, состоящую из подсистем - операций.Функция любого элемента структуры объекта, процесса может быть реализована на основе различных физико-химических и конструктивных принципов и средств их осуществления. Структурный анализ систем позволяет оценить соответствие структуры системы поставленным целям ее функционирования и достичь значительной экономии времени и средств при ее проектировании.Целями структурного анализа являются:

- разработка правил символического отображения систем;- оценка качества структуры системы;

- изучение структурных свойств системы в целом и ее подсистем;- выработка заключения об оптимальности структуры системы и рекомендаций по дальнейшему ее совершенствованию.

В зависимости от целей проведения структурного анализа системы ее структуру можно отобразить различными способами. Так, например, в теории автоматического регулирования наибольшее распространение получили структурные схемы, в электротехнике - электрические цепи и схемы их замещения, в теплоэнергетике - тепловые схемы и т.д.

30. Использование уравнения Ферхюльста.

В 1838 г. Ферхюльст предложил логическую модель, которая более достоверно описывает динамику популяций, чем модель Мальтуса. Более того, с помощью этой модели предсказывают множество сложных процессов в развитии человеческого общества и физических процессах.

Диапазон явлений, которые моделируют с помощью уравнений Ферхюльста, необыкновенно широк и постоянно увеличивается.

K- предельная емкость среды, т.е. можно ассоциировать с предельной численностью популяции.

Когда популяция мала N << K, то это уравнение совпадает с моделью Мальтуса. Для этого уравнения существует для точки равновесия: N = 0 – неустойчивая, N=K – устойчивая.

Это уравнение распространяется на N-мерный случай, когда мы имеем множество взаимодействующих систем.

С помощью такой системы моделировалась динамика мирового рынка основных энергетических ресурсов.

i – номер рассматриваемого энергоресурса;

-его объем;

соответствующие показатели (константы).

Были рассмотрены показатели по углю, нефти, газу, дереву в период с 1900 по 1920г.

Была выполнена на основе этих данных оценка показателей и прогнозировалась динамика до 1980. Точность 2-8%.

Статические данные о числе перевозимых авиапассажиров по отношению к километражу полета находятся в прекрасном соотношении с решением соответствующего логического уравнения.

31. Закон разнообразия Эшби.

При создании проблеморазрешающей системы необходимо, чтобы эта система имела большее разнообразие, чем разнообразие решаемой проблемы, или была способна создать такое разнообразие. Иначе говоря, система должна обладать возможностью изменять своё состояние в ответ на возможное возмущение; разнообразие возмущений требует соответствующего ему разнообразия возможных состояний. В противном случае такая система не сможет отвечать задачам управления, выдвигаемым внешней средой, и будет малоэффективной. Отсутствие или недостаточность разнообразия могут свидетельствовать о нарушении целостности подсистем, составляющих данную систему.

32. Теория Бреммермана.

В ней рассматривается физическое ограничение на объем вычислений. Любая активная деятельность, связанная с обработкой, хранением и воспроизведением информации должна основываться на материальном носителе.

Вопрос: сколько битов информации n может храниться в теле m?

Это число из современных физических соображений:

E_max— max. количество энергии, которую мы можем извлечь из тела массой m.

E=mc²; E—разрешение, с которым мы можем наблюдать один энергетический уровень и 1 бит кодируется одним энергетическим уровнем

Eth—соотношение неопределенностей Гейзенберга и h-постоянная Планка, t—продолжительность наблюдения.

Разделив формулы друг на друга получаем формулу:

Значит, что компьютер массой в 1г за секунду не сможет обработать > чем 210⁴⁷бит.

Пример парадоксального расчета

Возраст Вселенной оценивается на 10¹⁷сек, ее масса оценивается 10⁵⁸г. Получаем результат: Вселенная смогла бы обработать за время свой жизни 10¹²²бит.

Возьмем аэропорт: за сутки 1000запросов типа (дя/нет). Таким аэропортом управляет 20 диспетчеров.

Вопрос: какое количество информации проходит через них?

Полное число всевозможных ответов на такие запросы определяется известной формулой количества булевых функций от 1000 переменных:

Определим количество информации:

Это число больше 10¹²²

33. Рефлексивные системы.

Рефлексивный процесс управления, как процесс принятия решения характеризуется определенным рангом рефлексии в зависимости от количества или состава используемых моделей.

Ранг = 0, если система, принимающая решение не имеет моделей целей других систем или пренебрегает ими. Однако, при этом система S_i может иметь модели других систем. Нулевой ранг рефлексии обычно используют ученые, которые считают, что природа неспособна к целенаправленному поведению, не стремится к достижению определенных целей.

Рассмотрим две взаимодействующие системы I₁, I₂ с соответствующими системами управления S_1, S₂ . Обозначим через G_jⁱ –представление или модель задачи системы S_j стороны I_j c позиции стороны I_i , которая реализована в системе S_i .

a)рефлексия 0-ранга

Для ранга рефлексии 0 для системы S₁ ее задача имеет вид:

G₁¹ = {A₁¹, M₁¹, M₂¹ }.

Если система S₁ использует для принятия решения модель вида

G₁¹ = {A₁¹, M₁¹, A₂¹, M₂¹, M₁²¹}, где G₂¹ = { A₂¹, M₂¹, M₁²¹} есть представление системы S₂ о задаче S₁, то ранг рефлексии системы S₁ равен 1.

б) рефлексия 1-уровня

в)рефлексия 2-ранга

Для ранга рефлексии 2 для системы S₁ ее модель (задача) имеет вид:

G₁¹ = {A₁¹, M₁¹, M₂¹, A₂¹, A₁²¹, M₁²¹, M₂¹²¹}

Представление S₂ имеет 1 ранг рефлексии:

G₂¹ = {A₂¹, M₂¹, A₁²¹, M₂²¹, M₂¹²¹}

На практике большое значение имеет целенаправленное воздействие на информационную модель ситуации для противоположной стороны путем применения дезинформации, демонстрация ложных целей. Это позволяет повлиять на представление противоположной стороны I₂ о своих возможностях М₂²¹. Спровоцировать противоположную сторону на изменение цели и дезинформировать сторону I₂ о своих возможностях и целевых установках.

34. Естественный язык как системная модель мира.

Одним из основных способов изучения мышления человека является исследование языка.

Если ЕЯ человечества достаточно точно отражает внешний мир, то если мы сможем построить универсальную грамматика, то тем самым мы бы решили проблему понимания и познания внешнего мира.

Исследования ЕЯ сосредоточены на исследовании таких языков, которые имеют неординарные формы представления.

Основные направления:

1. Пространства, которое в большинстве естественных языков описывается через «наивную» физику человеческого тела, части которого являются основными координатами: право-лево, верх-низ.

2. Времени, т.е. языков, в которых обращено особое внимание на время (различающих 3 времени: настоящее, прошедшее, будущее), дающие циклические обозначения повторяющихся событий, описывающих действия или состояния события.

3. Языки, обращающие особое внимание на психическую жизнь, дающие представления о «я», как о говорящем и думающем и его границах.

4. Языки, в которых сильны мифологические основы и первобытные признаки науки.

Существуют нейрофизиологические данные о врожденности, размещениях функций, наименования или названия предметов, значений слов и грамматических конструкций, в определенных зонах полушарий мозга. Изучение естественного языка важно для проблемы перевода с внешнего естественного языка на внутренний машинно-компьютерный язык.

35. Влияние дискретности на неустойчивость поведения систем

Использование уравнения Ферхюльста

В 1838 г. Ферхюльст предложил логическую модель, с помощью которой предсказывают множество сложных процессов в развитии человеческого общества и физических процессах.

Это основное уравнение для описания самоорганизующихся систем.

K- предельная емкость среды, т.е. можно ассоциировать с предельной численностью популяции.

Для этого уравнения существует для точки равновесия: N = 0 – неустойчивая, N=K – устойчивая.

Это уравнение распространяется на N-мерный случай, когда мы имеем множество взаимодействующих систем.

С помощью такой системы моделировалась динамика мирового рынка основных энергетических ресурсов.

i – номер рассматриваемого энергоресурса; -его объем; соответствующие показатели (константы).

Влияние дискретности на развитие неустойчивостей

аналогии между математическими моделями взаимодействия в различных сферах деятельности. При математическом моделировании физических процессов предпочтение отдается дифференциальной форме записи, когда пространство и время меняются непрерывно.

В социальной сфере дискретность изменения событий отражается в разностных уравнениях, где результат предыдущего действия, является начальным значением последующего действия.

Но в определенных случаях переход от непрерывной формы записи к дискретной пожжет повлиять на асимптотическое поведение системы.

Сравнение на ур-ии Ферхюльста

y^' = r (1-y) y это линейное диф. ур-ние 1-го рода (Ферхюльста), явл. характерным для нелинейной динамической системы, имеющей ограничения на мах зн-ие.

Таким уравнением описывают: изменение численности насекомых в условиях ограниченности питательной среды; рост концентрации электронов в полупроводнике под действием лазерного излучения при насыщении числе разрешенных состояний; св-ва турбулентных потоков.

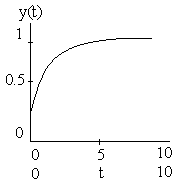
Независимо от значения параметра r функция y асимптотически стремится к 1 – нормированному мах значению.

Асимптотическое поведение динамической системы с ограниченным ресурсом при непрерывном изменении события.

Уравнение, записанное в разностной форме y_n+1 = y_n (1+r) – r*y_n² дает аналитическое решение, пока параметр r не начинает превышать 1. Но если r>2 изначально детерминированный процесс становится хаотичным.

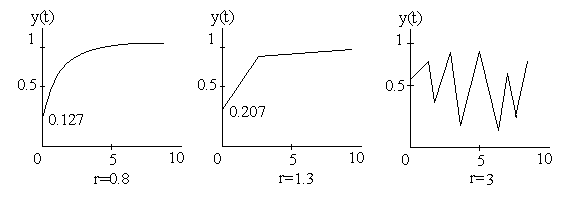
Определяющим в данном превращении является вклад членов с положительной обратной связью. Для наглядной демонстрации введем в слагаемые выражения (2) разные коэффициенты r1, отвечающий за положительную обратную связь и r2, отвечающий за отрицательную обратную связь y_n+1 = y_n (1+r1) – r2*y_n² и будем изменять их значения.

Получаем, что если r1 > 2 , то увеличение r2 может только замедлить развитие флуктуации и снизит уровень, относительно которого система флуктуирует, но не стабилизировать процесс.

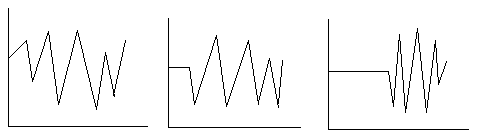
Влияние роста r2 на ход процесса при различных r1.

36. Проблема определения новых терминов.

Проблема определения в языке - определение новых терминов.

Рассмотрим известный парадокс Греллинга. Некоторые прилагательные, к примеру "многосложное", "русское" обладают тем же самым свойством, которое они означают, т.е. "русское"-есть русское, "многосложное"-есть многосложное. Большинство прилагательных этим свойством не обладают - горячее, холодное, красное, арабское, немецкое.

Назовем прилагательные второго рода гетерологическими.

Обнаруживаем, что прилагательное "гетерологическое" является гетерологическим в том случае, если оно является негетерологическим.

Парадокс Ришара.

Рассмотрим все такие действительные числа, которые могут быть охарактеризованы при помощи конечной последовательности русских слов. К примеру: «8/9», «положительный квадратный корень из девяти», «наименьшее число, удовлетворяющее условию, что сумма квадрата этого числа и его произведение на 2 равна 3». Существует счетное число таких чисел. Обозначим это множество через R и произведем нумерацию его элементов произвольным образом. Охарактеризуем некоторое число r, как «такое действительное число из интервала [0,1], что его n-ый десятичный знак есть результат циклического сдвига n-го десятичного знака n-го числа в нашей нумерации». Получаем, что r отличается от любого элемента R. Потому оно не может быть однозначно охарактеризовано конечной последовательностью русских слов. Получаем противоречие, т.к. r мы уже охарактеризовали конечной последовательностью русских слов.

Закончим проблему определения притчей.

Вопрос: знаете ли вы в чем истина всех вещей?

Ответ: как я могу знать это?

Вопрос: знаете ли вы того, чего не знаете?

Ответ: как я могу это знать?

Вопрос: стало быть, никто ничего не знает?

Ответ: как я могу это знать, но все же попробую рассказать: «как знать, что то, что называется знанием, не является незнанием и как знать, что то, что я называю незнанием, не называется знанием?»