26 Численные методы восстановления функций: постановка задачи.

В вычислительной практике часто приходится иметь дело с функциями , заданными таблицами их значений для некоторого конечного множества значений х: .

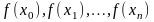В процессе же решения задачи необходимо использовать значения для промежуточных значений аргумента. В этом случае строят функцию Ф(x), достаточно простую для вычислений, которая в заданных точках x₀, x₁,...,x_n, называемых узлами интерполяции, принимает значения , а в остальных точках отрезка (x₀,x_n), принадлежащего области определения , приближенно представляет функцию с той или иной степенью точности.

При решении задачи в этом случае вместо функции оперируют с функцией Ф(x). Задача построения такой функции Ф(x) называется задачей интерполирования. Чаще всего интерполирующую функцию Ф(x) отыскивают в виде алгебраического полинома.

27 Численные методы восстановления функций: интерполяция полиномом Лагранжа. Интерполяционные формулы Лагранжа и Ньютона.

Для каждой функции , определенной на [a,b], и любого набора узлов x₀, x₁,....,x_n( x_i 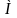[a,b], x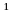_i x_j при i j ) среди алгебраических многочленов степени не выше n существует единственный интерполяционный многочлен Ф(x), который может быть записан в форме:

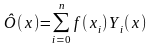, (4.1)

где - многочлен n-ой степени, обладающий следующим свойством:

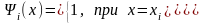
(4.2)

Для интерполяционного полинома многочлен имеет вид:

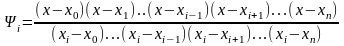(4.3)

Этот многочлен (4.1) и решает задачу интерполирования и называется интерполяционным полиномом Лагранжа.

1. Пример

В качестве примера рассмотрим функцию вида 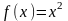на интервале 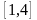заданную табличным способом.

X	1	2	3	4
F(x)	1	4	9	16

Необходимо определить значение функции в точке x-2.5. Воспользуемся для этого полином Лагранжа. Исходя из формул (4.1 и 4.3) запишем этот полином в явном виде:

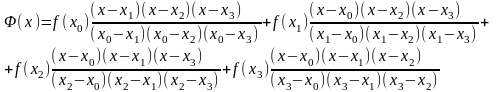(4.4).

Тогда подставляя в формулу (4) исходные значения из нашей таблицы получим

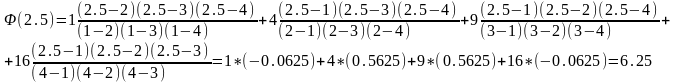
Полученный результат соответствует теории т.е. .

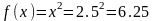2. Интерполяционная формула Лагранжа

Интерполяционный полином Лагранжа может быть записан в другой форме:

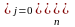(4.5)

Запись полинома в виде (4.5) более удобна для программирования.

Интерполяционным полиномом Ньютона называется полином (3.2.8):

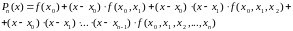(3.2.8)

где

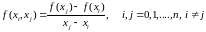- раздельная разность первого порядка,

- раздельная разность второго порядка,

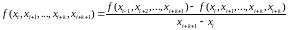- раздельная разность 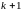порядка.

Раздельная разность 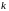- го порядка вычисляется так (3.2.9),

(3.2.9)

28 Численные методы восстановления функций: погрешность интерполирования (остаточный член интерполяционной формулы и оптимальный выбор узлов).

При решении задачи интерполяции величина n называется порядком интерполирующего полинома. При этом, как видно из формул (4.1) и (4.5), число узлов интерполирования всегда будет равно n+1 и значение x, для которого определяется величина , должно лежать внутри области определения узлов интерполяции т.е.

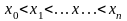. (4.6)

В некоторых практических случаях общее известное число узлов интерполяции m может быть больше, чем порядок интерполирующего полинома n.

В этом случае, прежде чем реализовывать процедуру интерполяции согласно формуле (4.5), необходимо определить те узлы интерполяции, для которых справедливо условие (4.6). При этом следует помнить, что наименьшая погрешность достигается при нахождении значения x в центре области интерполяции. Для обеспечения этого предлагается следующая процедура:

1. После ввода в программу значения величины х необходимо проверить условие x₀  x  x_m, где x₀ и x_m – начальное и конечное значение узловых точек интерполяции.

2. При выполнения предыдущего условия начинается поиск области интерполяции, для чего находим первое x_i такое, для которого выполняется условие x_i > x, при этом номер i будет соответствовать середине интервала интерполяции. Для определения области интерполяции ее левая граница будет начинаться с номера 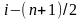, а заканчиваться узлом с номером .

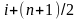3. После выполнения пунктов 1 и 2 программируется формула (4.5).

Основное назначение интерполяции – это вычисление значений табулированной функции для неузловых (промежуточных) значений аргумента, поэтому интерполяцию часто называют «искусством чтения таблиц между строками».

Остаточный член интерполяционной формулы

Заменяя функцию 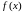интерполяционным полиномом 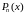, мы допускаем погрешность (3.3.1):

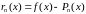(3.3.1)

которая называется погрешностью интерполирования или остаточным членом интерполяционной формулы.

В узлах интерполирования эта погрешность равна нулю.

Погрешность интерполирования определяется следующим соотношением (3.3.2):

(3.3.2)

где и

Отсюда следует оценка точности восстановления функции (3.3.3):

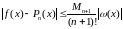(3.3.3)

где

(3.3.4)

где .

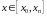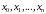В частности, если - алгебраический многочлен степени , то интерполирование, проведено по любым точкам , осуществляется точно.

Данная оценка справедлива как для формулы Лагранжа. Та ки для формулы Ньютона.