30 Численные методы восстановления функций: метод наименьших квадратов.

Если набор экспериментальных данных (узлов интерполяции) получен со значительной погрешностью, то не имеет смысла использовать интерполяцию Лагранжа полиномами или сплайнами. В этом случае необходимо провести аппроксимирующую кривую, которая не проходит через экспериментальные точки (узлы), но в то же время отражает исследуемую зависимость.

Пусть восстанавливаемая функция задана таблицей 1 на интервале .

Таблица 1

x	f(x)
x0	f0
…	…
xn	fn

Введем непрерывную функцию 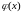для аппроксимации функции .

Отклонение функции от в узловых точках определяется (3.5.1):

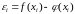(3.5.1)

Потребуем, чтобы сумма квадратов отклонений аппроксимирующей функции от восстанавливаемой в узловых точках была минимальна (3.5.2):

(3.5.2)

Такой способ построения аппроксимирующей функции называется метод наименьших квадратов (МНК).

Наиболее распространен способ выбора функции в виде линейной комбинации (3.5.3):

(3.5.3)

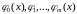- базисные функции; 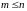; - коэффициенты, которые определяются из условия (3.5.2).

Условия минимума функции 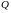: частные производные по коэффициентам должны быть равны нулю(3.5.4):

(3.5.4)

Из системы (3.5.4) определяются коэффициенты .

В матричном виде система (3.5.4) выглядит так (3.5.5):

Матрица системы (3.5.4) имеет вид (3.5.5):

, (3.5.5)

где

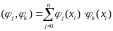- скалярное произведение базисных функций.

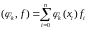- скалярные произведения элементов столбца свободных членов.

Пример.

Восстанавливаемая функция задана таблицей:

x	f(x)
x0	f0
…	…
xn	fn

В качестве аппроксимирующей функции возьмем .

Требуется определить коэффициенты .

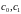1)

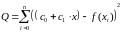
2) Найдем производные по и приравняем их к нулю:

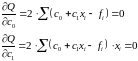
3) Тогда решив данные уравнения, получим коэффициенты :

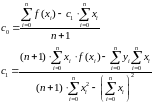
31 Методы численного интегрирования: постановка задачи, метод прямоугольников.

Простейшим полиномом является константа. В формуле прямоугольников функция аппроксимируется своим значением в точке a (или в точке b), т.е.

(5.1)

Если значение функции берется в точке a, то формула (5.1) носит название формулы левых прямоугольников.

Р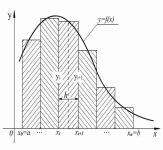 ис 5.2. Метод средних прямоугольников.

Для подсчета интеграла разделим интервал интегрирования 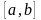на n равных отрезков длины . На каждом из отрезков функция заменяется прямоугольником с отрезками как основаниями, равными h и вертикальными боковыми сторонами высотой f(x_i). При этом точка x_i выбирается, как середина каждого элементарного отрезка. Метод “средних” прямоугольников (метод средних) является более точным, чем методы “левых” и “правых” прямоугольников, когда в качестве точек 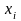могут выбираться левые или правые границы элементарных отрезков.

С геометрической точки зрения означает, что площадь криволинейной трапеции , ограниченной графиком функции , осью абсцисс и двумя прямыми x=a и x=b, принимается приближенно равной площади ступенчатой фигуры, образованной из n прямоугольников с основаниями и высотами f(x_i) где ..

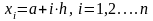Для интервала и шага интегрирования h полная формула будет записана в виде:

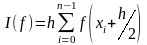(5.2)

где n - число разбиений для интервала [a,b], и точка x₀ совпадает с a.