15.Применение электромагнитной индукции

4.6. Примеры применения закона электромагнитной индукции.

Рассмотрим ряд примеров на применение основного закона электромагнитной индукции Фарадея.

1) Движение проводника в однородном магнитном поле (рис.14.3).

Рис.14.3.

2) Вращение проводника в однородном магнитном поле (рис.14.4).

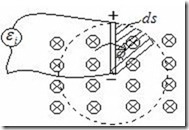
Рис.14.4.

1 2

3) Трансформатор (рис.14.5).

  , где

,  ,

Рис.14.5.

то есть поток индукции магнитного поля, созданного током в первичной обмотке, через витки вторичной обмотки есть:

.Полагая, что сила тока в первичной обмотке изменяется по закону  , находим искомую ЭДС, наводимую во вторичной обмотке:

.

Амплитудное (максимальное) значение ЭДС равно:

.

18.Сложение гармонических колебаний одного направления и одной частоты.

Колеблющееся тело может принимать участие в нескольких колебательных процессах, тогда следует найти результирующее колебание, другими словами, колебания необходимо сложить. В данном разделе будем складывать гармонические колебания одного направления и одинаковой частоты    применяя метод вращающегося вектора амплитуды, построим графически векторные диаграммы этих колебаний (рис. 1). Tax как векторы A₁ и A₂ вращаются с одинаковой угловой скоростью ω₀, то разность фаз (φ₂ - φ₁) между ними будет оставаться постоянной. Значит, уравнение результирующего колебания будет   (1)  В формуле (1) амплитуда А и начальная фаза φ соответственно определяются выражениями   (2)    Значит, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает при этом также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (φ₂ - φ₁) складываемых колебаний. 

Рис.1

Исследуем выражение (2) в зависимости от разности фаз (φ₂ - φ₁):  1) φ₂ - φ₁ = ±2mπ (m = 0, 1, 2, ...), тогда A=A₁+A₂, т. е. амплитуда результирующего колебания А будет равна сумме амплитуд складываемых колебаний;  2) φ₂ - φ₁ = ±(2m+1)π (m = 0, 1, 2, ...), тогда A=|A₁–A₂|, т. е. амплитуда результирующего колебания будет равна разности амплитуд складываемых колебаний.  Для практики представляет особый интерес случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте. После сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой. Периодические изменения амплитуды колебания, которые возникают при сложении двух гармонических колебаний с близкими частотами, называются биениями.  Пусть амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω<<ω. Выберем начало отсчета так, чтобы начальные фазы обоих колебаний были равны нулю:    Складывая эти выражения и учитывая, что во втором сомножителе Δω/2<<ω, получим   (3)  Результирующее колебание (3) можно считать как гармоническое с частотой ω , амплитуда А_σ которого изменяется по следующему периодическому закону:   (4)  Частота изменения А_σ в два раза больше частоты изменения косинуса (так как берется по модулю), т. е. частота биений равна разности частот складываемых колебаний:    Период биений    Вид зависимости (3) показан на рис. 2, где сплошные жирные линии представляют график результирующего колебания (3), а огибающие их линии - график медленно меняющейся согласно уравнению (4) амплитуды. 

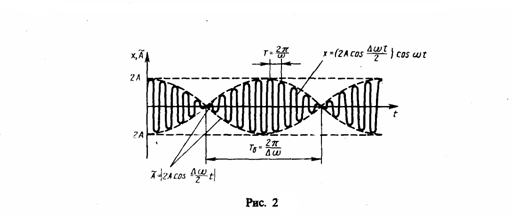
Рис.2

Нахождение частоты тона (звука определенной высоты) биений между эталонным и измеряемым колебаниями — наиболее часто используемый на практике метод сравнения измеряемой величины с эталонной. Метод биений применяется для настройки музыкальных инструментов, анализа слуха и т. д.  При исследовании сложного колебательного процесса нужно знать, что любые сложные периодические колебания s=f(t) можно представить в виде суперпозиции (наложения) одновременно совершающихся гармонических колебаний с различными амплитудами, начальными фазами, а также частотами, которые кратны циклической частоте ω₀ :   (5)  Представление в виде (5) любой периодической функции связывают с понятием гармонического анализа сложного периодического колебания, или разложения Фурье. Слагаемые ряда Фурье, которые определяют гармонические колебания с частотами ω₀, 2ω₀, 3ω₀, ..., называются первой (или основной), второй, третьей и т. д. гармониками сложного периодического колебания. Незатухающие механические колебания. Математический маятник.

Математи́ческий ма́ятник — осциллятор, представляющий собоймеханическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебанийматематического маятника длины l неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен

и не зависит^[1] от амплитуды и массы маятника.