Процесс изменения характера движения тела происходит при его силовом взаимодействии с другими телами. Для количественного описания процесса  вводят понятия силы и работы, совершаемой силой.

1.Если на тело действует постоянная сила F (Рисунок 13), и это приводит к перемещению ∆ r тела, тоэлементарной работой ∆А постоянной силы называется скалярное произведение вектора силы Fи вектора перемещения ∆r:

∆А = (F∙∆r) =  ½ F½½∆ r½ cos a , где a - угол между направлениями векторов силы F и перемещения ∆r, ( F∙ ∆r) – скалярное произведение двух векторов (см.[8]).

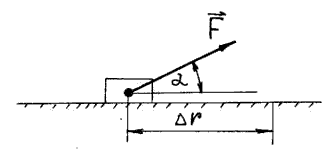
Рисунок 13 - Перемещение тела под действием постоянной силы.

Работа ∆А - скаляр. Если угол a - острый, то ∆А  положительная величина, и говорят, что сила совершает работу. Если угол a - тупой, то ∆А - отрицательная  величина, и говорят, что работа совершается против действия силы. Если  a = 90⁰, т.е. направления силы и перемещения взаимно перпендикулярны, то такая сила работы не совершает ∆А = 0. Такая сила не может изменить величину скорости тела, но она меняет направление скорости.

2. Работа переменной силы. Если сила или равнодействующая сил изменяет свою величину или направление (движение по криволинейной траектории, причем угол α  ≠ 90⁰), то работа  ∆А, совершаемая переменной силой F (или Fрез) на конечном участке траектории вычисляется следующим образом.

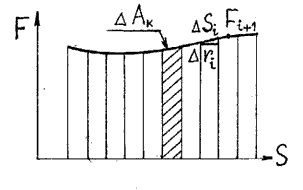
На рисунке 14 представлен график зависимости силы F от пути S. Разобьем весь путь на N участков. Перемещение и действующая сила на каждом участке соответственно равны F _i и ∆ r _i. Тогда работа А, совершаемая силой F,  равна алгебраической сумме работ, совершаемых  каждой из сил F _i на своем  малом   участке  (Рисунок 14):

А = ∆А₁ + ∆А₂ +....+ ∆А _N =  ( F₁∙∆ r₁) + (F ₂∙∆ r₂) + ...+( F _N∙∆ r_N) =    ( F_i∙∆ r_i),

где i = 1,2...... N - номер элементарного  участка траектории.

Рисунок 14 - График зависимости силы от пути.

На участке ∆r _i силу F_i  можно считать постоянной, тогда элементарная работа ∆А_i на участке ∆r_i равна ∆А_i= F_i∙∆ r _i и равна площади заштрихованной фигуры на  рисунке 14.

А= ∆А_i - это работа силы F на участке r, равна она численно площади S фигуры, ограниченной кривой зависимости F(х) и осью Х.

3.Примеры вычисления работы.

а) Тело, поднятое над землей на высоту h, падает на землю (без трения) из точки В в точку С и возвращается обратно (Рисунок 15). Определить работу силы по замкнутому пути.

Сила, действующая на тело, постоянна и равна силе притяжения тела к Земле (сила тяжести). Работа этой силы на участке ВС равна   .

Чтобы поднять тело без ускорения из точки С в точку В, надо приложить к телу силу, равную силе тяжести, но противоположно направленную, и работа на участке пути СВ равна   (работа совершается против силы тяжести).

Полная работа на участке (ВС+СВ) равна нулю.

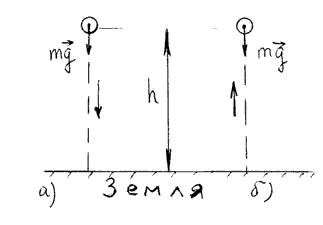
Рисунок 15. Падение тела с высоты h (a) и поднятие тела на высоту h (б)

б) Пружину длиной l₁ растягиваем  до длины l₂. Какая работа при этом  совершается?

Пусть х - длина, на которую  растянута пружина, отсчет х от положения равновесия (Рисунок 16). При этом на пружину будет действовать упругая сила, старающаяся вернуть пружину в состояние равновесия, что соответствует минусу в формуле F = - kх (закон Гука). Если растянуть пружину еще на малую длину ∆х, надо совершить элементарную работу ∆А = - kх∙ ∆х.

Возникающая упругая сила будет переменной, т.к. она зависит от длины, на которую растягивают пружину. Для определения работы, которую надо затратить для растяжения пружины от длины l₁ до l₂, надо воспользоваться операцией интегрирования:

Работа силы упругости определяется только начальным и конечным положением пружины.

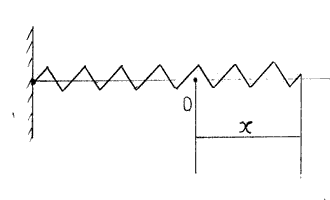
Рисунок 16. Сжатие пружины

4. Полная работа внешних сил при вращательном движении тела равна произведению момента этих сил относительно оси вращения  на угол поворота тела за время действия сил.   ∆ A= М∆ .

И момент сил, и угловое перемещение (равное по модулю углу поворота)  - векторы, направленные вдоль оси вращения.  Если направление этих векторов совпадает, то ∆ A>0. Если направление этих векторов противоположное, то ∆ A<0.

5. Силы, работа которых определяется только начальной и конечной точками их приложений,  и не зависят ни от вида траектории, ни от характера движения тела, называются консервативными илипотенциальными силами.Другое определение для этих сил таково. Силы, работа которых по замкнутой траектории равна нулю, называются потенциальными.Соответственно, если работа силы по замкнутой траектории не равна нулю, то такая силанеконсервативная ( непотенциальная).К непотенциальным силам относятся силы трения и силы, величина которых зависит от скорости движения точки (тела).Сила тяжести и сила упругости являются потенциальнымисилами (см. приведенные выше примеры)

4. Законы сохранения импульса телЗако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.Как и любой из фундаментальных законов сохранения, закон сохранения импульса описывает одну из фундаментальных симметрий, — однородность пространства.

Рассмотрим второй закон Ньютона

Перепишем его для системы из N частиц:

где суммирование идет по всем силам, действующим на n-ю частицу со стороны m-ой. Согласно третьему закону Ньютона, силы вида   и   будут равны по абсолютному значению и противоположны по направлению, то есть  Тогда после подстановки полученного результата в выражение (1) правая часть будет равна нулю, то есть:

или

Как известно, если производная от некоторого выражения равна нулю, то это выражение есть постоянная величина относительно переменной дифференцирования, а значит:

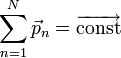 (постоянный вектор).

То есть суммарный импульс системы частиц есть величина постоянная. Нетрудно получить аналогичное выражение для одной частицы.

Следует учесть, что вышеприведенные рассуждения справедливы лишь для замкнутой системы.

Также стоит подчеркнуть, что изменение импульса   зависит не только от действующей на тело силы, но и от продолжительности её действия.

5. Законы сохранения энергии в механике.

В ньютоновской механике формулируется частный случай закона сохранения энергии — Закон сохранения механической энергии, звучащий следующим образом^[2]

Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной.

Проще говоря, при отсутствии диссипативных сил (например, сил трения) механическая энергия не возникает из ничего и не может исчезнуть никуда.

[править]Примеры

Классическим примером этого утверждения являются пружинный или математический маятники с пренебрежимо малым затуханием. В случае пружинного маятника в процессе колебаний потенциальная энергия деформированной пружины (имеющая максимум в крайних положениях груза) переходит в кинетическую энергию груза (достигающую максимума в момент прохождения грузом положения равновесия) и обратно^[3]. В случае математического маятника^[4] аналогично ведёт себя потенциальная энергия груза в поле силы тяжести.

[править]Вывод из уравнений Ньютона

Закон сохранения механической энергии может быть выведен из второго закона Ньютона^[5], если учесть, что в консервативной системе все силы, действующие на тело, потенциальны и, следовательно, могут быть представлены в виде

,

где   — потенциальная энергия материальной точки (  — радиус-вектор точки пространства). В этом случае второй закон Ньютона для одной частицы имеет вид

,

где   — масса частицы,   — вектор её скорости. Скалярно домножив обе части данного уравнения на скорость частицы и приняв во внимание, что  , можно получить

Путём элементарных операций это выражение может быть приведено к следующему виду

Отсюда непосредственно следует, что выражение, стоящее под знаком дифференцирования по времени, сохраняется. Это выражение и называется механической энергией материальной точки. Первый член в сумме отвечает кинетической энергии, второй — потенциальной.

Этот вывод может быть легко обобщён на систему материальных точек^[2].

6.Закон сохранения момента импульса.

 Для замкнутой системы тел момент внешних сил всегда равен нулю, так как внешние силы вообще не действуют на замкнутую систему.         Поэтому  , то есть

         или         

       Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени.         Это один из фундаментальных законов природы.         Аналогично для замкнутой системы тел, вращающихся вокруг оси z:

         отсюда                   или          .

       Если момент внешних сил относительно неподвижной оси вращения тождественно равен нулю, то момент импульса относительно этой оси не изменяется в процессе движения.         Момент импульса и для незамкнутых систем постоянен, если результирующий момент внешних сил, приложенных к системе, равен нулю.         Очень нагляден закон сохранения момента импульса в опытах с уравновешенным гироскопом – быстро вращающимся телом, имеющим три степени свободы (рис. 6.9).

       Используется гироскоп в различных навигационных устройствах кораблей, самолетов, ракет (гирокомпас, гирогоризонт). Один из примеров навигационного гироскопа изображен на рисунке 6.10.         Именно закон сохранения момента импульса используется танцорами на льду для изменения скорости вращения. Или еще известный пример – скамья Жуковского (рис. 6.11).