2. Внешний фотоэффект

Внешний фотоэлектрический эффект - испускание электронов из вещества под действием света (излучения). Если электроны вылетают за пределы вещества, то фотоэффект называют внешним. Он наблюдается главным образом у металлов. Вылетающие с поверхности металла электроны называют фотоэлектронами, а регистрируемый в цепи ток – фототоком.

Фотоэффект был открыт Герцем в 1887 г. Столетов изучал фотоэффект на установке, изображенной на Рис.2а, которая позднее была усовершенствована другими исследователями (Рис.2б)

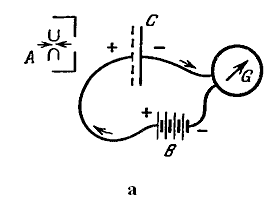
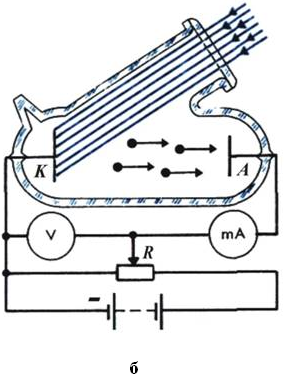
Рис.2а – схема установки Столетова, где А – источник излучения, B - источник Э.Д.С., С – конденсатор, состоящий из проволочной сетки и сплошной пластины, G – гальванометр; б – установка Ленарда и других исследователей для изучения фотоэффекта, где К и А – катод и анод фотоэлемента, V – вольтметр, mA - миллиамперметр, измеряющий фототок, R - реостат.

Герцем и Столетовым были установлены следующие законы фотоэффекта:

1. Максимальная сила фототока (тока насыщения) пропорциональна световому потоку, падающему на катод.

2. Максимальная скорость фотоэлектронов увеличивается с ростом частоты (с уменьшением длины волны) падающего света и не зависит от интенсивности светового потока.

3. Независимо от интенсивности светового потока фотоэффект начинается только при определенной для данного металла минимальной частоте (максимальной длине волны) света, называемой красной границей фотоэффекта.

Классическая теория не смогла объяснить законы фотоэффекта. Чтобы сделать это А. Эйнштейн предположил, что свободный электрон проводимости в металле поглощает квант света . Часть энергии поглощенного (и переставшего существовать) кванта, полученная электроном, затрачивается на работу выхода из металла, которую он совершает против сил притяжения со стороны положительного заряда ионов кристаллической решетки. Кроме того, между электронами проводимости в металле и электронами, вылетевшими из металла в результате термоэлектронной эмиссии устанавливается динамическое равновесие и возникает тонкий запирающий слой, напряженность электрического поля которого направлена наружу (по отношению к поверхности металла). Электрон, вылетающий из металла в результате фотоэффекта должен преодолеть этот запирающий слой.

Закон сохранения энергии для фотоэффекта (формула Эйнштейна) имеет вид:

,

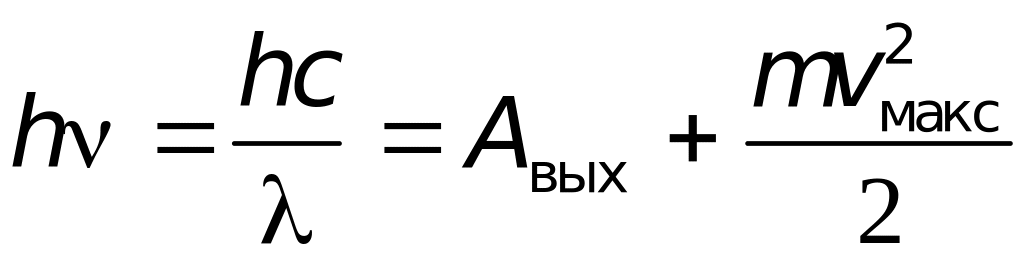где – работа выхода электрона из вещества, –максимальная кинетическая энергия электрона, – энергия поглощенного кванта, –постоянная Планка, – масса электрона.

Если электрон поглощает квант света не у самой поверхности, а на некоторой глубине, то часть его кинетической энергии может быть потеряна в результате случайных столкновений в металле. Кинетическая энергия электрона будет максимальной, если электрон избежит указанных столкновений.

Из уравнения Эйнштейна следует, что 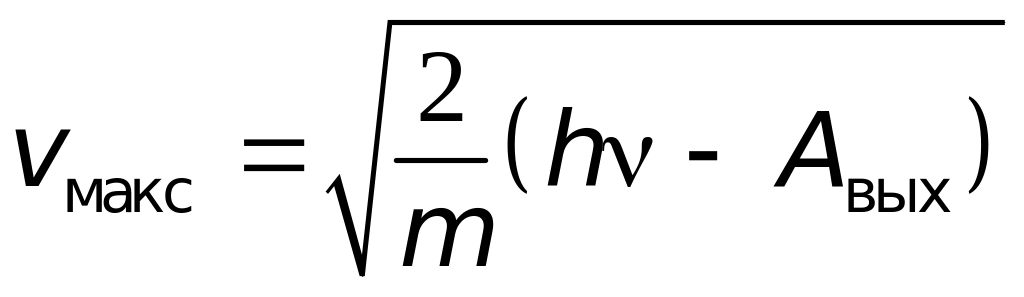, зависит от частоты излучения, но не зависит от его интенсивности.

В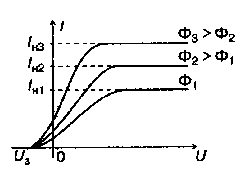 ольтамперная характеристика (зависимость фототока от анодного на пряжения )

Рис. 3. Вольтамперные характеристики фотоэлемента для одной частоты падающего излучения и разных световых потоков .

Характер кривых вольтамперных характеристик фотоэлемента (Рис.3) объяс-няется следующим образом. Электроны вылетают из катода с различными по величине скоростями. При U = 0 лишь часть испущенных электронов, обладающих достаточно большими скоростями, достигает анода. При некотором положительном напряжении (U > 0) фототок достигает насыщения - все электроны, испущенные катодом, попадают на анод. Чем больше световой поток Ф, тем больше квантов света поглощается электронами в единицу времени, тем больше электронов вылетает из металла и, следовательно, тем больше ток насыщения I_н = k·Ф. Для прекращения фототока необходимо приложить достаточное по величине отрицательное напряжение U_з, называемое задерживающим. В этом случае выполняется условие (e — заряд электрона, m — его масса, — задерживающее напряжение) и ни одному из электронов не удастся преодолеть задерживающее электрическое поле и достичь анода. Вольтамперная характеристика позволяет определить число электронов, вылетающих из катода в единицу времени и максимальную кинетическую энергию электронов, которая выражается через задерживающее напряжение. Коэффициент пропорциональности k (мкА/Вт), соответствующий силе фототока (выраженной в микроамперах) при освещенности катода световым потоком 1 Вт, называют фоточувствительностью элемента. Фототок насыщения I_н = е·n, где n — число электронов, испускаемых катодом в 1 с. Зависимость фототока насыщения от светового потока носит название световой характеристики фотоэлемента (Рис. 4).

Рис.4 Световая характеристика фотоэлемента

Поскольку , то уравнение Эйнштейна можно записать в виде:

.

В случае если энергия фотона много больше работы выхода ( ), то

Внешний фотоэффект считается состоявшимся, если электрон выходит из металла с нулевой скоростью. Максимальная длина волны падающего кванта или минимальная частота ₀, ₀, при которой это происходит, называется красной границей фотоэффекта.

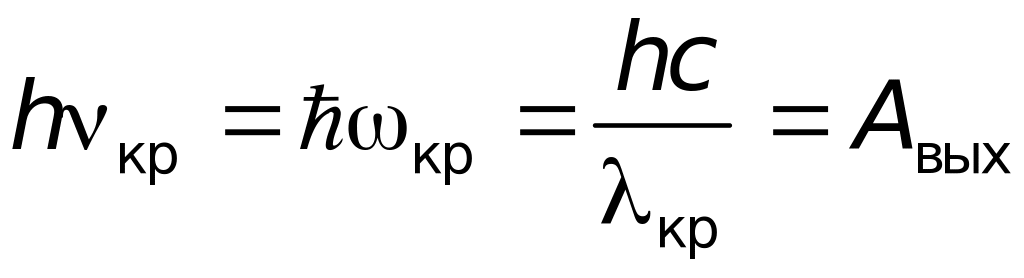
Красной граница фотоэффекта называется потому, что увеличение длины волны падающего света до максимально возможной соответствует смещению в сторону красной границы для видимого спектра. При меньшей частоте падающего света (большей длине волны) фотоэффект не наблюдается.

Энергию фотонов и работу выхода принято выражать во внесистемных единицах - электронвольтах (эВ). Один электронвольт равен энергии, приобретенной электроном при прохождении разности потенциалов 1В: 1 эВ = 1,610^-19 Дж.

Экспериментально было обнаружено, что зависимость от  для данного металла имеет вид наклонной прямой, причем наклон прямых, построенных для разных металлов, оказался одинаковым.

Из соотношения вытекает уравнение, соответствующее экспериментальной зависимости, показанной на Рис.5,

.

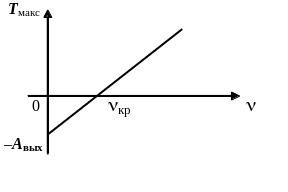
Рис. 5 Зависимость максимальной кинетической энергии фотоэлектронов от частоты падающего света

Если электрон в металле является свободным (не связанным с атомом), то фотоэффект не состоится. Законы сохранения импульса и энергии для фотоэффекта в этом случае имели бы вид (до взаимодействия с фотоном электрон покоился):

,

где p – импульс электрона, - энергия покоя электрона; - энергия электрона, который после поглощения фотона приобрел импульс .

Возведя полученные соотношения в квадрат, получим

.

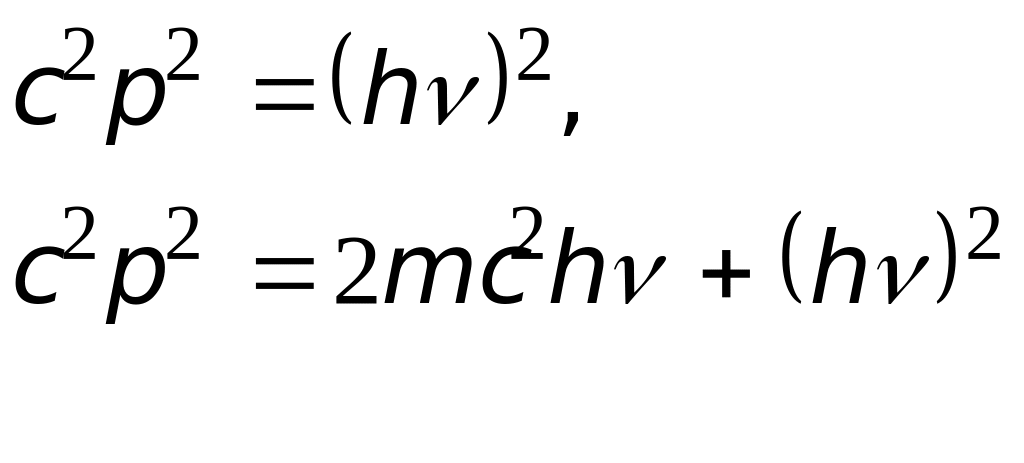При эти равенства несовместимы, откуда следует, что свободный электрон не может поглотить фотон.

Задача 1. Определите максимальную скорость фотоэлектронов, вырываемых с поверхности серебра:

1. ультрафиолетовым излучением с длиной волны 155 нм;

2.  - излучением с длиной волны 2,47 пм.

Работа выхода электрона из серебра равна 4,7 эВ.

Решение. Кинетическая энергия фотоэлектрона зависит от энергии фотона

, вызывающего фотоэффект. Если энергия фотона много меньше энергии покоя

электрона , то кинетическая энергия фотоэлектрона выражается по классической формуле , а если сравнима по величине или больше , то по релятивистской .

1. Энергия фотона равна:

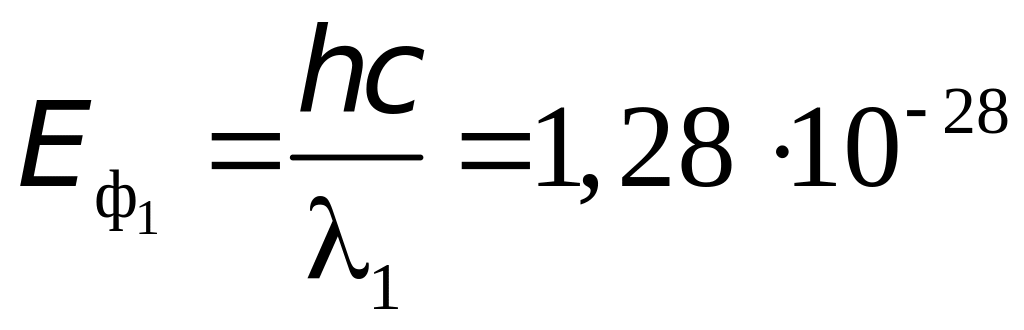Дж = 8 эВ,

что много меньше энергии покоя электрона . Поэтому максимальная кинетическая энергия фотоэлектрона выражается по классической формуле из уравнения Эйнштейна , и равна

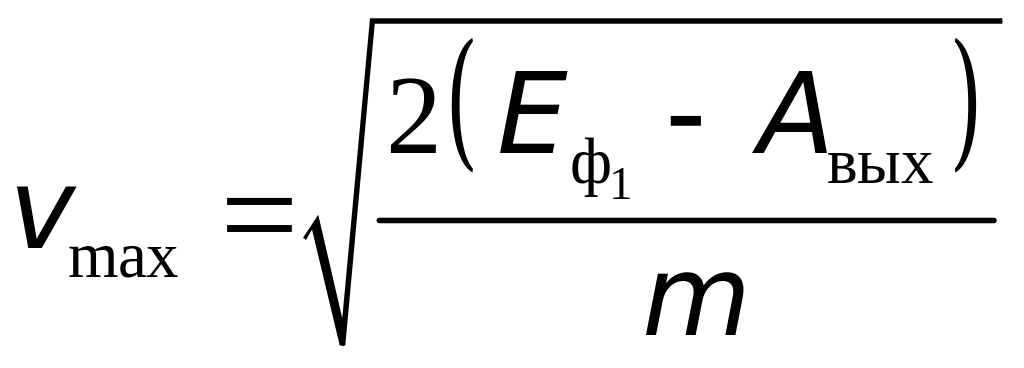=1,0810⁶м/с.

2. Энергия фотона  - излучения 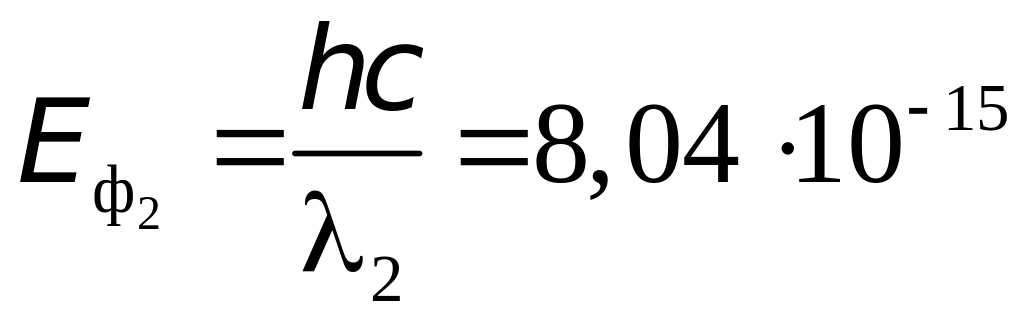Дж = 0,502 МэВ

сравнима с энергией покоя электрона, поэтому для вычисления его кинетической энергии необходимо использовать релятивистскую формулу. Работа выхода ( = 4,7 эВ) много меньше энергии  - фотона, поэтому ею можно пренебречь:

Выполнив преобразования, из уравнения Эйнштейна найдем

=0,755,

м/с.

Задача 2. Красная граница фотоэффекта для никеля равна 0,257 мкм. Найдите длину волны света, падающего на никелевый электрод, если фототок прекращается при задерживающей разности потенциалов, равной 1,5 В.

Решение. Найдем длину волны из уравнения Эйнштейна .

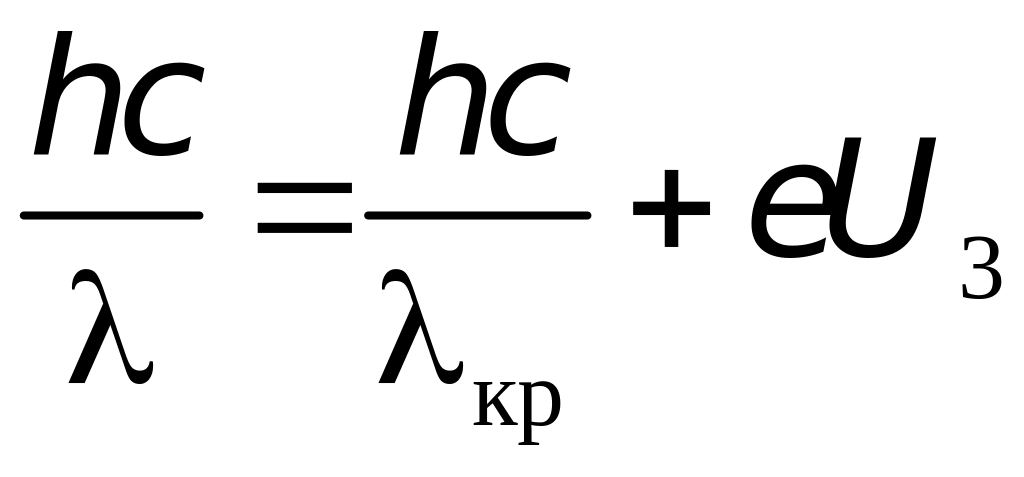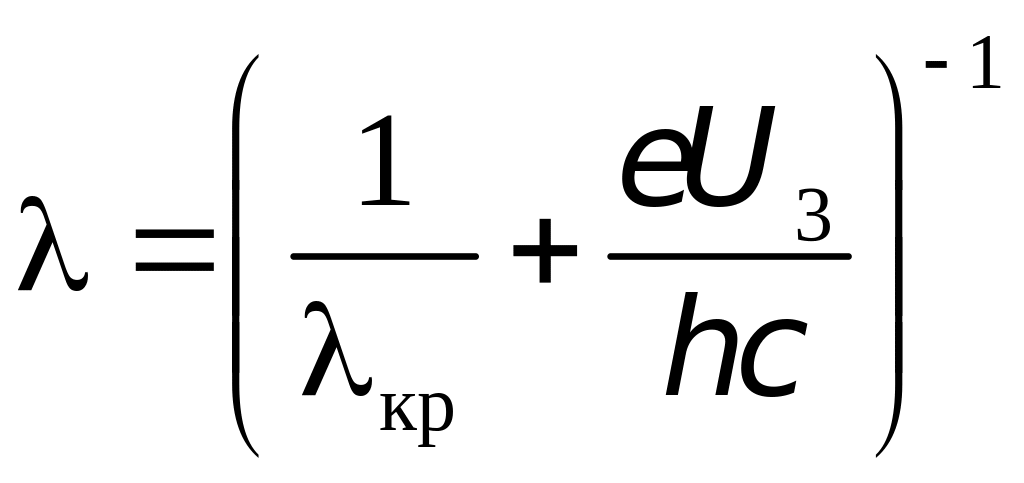= 196 нм.

Задача 3. Какую часть энергии фотона составляет энергия, которая пошла на совершение работы выхода электронов из металла, если длина волны для красной границы равна 0,54 мкм, а максимальная кинетическая энергия фотоэлектронов 0,5эВ?  

Решение. Из формулы Эйнштейна для фотоэффекта получим 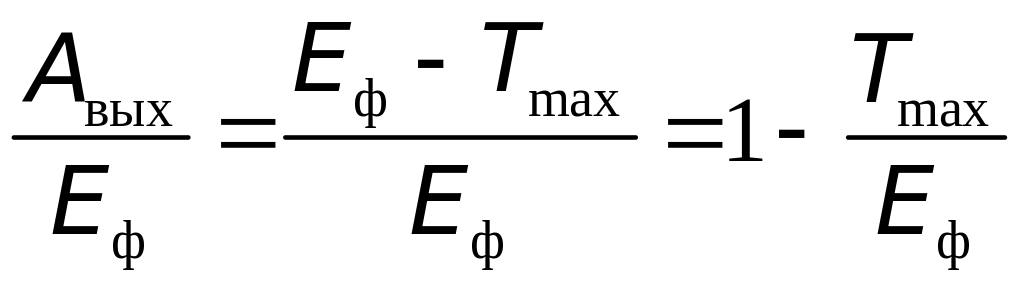, где 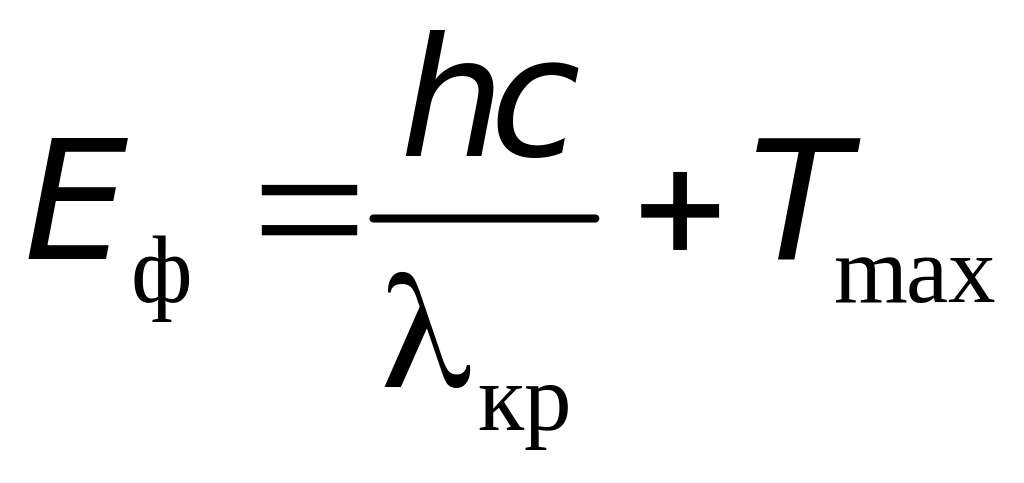= 4,4810^-19 Дж = 2,8 эВ.

Тогда , то есть составляет 82%.

Задача 4. Возникает ли фотоэффект в цинке под действием излучения, имеющего длину волны 0,45 мкм? Работа выхода электронов из цинка равна 4,2 эВ.

Решение. Минимальная энергия кванта, вызывающего фотоэффект, равна работе выхода. Энергия кванта по условию задачи равна 2,75 эВ, что меньше работы выхода. Поэтому фотоэффекта не будет.

Задача 5. Металлический шар радиусом 10 см облучают светом с длиной волны 200 нм. Определите установившийся заряд шара, если работа выхода электрона с его поверхности равна 7,210^–19 Дж.

Решение. На шаре установится такой заряд, что под действием его электростатического поля самые быстрые электроны, покидающие поверхность шара вследствие фотоэффекта, вернутся на положительно заряженный шар. В этом случае вы

полняется равенство , где 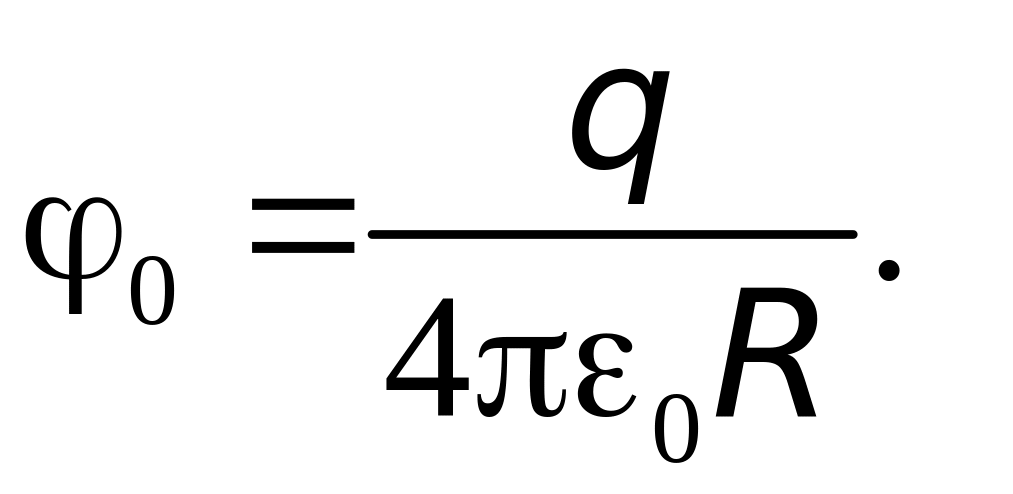Из уравнения Эйнштейна получим 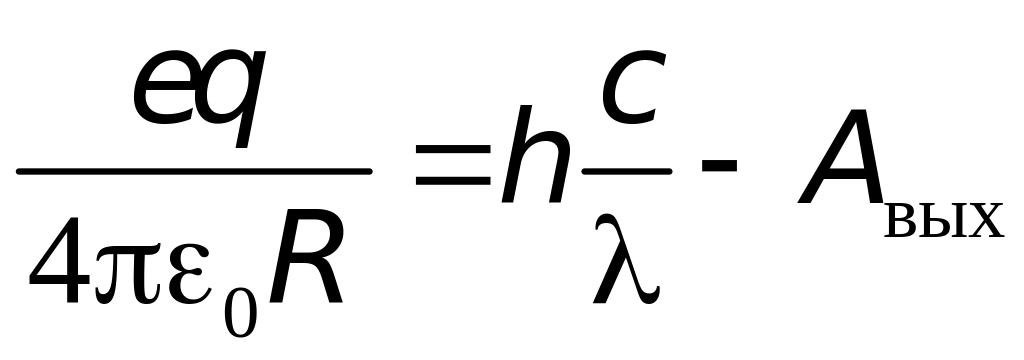, откуда

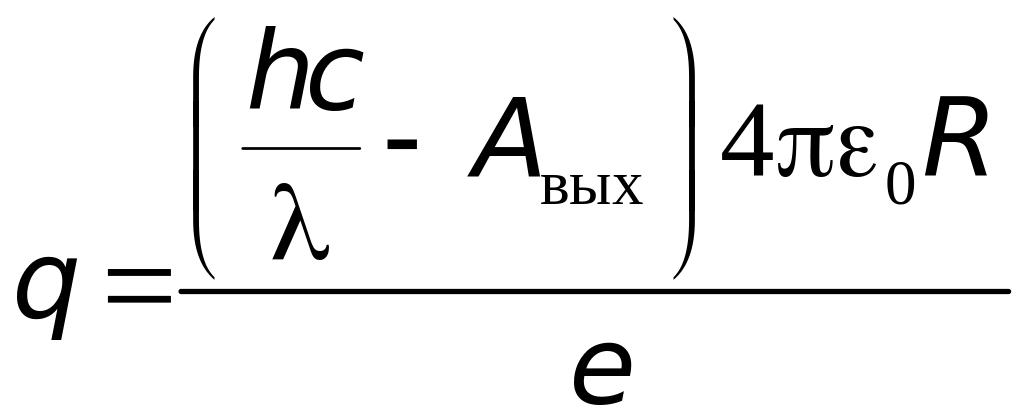= 1,910^–11 Кл.

Задача 6. Фотоны с длиной волны 330 нм вырывают электроны из металла с работой выхода 2,9 эВ. Найдите максимальный импульс, передаваемый поверхности металла при вылете каждого электрона в результате фотоэффекта. Считать, что электрон вылетает нормально к поверхности катода навстречу падающему фотону.

Решение. Закон сохранения импульса для фотоэффекта имеет вид (рис.6):

_,

фотокатод

Рис.6

где – импульс фотона, – максимальный импульс электрона, – импульс, полученный поверхностью катода. Из уравнения Эйнштейна импульс падающего фотона

.

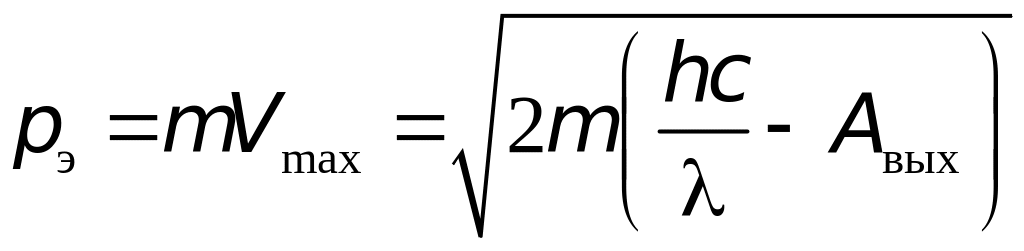Импульс, передаваемый поверхности, равен сумме импульса фотона и импульса вылетевшего фотоэлектрона.

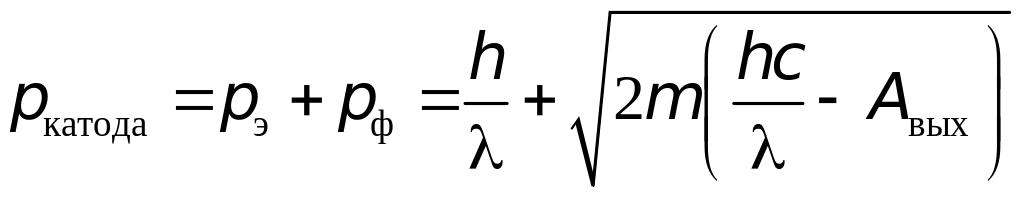= 510^–25 кгм/с.