25. Альфа –распад

Альфа–распад представляет собой самопроизвольный распад материнского

ядра , в результате которого испускается альфа–частица (ядро атома гелия) и образуется дочернее ядро с массовым числом на 4 единицы меньше и порядковым номером на 2 единицы меньше , где - начальное или материнское ядро, - конечное или дочернее ядро. Примером αраспада является следующий процесс

.

αраспад обычно сопровождается испусканием - лучей. Ядро претерпевает αраспад, если его энергия связи относительно этого процесса отрицательна (масса материнского ядра m_x больше масс αчастицы и дочернего ядра ):

Энергия вылетающей αчастицы составляет несколько МэВ, которая при пролете в воздухе расходуется на ионизацию атомов. Длина пробега составляет несколько см в воздухе и порядка 10^-2 мм в твердом теле (лист бумаги полностью задерживает αчастицы). Энергия, выделяющаяся в результате распада (энергия связи) распределяется между ядром гелия и дочерним ядром. Кинетическая энергия αчастицы зависит от того, в каком энергетическом состоянии образуется дочернее ядро. Если оно находится в возбужденном состоянии, то переход в основное состояние происходит с испусканием  фотона. Энергия возбужденного состояния дочернего ядра может сняться испусканием протона, нейтрона, электрона, αчастицы. Возможна также внутренняя конверсия – прямое (без излучения) испускание электрона из K, L, M оболочек. Освободившееся место будет занято другим электроном с испусканием рентгеновского кванта.

αчастица возникает в ядре в момент распада и должна преодолеть потенциальный барьер (Рис.40), внутренняя сторона которого обусловлена ядерными силами, а внешняя кулоновским отталкиванием αчастицы и дочернего ядра. Кинетическая энергия αчастицы оказывается меньше высоты барьера, поэтому проникновение в область за барьером объясняется туннельным эффектом. Он заключается в том, что решение уравнения Шредингера для движения αчастицы в поле ядра дает отличную от нуля вероятность ее нахождения за потенциальным барьером – областью, которая запрещена для движения частицы в классической физике.

Рис.40 Схема туннельного эффекта при αраспаде

26. Бета–распад

Бета–распад – процесс превращения нестабильного ядра в ядро - изобару с порядковым номером, отличным от исходного на ΔZ = ±1, сопровождаемый испусканием электрона (^ -распад), или позитрона (^ -распад). Одновременно ядро испускает нейтрино или антинейтрино . К -распадам относят также электронный захват – захват электрона ядром с испусканием нейтрино.

^ -распад происходит по схеме + , например,

+ .

Ядро претерпевает ^распад, если его энергия связи относительно этого распада отрицательна (масса материнского ядра больше масс дочернего ядра и электрона m_e ):

Простейший ^ -распад – распад свободного нейтрона:

+ .

В этом процессе внутри ядра рождается электрон и антинейтрино. ^-распад может сопровождаться подобно αраспаду излучением при переходе дочернего ядра из возбужденного состояния в основное. Распределение электронов по энергиям (энергетический спектр) имеет вид (Рис.41)

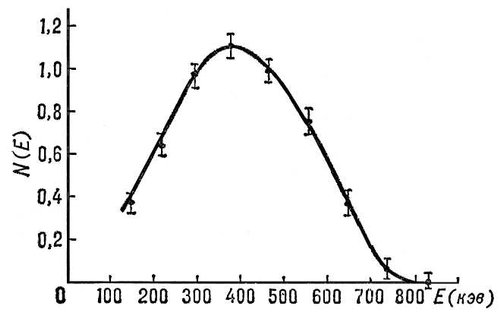
Рис.41 Энергетический спектр электронов, рождающихся при ^-распаде. E – энергия электрона, N(E) – число электронов с энергией E.

Предполагалось, что при ^-распаде электроны должны вылетать с одной кинетической энергией соответствующей разности энергии материнского ядра и дочернего ядра вместе с электроном (максимальная кинетическая энергия электронов 800 кэВ на рисунке). Непрерывный характер спектра электронов говорит о том, что электроны вылетают с меньшей энергией, чем та, которую определяет закон сохранения энергии, в котором некоторые физики стали сомневаться. Объяснить непрерывный спектр удалось, предположив, что вместе с электроном рождается еще одна частица, названная нейтрино (по-итальянски, «нейтрончик»). Энергия связи, освобождаемая при распаде, распределяется между электроном и нейтрино каждый раз по-разному. Это позволило понять, почему при ^распаде, как казалось, не выполнялся закон сохранения спина. При распаде нейтрона на протон и электрон начальный спин ½ не равен сумме спинов справа (целое число). При учете спина нейтрино ½ закон сохранения спина выполняется.

Эксперимент по прямому детектированию нейтрино впервые был осуществлен в 1953 в США Ф. Райнесом и К. Коуэном на реакторе в Хэнфорде. Спин нейтрино равен ½, а электрический заряд равен нулю. Масса покоя электронного нейтрино по современным данным не превышает 10 эВ, а возможно и много меньше

1 эВ

–распад происходит по схеме + , например,

.

Частица , аналогичная электрону, но с противоположным по знаку электрическим зарядом, получила название позитрон. Процесс – распада протекает так, как если бы протон в ядре превратился в нейтрон (свободный протон – стабильная частица):

распад происходит в случае, если энергия связи ядра относительно этого распада отрицательна (масса материнского ядра больше масс дочернего ядра и позитрона m_+e ):

Электронный захват происходит по следующей схеме

Ядро поглощает K, реже L, M электрон, например,

Процесс эквивалентен преобразованию в ядре протона в нейтрон

Электронный захват возможен, если сумма энергий материнского ядра и электрона m_e больше энергии дочернего ядра

Гамма- излучение и его взаимодействие с веществом

-излучение не является самостоятельным видом радиоактивности, а лишь

сопровождает - и  - распады, а также возникает при ядерных реакциях, при торможении заряженных частиц, их распаде и т. д. -спектр является линейчатым (дискретным), что является доказательством дискретности энергетических состояний атомных ядер.

-квант испускается дочерним (а не материнским) ядром, которое образуется в возбужденном состоянии. За время жизни этого состояния (10^-13- 10^-14 с) ядро переходит в основное состояние с испусканием -кванта. Переходя в основное состояние, возбужденное ядро может пройти через ряд промежуточных состояний, поэтому -излучение одного и того же радиоактивного изотопа может содержать несколько групп у-квантов с разной энергией.

-излучение большинства ядер является столь коротковолновым (с длиной волны  < 5·10⁻³ нм), что его волновые свойства проявляются очень слабо и на первый план выступают корпускулярные свойства. Поэтому -излучение рассматривают как поток -квантов с энергией в диапазоне от ~1 кэВ до десятков МэВ. При взаимодействии - излучения с веществом в зависимости от его энергии происходят следующие процессы.

При энергиях меньших 1 Мэв наблюдаются эффект Комптона и фотоэффект.

Если E_ 2m_ec²=1,022 МэВ (m_ec² – энергия покоя электрона), то в поле ядра происходит образование электрон-позитронной пары. Фотон с энергией, превышающей удвоенную энергию покоя электрона 2m₀с² = 1,022 МэВ, может образовать в поле ядра электронно-позитронную пару. Электронно-позитронная пара может быть также образована и в поле атомного электрона. Однако вероятность этого процесса примерно в Z раз меньше, чем образование пары в поле ядра. При энергиях E_МэВ - излучение вызывает ядерные реакции.

Интенсивность пучка монохроматических гамма–лучей, прошедших сквозь слой вещества толщиной , уменьшается по закону: , где – интенсивность излучения, падающего на слой; –линейный коэффициент ослабления.

Ядерные реакции

Символическая запись ядерной реакции: или ,

где и  –исходное и конечное ядра соответственно с зарядовыми числами и и массовыми числами и ; и - соответственно бомбардирующая и испускаемая (или испускаемые) в ядерной реакции частицы.

Для обозначения частиц приняты следующие символы: - протон, - нейтрон, - дейтон, - тритон,  – альфа–частица,  – гамма–квант.

Законы сохранения в ядерных реакциях:

А) числа нуклонов ;

Б) заряда ;

В) релятивистской полной энергии ;

Г) импульса .

Если общее число ядер и частиц, образовавшихся в результате реакции, больше двух, то запись соответственно дополняется. Энергия ядерной реакции , где и - массы покоя ядра–мишени и бомбардирующей частицы; ( ) - сумма масс покоя ядер продуктов реакции.

Если ( )( ), то энергия освобождается, энергетический эффект положителен, реакция экзотермическая.

Если ( )<( ), то энергия поглощается, энергетический эффект отрицателен, реакция эндотермическая.

Энергия ядерной реакции представляется также в виде: , где - соответственно кинетические энергии ядра–мишени, бомбардирующей частицы, испускаемой частицы и ядра продукта реакции.

Пороговая (минимальная) кинетическая энергия налетающей частицы, при которой становится возможной эндотермическая ядерная реакция: , где и - массы налетающей частицы и ядра мишени, - энергия реакции.

Примеры решения задач

Задача 1. Оцените плотность вещества в атомных ядрах.

Решение. Радиус ядра с массовым числом определяется формулой

,

где Ф - ферми – название применяемой в ядерной физике единицы длины, равной одному фемтометру (1 фм = 10^-15 м). Объем ядра:

м³.

Если пренебречь различием масс протона и нейтрона, то массу ядра можно определить по формуле

кг

Поэтому средняя плотность ядерного вещества

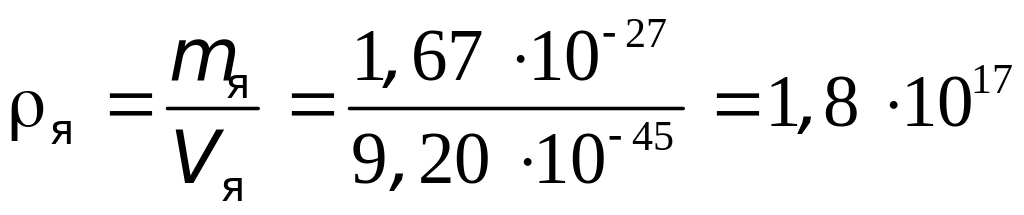кг/м³ .

Задача 2. Вычислите дефект массы и энергию связи ядра .

Решение. Дефект массы ядра можно определить из соотношения:

, где - зарядовое число, А – массовое число, - масса атома водорода, - масса нейтрона, - масса атома бора.

Подставляя табличные значения этих величин, получим:

а.е.м., или а.е.м.

Энергия связи ядра определяется соотношением =76,2 МэВ.

Задача 3. Определите удельную энергию связи ядра .

Решение. В литии на один нуклон приходится энергия связи, равная:

.

Подставляя табличные значения величин, получим:

МэВ/нуклон = 5,61 МэВ/нуклон.

Задача 4. Определите зарядовое число и массовое число частицы, обозначенное буквой , в символической записи ядерной реакции:

1) ;

2) ;

3) .

Решение. Для нахождения в записанных реакциях зарядового числа и массового числа воспользуемся законами сохранения зарядовых и массовых чисел:

1) ; (нейтрон)

2) ; (нейтрон)

3) ; (протон)

Задача 5. Найдите среднее время жизни радиоактивного вещества , если его активность уменьшается на за время = 60 минут.

Решение. Активность уменьшается со временем по закону радиоактивного распада .

Уменьшение активности определяется соотношением:

.

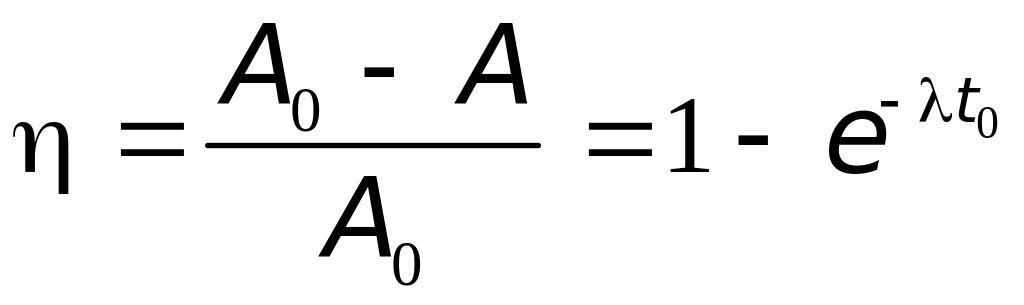Постоянная распада  связана со средним временем жизни ядра: , откуда

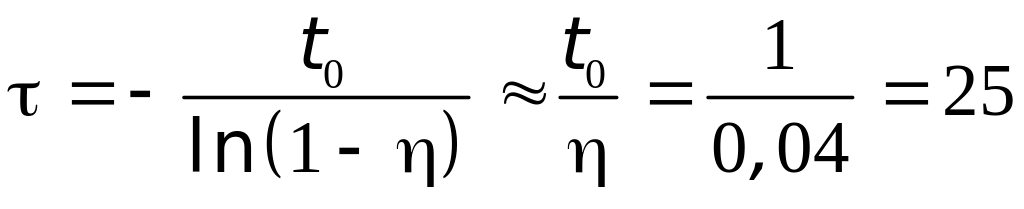часов.

Задача 6. За год распалось 60% некоторого исходного радиоактивного элемента. Определите его период полураспада.

Решение. В соответствии с законом радиоактивного распада отношение числа расраспавшихся ядер к числу нераспавшихся имеет вид:

.

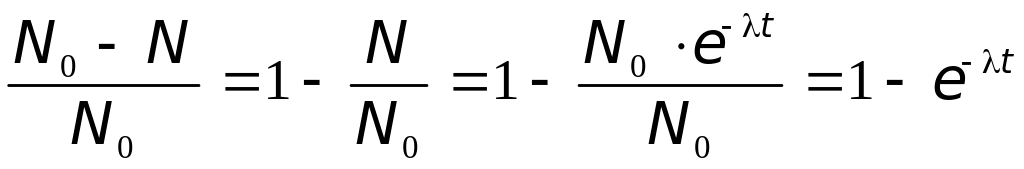По условию задачи это отношение равно 0,6, откуда 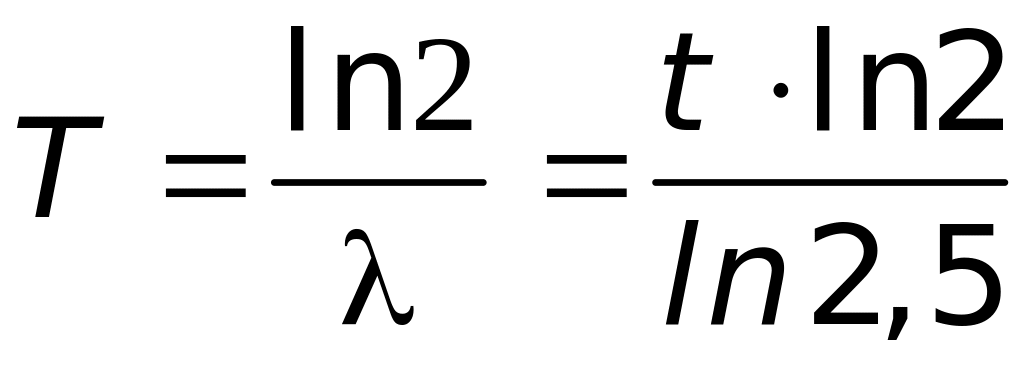= 0,76 года.

Задача 7. Вычислите энергию ядерной реакции . Выделяется или поглощается энергия при этой реакции?

Решение. Энергия ядерной реакции определяется по формуле:

,

где и - массы частиц, вступающих в реакцию, - сумма масс частиц, образовавшихся в результате реакции.

Вычисляя, получим для пороговой энергии этой реакции

= –0,0184 а.е.м., = –17,4 МэВ